DFS and BFS

Create Graph

networkx tutorial

In [1]:

import random, sys, copy
import numpy as np
import networkx as nx
from collections import defaultdict
from collections import deque
from networkx.drawing.nx_pylab import draw_networkx
from IPython.display import HTML
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
# %matplotlib inline

In [2]:

# a randomly generated graph 
g = nx.DiGraph()
n, edges = 10, []
g.add_nodes_from(list(range(n)))
for i in range(n):
    k = random.randint(0, (1 + n) // 4) # vertex 하나당 outgoing edge수 결정
    edges.extend([(i, int(np.random.choice(list(range(i)) + list(range(i+1,n)), size=None))) for _ in range(k)])
g.add_edges_from(edges)
# make g as a circular structure 
pos = nx.circular_layout(g)

In [3]:

draw_networkx(g, pos=pos, with_label=True, width=2.0, alpha=0.8)
plt.savefig("path.png")

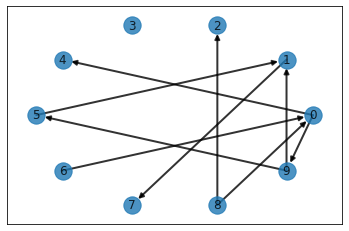
In [4]:

g.nodes()

NodeView((0, 1, 2, 3, 4, 5, 6, 7, 8, 9))

In [5]:

g.edges()

OutEdgeView([(0, 4), (0, 9), (1, 7), (5, 1), (6, 0), (8, 0), (8, 2), (9, 1), (9, 5)])

Viusalization Helper

Later, we will visualize how to operate DFS and BFS using below functions.

In [6]:

def plotframe(frame):
    edges, grays, blacks = frame['edges'], frame['grays'], frame['blacks']
    nx.draw_networkx(g, pos=pos, with_labels=True, width=1.0, font_color='w')  
    nx.draw_networkx_edges(g, pos=pos, edgelist=edges, width=2.0, edge_color='r')
    nx.draw_networkx_nodes(g, pos=pos, nodelist=grays, node_color='gray')
    nx.draw_networkx_nodes(g, pos=pos, nodelist=blacks, node_color='black')

def updateframe(frames, gray=[], black=[], edge=[]):
    frame = copy.deepcopy(frames[-1])
    frame['grays'].extend(gray)
    frame['blacks'].extend(black)
    frame['edges'].extend(edge)
    frames.append(frame)

DFS

GeeksforGeeks

Implementation

In [7]:

frames = [defaultdict(list)]

def DFS(g):
    seen = defaultdict()
    finish = []
    def util(u):
        """ recursive """
        # similar with u = stack.pop()
        # visiting time, mark this node, that is, update u.d.
        # note that not marking as soon as going inside
        seen[u] = True
        print(u, end=' ')
        updateframe(frames, gray=[u])
        
        for v in g.adj[u]:
            if v not in seen:
                # calling time, not marking before going inside
                updateframe(frames, edge=[(u, v)])
                util(v)
        
        # finishing time, set u.f.
        finish.append(u)
        updateframe(frames, black=[u])
        return 
    
    # calling time, not marking before going inside
    # util(2) # 2 0 1 3
    for s in g.nodes():
        if s not in seen:
            util(s) # starts at s.
    print(finish), finish.clear()
    print(), seen.clear()
    
    # iterative 
    def util_v2(s):
        """ iterative """
        seen[s] = True
        stack = [s]
        while stack != []:
            u = stack.pop()
            # visiting time, mark this node, and update u.d.
            # note that not marking as soon as going inside
            # == not marking as soon as pop from stack.
            seen[u] = True
            print(u, end = ' ')
            
            for v in g.adj[u]:
                if v not in seen:
                    # calling time, not marking before going inside 
                    # == not marking before append into stack.
                    stack.append(v)
            # finishing time cannot be found when we use the iterative way.
        return 
        
    util_v2(2)
    # for s in g.nodes():
    #     if s not in seen:
    #        util(s) # starts at s.

DFS(g)

0 4 9 1 7 5 2 3 6 8 [4, 7, 1, 5, 9, 0, 2, 3, 6, 8]

2 

Visualization

In [8]:

f, axes = plt.subplots()
ani = FuncAnimation(
        fig=f, func=plotframe,
        frames=frames, 
        blit=False, interval=1000) # True일 경우 update function에서 artist object를 반환해야 함

HTML(ani.to_html5_video())

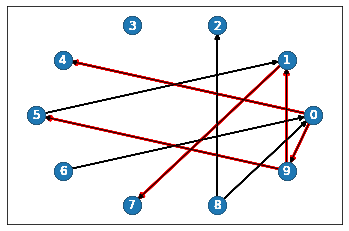
If you see an <>Error related to ffmpeg
$ sudo apt install ffmpeg

Report

• 함수에 들어간 뒤에 marking 하는것을 기억하자.
• visit하는 것은 함수에서 들어간 직후이며 marking을 할때와 동일한 시기이다.
• finishing time은 갈 수 있는 끝까지 갔을때 더이상 갈 노드가 없으면 끝이난다. 나중에, Topological sort에 이용
• adj list에 대해 방문순서에 따라 다르게 출력된다.
• iterative 방식과 recursive 방식이 있다.

시간은 모든 vertex들과 edege들을 한번씩보게 되므로, $O(|V|+|E|)$

Note

iterative방식을 사용할경우 finishing time을 찾는것은 불가능

BFS

GeeksforGeeks

In [9]:

frames = [defaultdict(list)]

def BFS(g):
    seen = defaultdict()
    finish = []
    def util(s):
        
        queue = deque([s])
        seen[s] = True
        updateframe(frames, gray=[s])
        
        while queue:
            u = queue.popleft()
            # visiting time, update u.d.
            print(u, end=' ')
            updateframe(frames, gray=[u])
            
            for v in g.adj[u]:
                if v not in seen:
                    # note that marking before going inside
                    seen[v] = True
                    queue.append(v)
                    updateframe(frames, edge=[(u, v)])
            
            # finishing time, set u.f.
            finish.append(u)
            updateframe(frames, black=[u])
    # util(2)
    for s in g.nodes():
        if s not in seen:
            util(s) # starts at s.
    print(finish)
        
BFS(g)   

0 4 9 1 5 7 2 3 6 8 [0, 4, 9, 1, 5, 7, 2, 3, 6, 8]

Visualization

In [10]:

f, axes = plt.subplots()
ani = FuncAnimation(
        fig=f, func=plotframe,
        frames=frames, 
        blit=False, interval=1000) # True일 경우 update function에서 artist object를 반환해야 함

HTML(ani.to_html5_video())

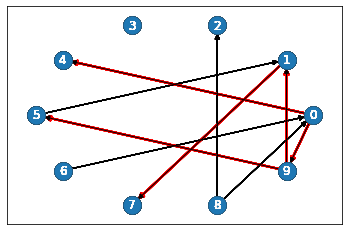
Report

• queue에 들어가기 전에 marking 하는것을 기억하자.
• visit하는 것은 queue에서 나온 직후이며 marking을 할때와 다른 시기이다.
• finishing time은 한 노드에서 이웃된 자신의 level + 1 노드들의 모든정보를 queue에 올리면 끝이 나는 시기이다.
• adj list에 대해 방문순서에 따라 다르게 출력된다.
• iterative 방식과 recursive 방식이 있다.

시간은 모든 vertex들과 edege들을 한번씩보게 되므로, \(O(|V|+|E|)\)

Note

queue를 사용하므로 stack방식인 recursive방식으로는 구현하기 까다롭다. blog