2D Cloest Pair python (Divide and Conquer)

Closest Pair of Points

geeksforgeeks

Configuration

In [1]:

import sys
import numpy as np
import random, math
import logging, argparse, yaml, copy
import matplotlib.pyplot as plt
from utils.verbose import logging_time
from collections import deque

MAX = 1e10

SEED = 0
np.random.seed(seed=SEED)
random.seed(SEED)

VERBOSE = True
# setup logging
logging.basicConfig(
    format="%(asctime)s - %(message)s",
    datefmt="%m/%d/%Y %H:%M:%S",
    level=logging.INFO if VERBOSE else logging.WARNING)

Naive

Enumerate all pair distance, and take the minimum value.

\[T(n) = O(n^2)\]

In [2]:

def distance(a, b):
    """ get distance between 2 points. """
    return math.sqrt((a[0] - b[0]) ** 2 + (a[1] - b[1]) ** 2)

@logging_time
def cloest_naive(points):
    """ find minimum distance from enumerating all cases. """
    ans = MAX
    size = len(points)
    for i in range(size):
        for j in range(i+1, size):
            ans = min(ans, distance(points[i], points[j]))
    return ans

In [3]:

points = [(-4, 4), (-3, 2), (-2, -1), (-1.5, 4), (-1, -2), (0, 1), (1.5, 2), (2, 4), (3, 2), (3, 0), (4, 3), (4, -2)]
ans, _ = cloest_naive(points)
ans

1.4142135623730951

Divide Conquer

We can improve 2D Closest pair of points algorithm using Divide and Conquer technique.

Key idea

1. find mid point in linear time.
2. get minimum distances of left, right recursively.
3. find cross minimum distance in linear time, and then return min(left, right, cross)

Therefore, if we take linear time quick selection algorithm in order to get mid point index, the time complexity is as follows. \(T(n) = 2T(n/2) + O(n) = O(nlogn)\)

Find mid point in linear time, and get minimum distances of left and right recursively.

In order to do that, we have to use linear time mid point selection algorithm based on median of medians algorithm.
The detail algorithm is described at this post.
Note that we have to transform the linear time selection algorithm to be operated by index, instead of ordered statistic.

To simplify this algorithm, I used randomized quick select algorithm, instead of linear time quick select algorithm.
The overhead of randomized quick select algoritm, the worst case time complexity becomes $O(n^2)$.
However, the average time is $O(n)$

Recursively find minimum distances of left and right part as follows.

In [4]:

def partition(points, s, e, axis=0, verbose=False):
    """ randomized partition by axis
    points[i+1] finds the right place. """
    i = np.random.randint(s, e + 1)
    points[i], points[e] = points[e], points[i]
    pivot = points[e][axis]
    if verbose: print("{} is a pivot".format(points[e]))
    i = s - 1
    for j in range(s, e):
        if points[j][axis] <= pivot:
            i += 1
            points[i], points[j] = points[j], points[i]
    points[i + 1], points[e] = points[e], points[i + 1]
    return i + 1

def quick_select(points, s, e, k, axis=0):
    """ find the k-th smallest index of points by axis.
    please note that this algorithm returns `index`. """
    assert (not s > e) and (k >= 0), "index error!"
    if s == e: return e
    # q is pivot index
    q = partition(points, s, e, axis=axis)
    if k < q:
        return quick_select(points, s, q - 1, k, axis=axis)
    elif k == q:
        return q
    else:
        return quick_select(points, q + 1, e, k, axis=axis)

In [5]:

# check
for SEED in range(5):
    np.random.seed(seed=SEED)
    random.seed(SEED)
    sizes = list(range(5, 10, 10))
    for i, size in enumerate(sizes):
        points = [np.random.randint(-5 * size, 5 * size, size=2).tolist() for i in range(size)]
        # logging.info(points)
        q = partition(points, 0, size - 1, axis=0, verbose=False)
        logging.info("after partition ...")
        logging.info(points)
        logging.info("points[{}] = {}".format(q, points[q]))

03/12/2020 05:40:30 - after partition ...
03/12/2020 05:40:30 - [[-4, 11], [-25, -22], [-22, 14], [-16, -6], [19, 22]]
03/12/2020 05:40:30 - points[4] = [19, 22]
03/12/2020 05:40:30 - after partition ...
03/12/2020 05:40:30 - [[-25, -9], [-16, -14], [-20, -10], [-13, -17], [12, 18]]
03/12/2020 05:40:30 - points[3] = [-13, -17]
03/12/2020 05:40:30 - after partition ...
03/12/2020 05:40:30 - [[-7, -14], [-3, 18], [15, -18], [15, -10], [20, -17]]
03/12/2020 05:40:30 - points[1] = [-3, 18]
03/12/2020 05:40:30 - after partition ...
03/12/2020 05:40:30 - [[-25, -4], [-22, -17], [18, 16], [-6, -15], [17, -1]]
03/12/2020 05:40:30 - points[0] = [-25, -4]
03/12/2020 05:40:30 - after partition ...
03/12/2020 05:40:30 - [[-24, 15], [20, 5], [-2, -17], [-16, 14], [21, -20]]
03/12/2020 05:40:30 - points[0] = [-24, 15]

In [6]:

k = 2
logging.info("after select (point order changed) ... ")
logging.info("points[{}] is the {}-th smallest point".format(quick_select(points, 0, size - 1, k), k))
logging.info(points)

03/12/2020 05:40:30 - after select (point order changed) ... 
03/12/2020 05:40:30 - points[2] is the 2-th smallest point
03/12/2020 05:40:30 - [[-24, 15], [-16, 14], [-2, -17], [20, 5], [21, -20]]

In [7]:

# sanity check
for SEED in range(10):
    np.random.seed(seed=SEED)
    random.seed(SEED)
    sizes = list(range(1, 300, 10))
    for i, size in enumerate(sizes):
        """ generate 2D points within 10*size square. """
        points = [np.random.randint(-5 * size, 5 * size, size=2).tolist() for i in range(size)]
        test = copy.deepcopy(points)
        k = random.randint(0, size-1)
        i = quick_select(points, 0, size-1, k)
        pred = points[i]
        ans = sorted(test, key=lambda p: p[0])[k]
        # print("{}-th smallest point: {}.x == {}.x".format(k, pred, ans))
        assert pred[0] == ans[0]

Find cross minimum distance to compare with left and right cases.

Assume that the algorithm takes left, right minimum distances recursively.
Let min(left, right) be d.

cross-minimum distance can be found by enumerating all pair distance in left and right points.
However, it takes $O(n/2 \times n/2) = O(n^2)$. This way does not improve naive case.

In [8]:

def find_cross_min(points, s, q, e, recur_min, axis=0):
    """ find cross minimum distance from points[s:e+1]
    note that we already know
        points[q] is strictly larger than points[s:q]
        points[q] is strictly smaller than points[q+1:e]
    """
    left = []
    for i in range(s, q + 1):
        if points[q][axis] - points[i][axis] <= recur_min:
            left.append(points[i])

    right = []
    for i in range(q + 1, e + 1):
        if points[i][axis] - points[q][axis] <= recur_min:
            right.append(points[i])

    cross_min = MAX
    for p_l in left:
        for p_r in right:
            cross_min = min(cross_min, distance(p_l, p_r))
    return cross_min

In [9]:

@logging_time
def closest_recursive(points, s, e, axis=0):
    return closest(points, s, e, axis)

def closest(points, s, e, axis=0):
    """ find minimum distance from divide and conquer."""
    assert not (s > e), "index error!"
    # base cases
    if s == e: # self-distance is MAX.
        return MAX
    if e - s == 1:
        return distance(points[s], points[e])

    mid = (s + e) // 2
    q = quick_select(points, s, e, mid, axis=axis)

    # find minimum distance at each partition.
    left = closest(points, s, q, axis=axis)
    right = closest(points, q + 1, e, axis=axis)
    recur_min = min(left, right)
    cross_min = find_cross_min(points, s, q, e, recur_min, axis=axis)
    return min(recur_min, cross_min)

In [10]:

SEED = 0
np.random.seed(seed=SEED)
random.seed(SEED)
sizes = list(range(10, 1000, 50))
t1, t2 = [0] * len(sizes), [0] * len(sizes)
for i, size in enumerate(sizes):
    """ generate 2D points within 10*size square. """
    points = [np.random.randint(-5 * size, 5 * size, size=2).tolist() for i in range(size)]
    ans1, t1[i] = closest_recursive(points, 0, size - 1, axis=0)
    ans2, t2[i] = cloest_naive(points)
    assert ans1 == ans2

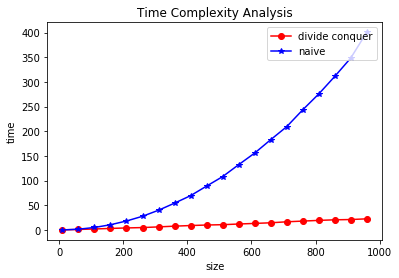
plt.xlabel('size')
plt.ylabel('time')
plt.title("Time Complexity Analysis")
plt.plot(sizes, t1, 'o-r', label="divide conquer")
plt.plot(sizes, t2, '*-b', label='naive')
plt.legend(loc='upper right')
plt.show()

How can we find cross-minimum distance in linear time?

Please note that following facts.

1. The points are partitioned by mid-point along the axis-x since the algorithm uses a quick selection algorithm by axis-x.
   

2. We already know d=min(left, right), so pruning can be possible by only seeing points within the strip.
   

3. There are up to 6 points on the opposite side with a distance less than the minimum distance.
   

Therefore, it takes O(6n/2) = O(n)

This is because we get left-minimum and right-minimun distances recursively.
There are no pairs within the (left or right) part where the distance is less than the minimum (left, right).

Therefore, it can be poosible to find cross-minimum distacne in linear time.
However, merging points by another axis-y is necessary to remove candidates with six candidates in addition to partitioning by axis-x.

In [11]:

def merge(points, s, q, e):
    """ sort by merging pre-sorted left and right along one axis. """
    n1 = q - s + 1
    n2 = e - q
    L, R = [], []
    for i in range(n1):    # L[0.. n1-1] <- A[p..q] 
        L.append(points[s + i])  
    for j in range(n2):
        R.append(points[q + j + 1])  # R[0.. n2-1] <- A[q+1..r]
    L.append([-MAX, -MAX])
    R.append([-MAX, -MAX]) 
    i, j = 0, 0
    # merge L[i] and R[j] in order to sort A[p.. q]
    for k in range(s, e + 1):
        if L[i][1] >= R[j][1]:
            points[k] = L[i]
            i += 1
        else: 
            points[k] = R[j]
            j += 1 
            
def merge_sort(points, s, e):  # A[p..r]까지 sorting 
    if s >= e: return    
    q = (s + e) // 2     
    merge_sort(points, s, q)
    merge_sort(points, q + 1, e)
    merge(points, s, q, e)

In [12]:

for SEED in range(5):
    SEED = 0
    np.random.seed(seed=SEED)
    random.seed(SEED)
    sizes = list(range(10, 1000, 50))
    for i, size in enumerate(sizes):
        points = [np.random.randint(-5 * size, 5 * size, size=2).tolist() for i in range(size)]
        # logging.info(points)
        merge_sort(points, 0, size - 1)
        # logging.info("after sorting ...")
        assert points ==sorted(points, key=lambda p: p[1], reverse=True), "not sorted"
    print("pass")

pass
pass
pass
pass
pass

Note

Note that partitioned results will be changed if we call merge recursively.
In that, pivot posiiton is changed after recursion, so keep pivot of axis-x as qx.
Also, find_cross_min_v2 is improved mathmatically because we only search strip line at most 6 element per each point.

In [13]:

def find_cross_min_v2(points, s, q, e, d, qx):
    """ find cross minimum distance from points[s:e+1] 
    note that left and right sorted by axis-y. """
    # test = copy.deepcopy(points)
    # assert points[s:q+1] == sorted(test[s:q+1], key=lambda x: x[1], reverse=True), "{}".format(points[s:q+1])
    # assert points[q+1: e+1] == sorted(test[q+1: e+1], key=lambda x: x[1], reverse=True), "{}".format(points[q+1:e+1])
    
    # pruning point: keep only points within strip.
    left = [points[i] for i in range(s, q + 1) if abs(qx - points[i][0]) <= d]
    right = [points[i] for i in range(q + 1, e + 1) if abs(qx - points[i][0]) <= d]
    strip = copy.deepcopy(left + right)
    merge(strip, 0, len(left)-1, len(strip)-1) 
    
    cross = d
    for i in range(len(strip)-1):
        for j in range(i+1, min(i+7, len(strip))):
            cross = min(cross, distance(strip[i], strip[j]))
    return cross

In [14]:

@logging_time
def closest_recursive_v2(points, s, e):
    return closest_v2(points, s, e)

def closest_v2(points, s, e):
    """ find minimum distance from divide and conquer."""
    assert not (s > e), "index error!"
    # base cases
    if s == e: # self-distance is MAX.
        return MAX
    if e - s == 1: # merge for length 2 case.
        if points[s][1] < points[e][1]:
            points[s], points[e] = points[e], points[s]
        return distance(points[s], points[e])
    
    mid = (s + e) // 2
    q = quick_select(points, s, e, mid)
    # keep points[q] axis-x because points are sorted by y-axis after pass closest(..) merge
    qx = points[q][0]

    # find minimum distance at each partition.
    left = closest_v2(points, s, q)
    right = closest_v2(points, q + 1, e)
    recur_min = min(left, right)
    cross_min = find_cross_min_v2(points, s, q, e, recur_min, qx)
    merge(points, s, q, e) # this line is added
    return min(recur_min, cross_min)

In [15]:

for SEED in range(1):
    # SEED = random.randint(0, 100)
    np.random.seed(seed=SEED)
    random.seed(SEED)
    sizes = list(range(100, 2000, 100))
    t1, t2 = [0] * len(sizes), [0] * len(sizes)
    for i, size in enumerate(sizes):
        """ generate 2D points within 10*size square. """
        points = [np.random.randint(-5 * size, 5 * size, size=2).tolist() for i in range(size)]
        # ans, _ = cloest_naive(points)
        ans1, t1[i] = closest_recursive(points, 0, size - 1)
        ans2, t2[i] = closest_recursive_v2(points, 0, size - 1)
        # print(ans, ans1, ans2)
        assert ans1 == ans2, "{}, {} {}".format(ans1, ans2, points)

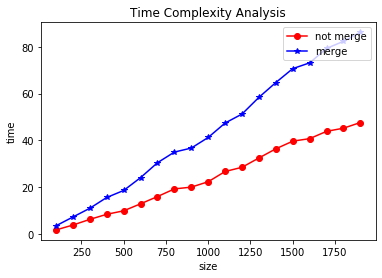
    plt.xlabel('size')
    plt.ylabel('time')
    plt.title("Time Complexity Analysis")
    plt.plot(sizes, t1, 'o-r', label="not merge")
    plt.plot(sizes, t2, '*-b', label="merge")
    plt.legend(loc='upper right')
    plt.show()

Reference:

blog