1
2
3
4
import networkx as nx
import matplotlib.pyplot as plt
from networkx.drawing.nx_pylab import draw_networkx
from collections import defaultdict
Disjoint Set(or Union Find)
서로 중복 되지 않는 부분 집합들. geeksforgeeks에 disjointset을 만드는 예제가 있다.
예를 들면, 사람 10명이 있고, 그중 친구관계들이 주어졌을때, disjoint set을 찾아라.
특징
- disjoint set has representative for each set
representative is a root that has parents as itself
ADT
n 개의 distinct 한 element들이 있다고 가정.
- MakeSet: 자기 자신을 representative로 하는 노드 생성. ($O(1)$)
- Find: parent를 recursive하게 찾아 root에 있는 representative return 함.(최악의 경우 $O(n)$ 연산)
- Union: Find에 의해 representative를 찾고, disjoint하다면 두 set을 합친다.(Find 시간에 비례, 최악의 경우 $O(n)$)
$m$ 은 DisjointSet을 구성하는데 필요한 모든 operation 수(make set, union, find 등).
$m \le 2n - 1$ 이다. $\because$ $n$ 번 makeset하고, 최악의 경우 union 을 $n - 1$ 번 해야하므로
따라서, DisjointSet을 구성하는데 걸리는 시간은 최악의 경우
- $n$번의 MakeSet, $O(n)$
- $n - 1$번의 Union, $O(n^2)$ $\because$ Find 연산의 최악의 경우 $O(n)$ \(O(n^2)\)
DisjointSet을 만드는 시간이 너무 오래걸린다.
Heuristic
It can be implemented by Linked List or Forests
I will use Forests using 2 heuristics.
- Union by rank: height(rank)에 따라 union (balanced tree로 만듦).
- Path compression: find 할때, representative를 $O(1)$에 곧바로 찾도록 한다.
Disjointset을 구성하는데 running time을
where $\alpha(n) \le 4$, $m$ is at most $2n - 1$ \(O(m\alpha(n))\)
로 향상 시켰다.
That is, it takes \(O(n)\) time approximately
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Treenode:
def __init__(self, nodename = 'unkown'):
self.d = 0
self.p = self
self.rank = 0
self.name = nodename
class DisjointSetForest:
def make_set(self, x):
x.p = x
x.rank = 0
def union(self, x, y):
self.link(self.find_set(x), self.find_set(y))
def link(self, x, y):
if x.rank > y.rank: # y 의 rank 가 x 보다 작으면, x를 y.p로 한다 (x가 representative가 됨)
y.p = x
else: # y 의 rank 가 x 같거나 크면, y를 x.p 로 한다. (이때 같다면 y를 representative 로 하고, y rank만 1증가)
x.p = y
if x.rank == y.rank:
y.rank = y.rank + 1
def find_set(self, x):
if x != x.p:
x.p = self.find_set(x.p)
return x.p
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
c = Treenode('c')
e = Treenode('e')
h = Treenode('h')
b = Treenode('b')
D = DisjointSetForest()
D.make_set(c)
D.make_set(e)
D.make_set(h)
D.make_set(b) # n = 4 make_set operation
print(c.rank, e.rank, c.p.name, e.p.name)
D.union(e,c)
print(c.rank, e.rank, c.p.name, e.p.name)
print(c.rank, e.rank, h.rank, c.p.name, e.p.name, h.p.name, c.name, e.name, h.name)
D.union(e,h)
print(c.rank, e.rank, h.rank, c.p.name, e.p.name, h.p.name, c.name, e.name, h.name)
D.union(e,b)
# at most n - 1 union operation
1
2
3
4
5
0 0 c e
1 0 c c
1 0 0 c c h c e h
1 0 0 c c c c e h
Efficient Implementation
dictionary 를 이용하여 더 효과적으로 구현해보자.
1
2
3
# toy example
people = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j'] # alphabets are distinct.
info = [['a', 'b'], ['b', 'd'], ['c', 'f'], ['c', 'i'], ['j', 'e'], ['g', 'j']]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
par = {}
rnk = {}
def find(x):
if not x in par:
par[x] = x # make set
rnk[x] = 0
return x
if x != par[x]:
par[x] = find(par[x]) # path compression
return par[x]
for e in people:
find(e)
print(par)
print(rnk)
def union(x, y):
x, y = find(x), find(y)
if x == y: return
if rnk[x] > rnk[y]: # union by rank
x, y = y, x
assert rnk[x] <= rnk[y], "{} > {}".format(rnk[x], rnk[y])
par[x] = y
if rnk[x] == rnk[y]:
rnk[y] += 1
for x,y in info:
union(x, y)
print(par)
print(rnk)
1
2
3
4
5
{'a': 'a', 'b': 'b', 'c': 'c', 'd': 'd', 'e': 'e', 'f': 'f', 'g': 'g', 'h': 'h', 'i': 'i', 'j': 'j'}
{'a': 0, 'b': 0, 'c': 0, 'd': 0, 'e': 0, 'f': 0, 'g': 0, 'h': 0, 'i': 0, 'j': 0}
{'a': 'b', 'b': 'b', 'c': 'f', 'd': 'b', 'e': 'e', 'f': 'f', 'g': 'e', 'h': 'h', 'i': 'f', 'j': 'e'}
{'a': 0, 'b': 1, 'c': 0, 'd': 0, 'e': 1, 'f': 1, 'g': 0, 'h': 0, 'i': 0, 'j': 0}
Visualization
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def visualize(par):
""" visualize disjoint set data structure. """
adj = defaultdict(list)
edges = []
for k, v in par.items():
adj[k].append(v)
edges.append((k, v))
print(adj)
g = nx.DiGraph()
g.add_edges_from(edges)
# pos = nx.circular_layout(g)
pos = nx.spring_layout(g, k=0.6)
draw_networkx(g, pos=pos, with_labels=True)
plt.show()
1
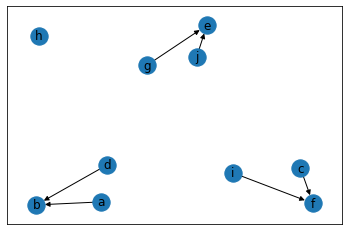
visualize(par)
1
2
defaultdict(<class 'list'>, {'a': ['b'], 'b': ['b'], 'c': ['f'], 'd': ['b'], 'e': ['e'], 'f': ['f'], 'g': ['e'], 'h': ['h'], 'i': ['f'], 'j': ['e']})
Practice
kakao 2019 intership test 에 좋은 연습 문제가 있다.
Key Idea
DisjointSet 을 사용하여 푼다.
각 disjoint 한 set이 representative 가
query로 들어온 방 번호보다 크며 남아있는 방중 가장 번호가 작은 값이 되도록
incremental 하게 disjoint set을 구성하면서 find을 통해 representative를 return하면 된다.
효율성을 통과하려면 주의해야할 사항이 3가지 있었다.(효율성에서 중요한 것은 시간, 메모리량이다.)
- union by rank를 쓰면 안된다.
일반적 disjointset과는 달리 representative가 남아있는 방중 가장 작은 번호가 되도록 union 해야하므로,
더 큰 값이 parent가 되도록 한다. (rank는 필요없다.) - 허용된 메모리량을 최대한 조금 써야한다.
list를 사용해서paraent를 관리할 경우,k값이 $10^{12}$ 까지 필요해서
list(range(10**12))를 할 경우 메모리 허용치가 초과된다. 따라서, dictionary를 이용하여parent를 관리해야한다. (c++ 의 경우 map 이용) - stack overflow 가 발생할 수 있다.
find를 recursive하게 동작하도록 구현했을 경우, stack이 넘쳐runtime error가 발생할 수 있다.1
sys.setrecursionlimit(10**6)
을 사용하여 허용치의 한계를 늘려야 했다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import sys
sys.setrecursionlimit(10**6)
def solution(k, room_number):
parent = {}
def find(x):
if not x in parent:
parent[x] = x
return x
if x != parent[x]:
parent[x] = find(parent[x])
return parent[x]
def union(x, y):
""" union x and y so that the larger one is the representative value. """
x, y = find(x), find(y)
if x == y: return
if x > y:
x, y = y, x
assert y >= x, "invalid"
parent[x] = y
ans = []
for want in room_number:
checkin = find(want)
assert checkin >= want, "checkin is the smallest among larger keys than want."
union(want, checkin + 1)
ans.append(checkin)
return ans
1
2
3
k = 10
room_number = [1, 3, 4, 1, 3, 1]
solution(k, room_number)
1
[1, 3, 4, 2, 5, 6]


Leave a comment