1
2
3
4
5
6
7
8
9
10
11
import random
import sys
sys.path.append("/home/swyoo/algorithm/")
from utils.verbose import logging_time
from sys import stdin
from copy import deepcopy
import matplotlib.pyplot as plt
import numpy as np
plot = lambda a: print(np.array(a))
stdin = open('data/dragon.txt')
input = stdin.readline
15685. 드래곤커브
Parse Data
1
2
3
n = int(input())
dragons = [list(map(int, input().split())) for _ in range(n)]
rotate = lambda i, j: (-j, i)
Idea:
회전시킨 k - 1 세대 드래곤 커브를 k - 1 커브에 이어붙혀 k 세대 드래곤 커브를 만든다.
문제를 주의 깊게 읽어야한다.
회전시키는 기준점은 드래곤 커브의 끝점인데 끝점은 커브를 따라 이동했을때 마지막 점을 의미한다.
그리고, 그 끝점에 이어 회전시킨 커브를 이어 붙힌다.
나의 실수
드래곤 커브를 회전시킬 때 끝점은 커브를 따라 이동했을때 마지막 점을 의미하는데, 나는 실수로 가장 먼거리에 있는 점으로 생각하여 잘못 풀었었다.그리고, 끝점을 알아내려면 커브를 끝는 순서를 따로 알 필요가 있어 points를 list로 가진 DFS 함수를 call한다.
맨 마지막 목표는 드래곤 커브의 점을 꼭지점으로 갖는 사각형을 갯수를 세는 것이므로,
커브의 순서를 알필요 없어서 points를 set으로 변경하였다.
규칙성 드래곤 커브를 이어붙힐때, 끝점부터 시작점까지 거꾸로 진행하며 회전시킨 선분을 이어붙히는 방식으로 구현하였다.
그런데 rebas’s blog 를 보면 이 규칙을 이용하여
iterative 하게 드래곤 커브를 1세대부터 10세대 까지 만들어 놓고, 이를 이용하여 답을 구하였다.
이렇게 계산하는게 더 빠를 것이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
def start(dir):
if dir == 0: return [(0, 0), (1, 0)]
if dir == 1: return [(0, 0), (0, -1)]
if dir == 2: return [(0, 0), (-1, 0)]
if dir == 3: return [(0, 0), (0, 1)]
def solution(dragons):
def dfs(cnt, points):
nonlocal aggre, g, x, y
if cnt == g:
points = set(map(lambda ij: (ij[0] + x, ij[1] + y), points))
aggre = aggre.union(points)
return
tmp, p = 0, None
for i, j in points:
dist = i ** 2 + j ** 2
if tmp < dist: tmp, p = dist, (i, j)
a, b = rotate(*p)
new = deepcopy(points)
for ij in points:
(i, j) = rotate(*ij)
new.add((i - a + p[0], j - b + p[1]))
dfs(cnt + 1, new)
aggre = set()
for x, y, d, g in dragons:
dfs(cnt=0, points=set(start(d)))
# print(sorted(aggre))
ans = 0
for i in range(100):
for j in range(100):
if all (True if (x, y) in aggre else False for x, y in [(i, j), (i + 1, j), (i, j + 1), (i + 1, j + 1)]):
ans += 1
return ans
print(solution(dragons))
1
2
1492
MyCode vs Another
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
@logging_time
def solution(dragons, show=False):
rotate = lambda i, j: (-j, i)
def start(dir):
if dir == 0: return [(0, 0), (1, 0)]
if dir == 1: return [(0, 0), (0, -1)]
if dir == 2: return [(0, 0), (-1, 0)]
if dir == 3: return [(0, 0), (0, 1)]
stores = []
def dfs(cnt, points):
nonlocal aggre, g, x, y
if cnt == g:
z = map(lambda ij: (ij[0] + x, ij[1] + y), points)
if show:
stores.append(list(deepcopy(z)))
aggre = aggre.union(z)
return
p = points[-1]
new = deepcopy(points)
for k in range(len(points) - 2, -1, -1):
i, j = rotate(points[k][0] - p[0], points[k][1] - p[1])
new.append([i + p[0], j + p[1]])
dfs(cnt + 1, new)
aggre = set()
for x, y, d, g in dragons:
dfs(cnt=0, points=start(d))
if show:
for z in stores:
xs, ys = zip(*z)
plt.scatter(xs, ys), plt.plot(xs, ys)
plt.grid(b=True), plt.title('Visualization of Dragons')
plt.show()
ans = 0
for i in range(100):
for j in range(100):
if all(True if (x, y) in aggre else False for x, y in [(i, j), (i + 1, j), (i, j + 1), (i + 1, j + 1)]):
ans += 1
return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
@logging_time
def another(dragons, show=False):
v, ans = [0], 0
a = [[0]*101 for _ in range(101)]
dx, dy = (1, 0, -1, 0), (0, -1, 0, 1)
for i in range(1, 11):
k = 1<<(i-1)
for j in range(k):
v.append((v[k-j-1]+1)%4)
for x, y, d, g in dragons:
a[x][y] = 1
for i in range(1<<g):
x, y = x+dx[(v[i]+d)%4], y+dy[(v[i]+d)%4]
a[x][y] = 1
squares = set()
for i in range(100):
for j in range(100):
if a[i][j] and a[i+1][j] and a[i][j+1] and a[i+1][j+1]:
ans += 1
squares.add((i, j))
if show:
print("squares: ")
print(sorted(squares))
return ans
1
2
3
4
dragons = [(50, 50, 0, 10)]
ans1 = solution(dragons, show=False, verbose=True)
ans2 = another(dragons, show=False, verbose=True)
ans1, ans2
1
2
3
WorkingTime[solution]: 8.72016 ms
WorkingTime[another]: 0.93865 ms
1
(480, 480)
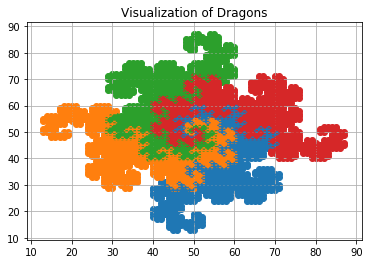
Visualize Dragon Curves
Dragon curve들을 visualize 해보았다.
드래곤 커브의 점matplotlib 의 scatter와 plot을 사용하였다.
points를 set으로 바꾸기 전에 stores 리스트로 저장해놓고, 이를 바탕으로 visualization하였다.
다음은 plot하는 코드이다.
1
2
3
4
5
for z in stores:
xs, ys = zip(*z)
plt.scatter(xs, ys), plt.plot(xs, ys)
plt.grid(b=True), plt.title('Visualization of Dragons')
plt.show()
1
2
3
4
5
6
stdin = open('data/dragon.txt')
input = stdin.readline
n = int(input())
dragons = [list(map(int, input().split())) for _ in range(n)]
print(solution(dragons, show=True, verbose=True))
1
2
3
WorkingTime[solution]: 245.00418 ms
1992
Submitted Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
from sys import stdin
from copy import deepcopy
stdin = open('data/dragon.txt')
input = stdin.readline
n = int(input())
dragons = [list(map(int, input().split())) for _ in range(n)]
def solution(dragons):
rotate = lambda i, j: (-j, i)
def start(dir):
if dir == 0: return [(0, 0), (1, 0)]
if dir == 1: return [(0, 0), (0, -1)]
if dir == 2: return [(0, 0), (-1, 0)]
if dir == 3: return [(0, 0), (0, 1)]
def dfs(cnt, points):
nonlocal aggre, g, x, y
if cnt == g:
aggre = aggre.union(map(lambda ij: (ij[0] + x, ij[1] + y), points))
return
p = points[-1]
new = deepcopy(points)
for k in range(len(points) - 2, -1, -1):
i, j = rotate(points[k][0] - p[0], points[k][1] - p[1])
new.append([i + p[0], j + p[1]])
dfs(cnt + 1, new)
aggre = set()
for x, y, d, g in dragons:
dfs(cnt=0, points=start(d))
ans = 0
for i in range(100):
for j in range(100):
if all(True if (x, y) in aggre else False for x, y in [(i, j), (i + 1, j), (i, j + 1), (i + 1, j + 1)]):
ans += 1
return ans
print(solution(dragons))
1
2
1992
Reference
[1] Beakjoon 문제
[2] Koean rebas’s blog


Leave a comment