399.Evalutate Division

In [12]:

import time, math, sys
from typing import List, Dict
from collections import defaultdict
import networkx as nx
import matplotlib.pyplot as plt
from networkx.drawing.nx_pylab import draw_networkx, draw_networkx_edge_labels, draw_networkx_edges
sys.path.append("/home/swyoo/algorithm/")
from utils.verbose import logging_time, visualize_graph

399. Evaluate Division

DFS

Idea I saw this document[1] to solve this question.
I cited an example as follows.

For example:
Given: a/b = 2.0, b/c = 3.0
We can build a directed graph:
a -- 2.0 --> b -- 3.0 --> c
If we were asked to find a/c, we have:
a/c = a/b * b/c = 2.0 * 3.0
In the graph, it is the product of costs of edges.

Therefore, follow these steps to solve this problem.
Step1. contruct a graph, where the edge weights are reciprocal.
Step2. using the dfs search, aggregate the edges’ rates from source to target.

In [39]:

class Solution:
    @logging_time
    def calcEquation(self, equations: List[List[str]], 
                     values: List[float], queries: List[List[str]],
                    show=False) -> List[float]:
        edges = []  # for visualization
        graph = defaultdict(list)
        nodes = set()
        for (u, v), w in zip(equations, values):
            nodes.add(u), nodes.add(v)
            if show:
                edges.append([v, u, w])
                edges.append([u, v, 1/w])
            graph[v].append((u, w))
            graph[u].append((v, 1/w))
        if show:
            print("edges info:", edges)
            visualize_graph(edges=edges, weighted=True)
        seen = set()
        def dfs(i, target, loc=1):
            seen.add(i)
            if i == target:
                # print("find res:", 1 / loc)
                res.append(1/loc)
                return True
            for j, w in graph[i]:
                if j not in seen and dfs(j, target, loc * w):
                    return True
            return False

        res = []
        for q in queries:
            seen = set()
            if q[0] not in nodes or q[1] not in nodes or not dfs(q[0], q[1]):
                # if fail to find (q[0]/q[1])
                res.append(-1.)
        return res
sol = Solution()

In [40]:

equations = [["a", "b"], ["b", "c"]]
values = [2.0, 3.0]
queries = [["a", "c"], ["b", "a"], ["a", "e"], ["a", "a"], ["x", "x"]]
sol.calcEquation(equations, values, queries, show=True, verbose=True)

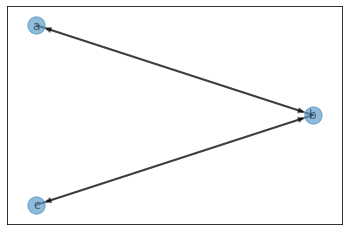
edges info: [['b', 'a', 2.0], ['a', 'b', 0.5], ['c', 'b', 3.0], ['b', 'c', 0.3333333333333333]]

WorkingTime[calcEquation]: 158.74386 ms

[6.0, 0.5, -1.0, 1.0, -1.0]

Improved DFS

I cited a paragraph from this document[1].

One optimization, which is not implemented in the code, is to “compress” paths for past queries, which will make future searches faster. This is the same idea used in compressing paths in union find set. So after a query is conducted and a result is found, we add two edges for this query if these edges are not already in the graph.

Union Find

Union find approach can be possible.
please refer this document

Note that

• Path compression is possible
• However, union by rank does not possible. The algorithm is designed in this way.
  
  1. union(x, y, 0) means find x / y.
  2. w = 0 determines whether to find an answer of a query or not.

In [49]:

from typing import List
from utils.verbose import visualize_ds
class Solution2:
    def calcEquation(self, equations: List[List[str]],
                     values: List[float], queries: List[List[str]],
                     show=False) -> List[float]:
        par = {}
        def find(x):
            if x not in par:
                par[x] = (x, 1)
                return par[x]
            if x != par[x][0]:
                p, pr = find(par[x][0])
                par[x] = (p, par[x][1] * pr)
            return par[x]

        def union(x, y, w):
            """ return x / y.
            if w is 0, query mode, """
            x, xr, y, yr = *find(x), *find(y)
            if not w:
                return xr / yr if x == y else -1.0
            if x != y:
                par[x] = (y, yr/xr*w)

        for (u, v), w in zip(equations, values):
            union(u, v, w)
        ans = []
        for x, y in queries:
            if x not in par or y not in par:
                ans.append(-1.0)
            else:
                ans.append(union(x, y, 0))
        if show:
            print("show disjoint set as follows")
            par = {k: v[0] for k, v in par.items()}
            visualize_ds(par)
        return ans
    
sol2 = Solution2()

In [50]:

equations = [["a", "b"], ["b", "c"]]
values = [2.0, 3.0]
queries = [["a", "c"], ["b", "a"], ["a", "e"], ["a", "a"], ["x", "x"]]
print(sol2.calcEquation(equations, values, queries, show=True))

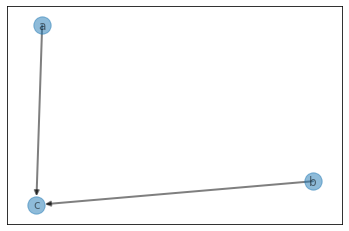
show disjoint set as follows

[6.0, 0.5, -1.0, 1.0, -1.0]

Referenece

[0] leetcode problem
[1] a document in the discuss category of the problem
[2] another document in the discuss category of the problem