1
2
3
4
5
6
7
8
9
import sys, random, string
sys.path.append("/home/swyoo/algorithm/")
from utils.verbose import visualize_graph, logging_time
from utils.generator import randomString
from collections import defaultdict
from pprint import pprint
from copy import deepcopy
from typing import List, Tuple
import numpy as np
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
plot = lambda a: print(np.array(a))
def generate_graph(n, m, randrange:Tuple[int, int] ,verbose=False):
""" |V|: n, |E|: m """
S = set(' '.join(string.ascii_lowercase).split()[:n])
seen = set()
edges = []
for _ in range(m):
while True:
start = randomString(length=1, samples=list(S))
end = randomString(length=1, samples=list(S - {start}))
if (start, end) not in seen:
seen.add((start, end))
break
edges.append((start, end, random.randint(randrange[0], randrange[1])))
if verbose: visualize_graph(edges, weighted=True)
graph = defaultdict(list)
for i in S: graph[i]
for u, v, w in edges:
graph[u].append((v, w))
return graph, edges
# n, m = 10, 5
# graph = generate_graph(n, m, verbose=True)
# graph
Floyd Warshall algorithm
Toy example

1
2
3
4
5
# toy example
graph = {'1':[('2', 3), ('4', 5)],
'2':[('1', 2), ('4', 4)],
'3':[('2', 1)],
'4':[('3', 2)]}
1
2
3
4
5
6
7
8
9
10
11
12
INF = 1e20
def g2m(graph):
n, nodes = len(graph.keys()), sorted(graph.keys())
n2i = {k: v for k, v in zip(nodes, range(n))}
weights = [[INF] * n for _ in range(n)]
for i in nodes: weights[n2i[i]][n2i[i]] = 0
for i in nodes:
for j, w in graph[i]:
weights[n2i[i]][n2i[j]] = w
return n2i, weights
n2i, weights = g2m(graph)
weights
1
2
3
4
[[0, 3, 1e+20, 5],
[2, 0, 1e+20, 4],
[1e+20, 1, 0, 1e+20],
[1e+20, 1e+20, 2, 0]]
Constraints
Floyd Warshall Algorithm is an algorithm for finding shortest paths
in a weighted graph with positive or negative edge weights
(but with no negative cycles)
Naive DP
Idea
$ l_{ij}^{(m)}$: node $i$ 부터 node $j$ 까지 가는데 최대 $m$ 개의 edge를 거쳐서 가는 path의 minimum weight
[intuition]
총 노드의수 를 $n$ 이라하면, 거쳐가는 edge의 수 $m$이 $n-1$보다 많으면 반복되는 node가 존재한다는 뜻이므로 cycle이 있다는 뜻인데,
negative edge가 없다고 가정했으므로 당연히 cycle을 돌면 shortest path의 wieght sum 보다 높은 path sum이 된다.
즉, $m = 1$ 부터 $n - 1$ 까지 update하면 optimal solution이 됨
$ l_{ij}^{(m)} = {min}{(l_{ij}^{(m-1)}, \underset{1 \le k \le n}{min}{(l_{ik}^{(m-1)} + w_{kj} )} )} = \underset{1 \le k \le n}{min}{(l_{ik}^{(m-1)} + w_{kj} )} ~~~~ \text{if } m \ge 1$
$\because k = j $ 이면 $w_{jj}=0$ 이 되므로 case가 합쳐질수 있다.
따라서, recursive formula 는 다음과 같다.
\(l_{ij}^{(m)} =
\begin{cases}
\underset{1 \le k \le n}{min}{(l_{ik}^{(m-1)} + w_{kj})} & \text{if } m \ge 1 \\
l_{ij}^{(0) } =
\begin{cases}
0 & \text{if } i = j\\
\infty & \text{if } i \neq j
\end{cases} & \text{if } m = 0 \\
\end{cases}\)
여기서 또 주목할 만한점은 $m=1 $ 일때는 $l_{ij}^{(1)} = w_{ij}$ 이므로 $l_{ij}^{(0)}$을 굳이 계산할 필요는 없다.
Time Complexity
$O(n^4)$ $ \because n^3$ entries, each entry takes $O(n)$
Pseudo Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# update next step for m
update(L,W)
n = len(L)
let L`[1..n, 1..n] be a new array
for i = 1 to n
for j = 1 to n
L`[i,j] = INF
# each entry can be calculated in O(n)
for k = 1 to n
L`[i,j] = min(L`[i.j], L[i.j] + W[k,j])
return L`
# given a graph's weight matrix W[1..n, 1..n]
Naive(W)
n = len(W)
let L[1..n, 1..n] be a new array
# initialization
L = W
# update L for m
for m = 2 to n-1
L = update(L, W)
retrun L
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
@logging_time
def naive(weights):
n = len(weights)
def update(a):
b = [[INF] * n for _ in range(n)]
for i in range(n):
for j in range(n):
for k in range(n):
b[i][j] = min(b[i][j], a[i][k] + weights[k][j])
return b
ans = weights # initial states
for m in range(2, n):
ans = update(ans)
return ans
plot(naive(weights, verbose=True))
1
2
3
4
5
6
WorkingTime[naive]: 0.05555 ms
[[0 3 7 5]
[2 0 6 4]
[3 1 0 5]
[5 3 2 0]]
Improved Naive
$m$ 에 대해 linear 하게 update 하는 위의 방식을 조금 더 개선해보자.
L 의 계산이 associative(결합법칙을 만족)한 성질을 가지며, $m \ge n - 1$이면 shortest path weight는 고정되어 $L$ 은 바뀌지 않는다.
따라서, associative 하게 $k$번 계산하여 $2^k \ge n-1$ 일 경우 optimal sol으로 고정된다.
따라서, optimal sol에 도달하기 까지 $k = O(logn)$ 번 연산하게 됨.
\(\begin{aligned}
L^{(1)} &= W \\
L^{(2)} &= W^2 = WW \\
L^{(4)} &= W^4 = W^2W^2\\
... \\
L^{(2^k)} &= W^{2^k} = W^kW^k\\
L^{(2^k \ge~ n-1)} &= W^{2^k \ge ~ n-1} (fixed)\\
\end{aligned}\)
Pseudo Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# given a graph's weight matrix W[1..n, 1..n]
faster_APSP(W)
n = len(W)
let L[1..n, 1..n] be a new array
# initialization
L = W
# update L for m
m = 2
while m < n-1
L = update(L, L)
m = m*2
retrun L
$O(n^3logn)$ 으로 계선되었지만 여전히 비싼 알고리즘이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
@logging_time
def improved(weights):
n = len(weights)
def update(a):
b = [[INF] * n for _ in range(n)]
for i in range(n):
for j in range(n):
for k in range(n):
b[i][j] = min(b[i][j], a[i][k] + a[k][j])
return b
ans = weights # initial states
m = 1
while m < n:
ans = update(ans)
m *= 2
return ans
plot(improved(weights, verbose=True))
1
2
3
4
5
6
WorkingTime[improved]: 0.05364 ms
[[0 3 7 5]
[2 0 6 4]
[3 1 0 5]
[5 3 2 0]]
Idea of Floyd Warshall Algorithm
All pair shortest path with DP 를 조금더 효율적으로 해보자는 접근
기본 가정: no negative cycle
먼저 주어진 그래프에 대한 edge정보로 부터 matrix $C$ 정의
\(C_{ij} = \left \{
\begin{matrix}
0 & \text{if } i=j \\
c(i,j) \ge 0 & \text{if } i \ne j, (i,j) \in E \\
\infty & \text{if } i \ne j, (i,j) \notin E \\
\end{matrix}\right.\)
$d_{ij}^{(k)}$: $v_i \text{~} v_j$ 까지 가는데 $v_1, .., v_k$를 거쳐가는지에 대한 유무가 update된 shortest path distance
($k$ 가 증가함에따라 점점 더 많은 노드정보를 거쳐가는것에 대한 정보를 업데이트 된다).
 \(d_{ij}^{(k)} = \left \{
\begin{matrix}
c(i,j) \ge 0 & \text{if } k=0 \\
min \{ d_{ij}^{(k-1)}, d_{ik}^{(k-1)} + d_{kj}^{(k-1)} \} & \text{if } k \ge 1 \\
\end{matrix} \right.\)
\(d_{ij}^{(k)} = \left \{
\begin{matrix}
c(i,j) \ge 0 & \text{if } k=0 \\
min \{ d_{ij}^{(k-1)}, d_{ik}^{(k-1)} + d_{kj}^{(k-1)} \} & \text{if } k \ge 1 \\
\end{matrix} \right.\)
Time Complexity
$O(n^3)$ because all entry $(1\le i,j,k\le n)$ , is $n^3$, each entry takes $O(n)$ time
Back Propagation: $P^{(k)}$의 각 entry $P_{ij}^{(k)}$가 의미하는것은 현재까지 업데이트된 $v_k$ 를 지나는 $v_i \rightsquigarrow v_k \rightsquigarrow v_j$ 의 shortest path 정보를 의미한다.
($k = 1,..,n$ 까지 모두 update되어야 진짜 shortest path가 됨)

Implementation
1
2
3
4
5
6
7
8
9
10
11
@logging_time
def floyd(weights):
n = len(weights)
ans = deepcopy(weights)
for k in range(n):
for i in range(n):
for j in range(n):
ans[i][j] = min(ans[i][j], ans[i][k] + ans[k][j])
return ans
plot(floyd(weights, verbose=True))
1
2
3
4
5
6
WorkingTime[floyd]: 0.05054 ms
[[0 3 7 5]
[2 0 6 4]
[3 1 0 5]
[5 3 2 0]]
Application
Detect Negative Cycles
Floyd Warshall Algorithm based solution is discussed that works for both connected and disconnected graphs.
connected의 유무와 상관없이 negative cycle들을 detect할 수 있다!
wiki의 Behavior with negative cycles part 에도 설명이 나와있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def hasNcycles(weights, verbose=False):
n = len(weights)
ans = deepcopy(weights)
for k in range(n):
for i in range(n):
for j in range(n):
ans[i][j] = min(ans[i][j], ans[i][k] + ans[k][j])
# check if negative cycle exist
for i in range(n):
if ans[i][i] < 0:
if verbose: print("negative cycle exists from node[{}] to node[{}]".format(i, i))
return True
return False
hasNcycles(weights)
1
False
Analysis
For small dataset
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def generate_graph_no_neg_cycle(n, m, verbose=False):
weights = graph = None
while True:
graph, edges = generate_graph(n, m, randrange=(-5, 10), verbose=verbose)
n2i, W = g2m(graph)
if not hasNcycles(W):
weights = deepcopy(W)
return n2i, weights, graph, edges
n, m = 5, 10
n2i, weights, graph, edges = generate_graph_no_neg_cycle(n, m, verbose=False)
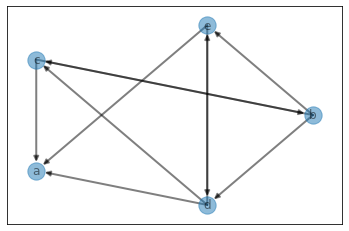
visualize_graph(edges=edges, weighted=True)
pprint(graph)
pprint(n2i)
plot(weights)
ans1 = naive(weights, verbose=True)
ans2 = improved(weights, verbose=True)
ans3 = floyd(weights, verbose=True)
# plot(ans1), plot(ans2), plot(ans3)
assert ans1 == ans2 == ans3
plot(ans1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
defaultdict(<class 'list'>,
{'a': [],
'b': [('e', -3), ('d', 9), ('c', -1)],
'c': [('b', 6), ('a', 1)],
'd': [('e', 7), ('a', 8), ('c', -2)],
'e': [('a', 6), ('d', 6)]})
{'a': 0, 'b': 1, 'c': 2, 'd': 3, 'e': 4}
[[ 0.e+00 1.e+20 1.e+20 1.e+20 1.e+20]
[ 1.e+20 0.e+00 -1.e+00 9.e+00 -3.e+00]
[ 1.e+00 6.e+00 0.e+00 1.e+20 1.e+20]
[ 8.e+00 1.e+20 -2.e+00 0.e+00 7.e+00]
[ 6.e+00 1.e+20 1.e+20 6.e+00 0.e+00]]
WorkingTime[naive]: 0.14782 ms
WorkingTime[improved]: 0.13828 ms
WorkingTime[floyd]: 0.06795 ms
[[ 0.e+00 1.e+20 1.e+20 1.e+20 1.e+20]
[ 0.e+00 0.e+00 -1.e+00 3.e+00 -3.e+00]
[ 1.e+00 6.e+00 0.e+00 9.e+00 3.e+00]
[-1.e+00 4.e+00 -2.e+00 0.e+00 1.e+00]
[ 5.e+00 1.e+01 4.e+00 6.e+00 0.e+00]]
For large dataset
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
def generate_graph(n, m, randrange:Tuple[int, int], verbose=False):
""" |V|: n, |E|: m """
# S = set(' '.join(string.ascii_lowercase).split()[:n])
S = set(range(n))
seen = set()
edges = []
for _ in range(m):
while True:
# start = randomString(length=1, samples=list(S))
# end = randomString(length=1, samples=list(S - {start}))
start, end = random.choices(population=range(n - 1), k=2)
if (start, end) not in seen:
seen.add((start, end))
break
edges.append((start, end, random.randint(randrange[0], randrange[1])))
if verbose: visualize_graph(edges, weighted=True)
graph = defaultdict(list)
for i in S: graph[i]
for u, v, w in edges:
graph[u].append((v, w))
return graph, edges
def generate_graph_no_neg_cycle(n, m, randrange):
weights = graph = None
while True:
graph, edges = generate_graph(n, m, randrange, verbose=False)
n2i, W = g2m(graph)
if not hasNcycles(W):
weights = deepcopy(W)
return n2i, weights, graph, edges
n, m = 50, 300
n2i, weights, graph, edges = generate_graph_no_neg_cycle(n, m, randrange=(-10, 100))
print("A graph is generated!")
visualize_graph(edges=edges, weighted=True)
ans1 = naive(weights, verbose=True)
ans2 = improved(weights, verbose=True)
ans3 = floyd(weights, verbose=True)
# plot(ans1), plot(ans2), plot(ans3)
# assert ans1 == ans2 == ans3
plot(ans3)
1
2
A graph is generated!

1
2
3
4
5
6
7
8
9
10
11
WorkingTime[naive]: 1775.65432 ms
WorkingTime[improved]: 208.99677 ms
WorkingTime[floyd]: 37.94217 ms
[[0.0e+00 3.8e+01 4.0e+01 ... 5.6e+01 1.9e+01 1.0e+20]
[4.0e+00 0.0e+00 2.8e+01 ... 4.9e+01 2.3e+01 1.0e+20]
[4.5e+01 6.2e+01 0.0e+00 ... 8.2e+01 5.7e+01 1.0e+20]
...
[1.9e+01 2.3e+01 5.0e+01 ... 0.0e+00 3.8e+01 1.0e+20]
[5.0e+00 2.5e+01 2.9e+01 ... 4.5e+01 0.0e+00 1.0e+20]
[1.0e+20 1.0e+20 1.0e+20 ... 1.0e+20 1.0e+20 0.0e+00]]
Reference
[1] geeksforgeeks - visualization of a graph
[2] referenced blog - floyd warshall algorithm
[3] geeksforgeeks - detect negative cycles
[4] c++ implementation


Leave a comment