785.Is Graph Bipartite

In [28]:

import sys
sys.path.append("/home/swyoo/algorithm/")
from utils.verbose import visualize_graph
from typing import List
from collections import defaultdict, deque

785. Is Graph Bipartite?

Idea

If a graph is bipartite, two coloring is possible!
If conflict is occured while coloring process, isBipartite flag become False.
I saw this idea from this document

DFS

In [30]:

class Solution1:
    def isBipartite(self, graph: List[List[int]]) -> bool:
        color = {}  # True: red, False: black
        isbipartite = True
        def dfs(i, paint):
            nonlocal isbipartite
            color[i] = paint
            for j in graph[i]:
                if j not in color:
                    dfs(j, paint=~color[i])
                elif color[i] == color[j]:
                    isbipartite = False
        for x in range(len(graph)):
            if x not in color:
                dfs(x, paint=False)
        return isbipartite
    
sol1 = Solution1()    

In [31]:

# toy example
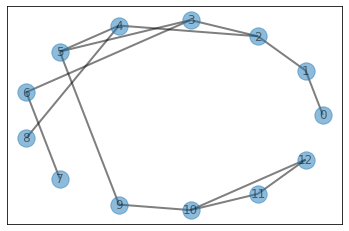
edges = [[0,1],[1,2],[2,3],[2,4],[3,5],[4,5],[3,6],[4,8],[6,7],[5,9],[9,10],[10,11],[11,12],[10,12]]
graph = defaultdict(list)
for u,v in edges:
    graph[u].append(v)
visualize_graph(edges, undirected=True)

In [32]:

sol.isBipartite(graph)

False

In [33]:

class Solution2:
    def isBipartite(self, graph: List[List[int]]) -> bool:
        color = {}  # True: red, False: black
        isBipartite = True
        def bfs(s):
            nonlocal isBipartite
            color[s] = False
            queue = deque([(s, color[s])])
            while queue:
                i, paint = queue.popleft()
                for j in graph[i]:
                    if j not in color:
                        color[j] = ~paint
                        queue.append((j, color[j]))
                    elif paint == color[j]:
                        isBipartite = False
        for x in range(len(graph)):
            if x not in color:
                bfs(x)
        return isBipartite
sol2 = Solution2()    

In [34]:

sol2.isBipartite(graph)

False

Reference

[1] a detailed document
[2] leetcode problem