14.LCP using python - Leetcode

Suppose that $n$ be len(strs), $M$ be a maxium string of strs.
There are three ways to solve this problem.

1. Linear Search: $O(nM)$
2. Divide and Conquer: $O(nM)$ GeeksforGeeks
   
3. Binary Search: $O(nMlogM)$ GeeksforGeeks

In [1]:

# toy examples
M = 6 # len of longest string
strs1 = ["flowers", "flow", "flights"]
strs2 = ["dog", "racecar", "car"]

Linear Search

find LCP = str[0][:i], seaching through str[j] linearly.

In [2]:

def LCP_linear(strs):
    # base cases
    if len(strs) == 0: 
        return ""
    if len(strs) == 1:
        return strs[0]
    
    # linear scan to find Longest Common Prefix 
    # initialization
    tmp = strs[0]
    for j in range(1, len(strs)):
        # finish is the length of possible maximum LCP
        # tmp be possible maximum LCP 
        finish = min(len(tmp), len(strs[j]))
        tmp = strs[0][:finish]
        # search to find LCP precisely
        for i in range(finish):
            if tmp[i] != strs[j][i]:
                tmp = strs[0][:i]
                break
    return tmp

In [3]:

print("ex1: ", LCP_linear(strs1))
print("ex2: ", LCP_linear(strs2))

ex1:  fl
ex2:  

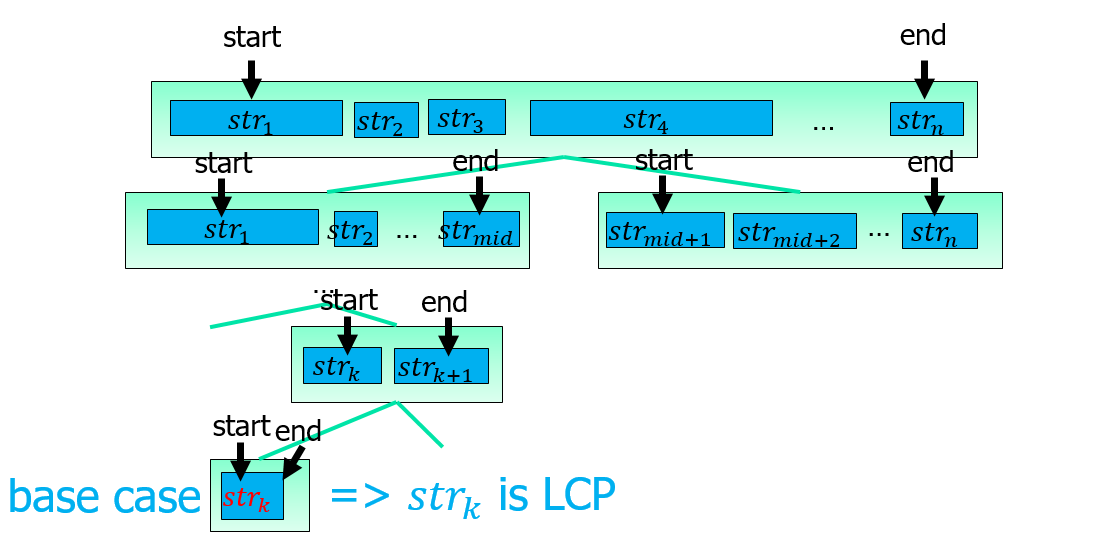
Divide and Conquer

• find left part and right part of LCP.
• find LCP between left part and right part.

key idea is described as follows.

Time complexity analysis

\(\begin{align} T(n) &= 2T(n/2) + M \\ &= 2(2T(n/2^2) + M) + M \\ &= 2^k(T(n/2^k) + (1 + 2 + ... + 2^{k-1})M \\ &= 2^k(T(n/2^k) + (2^{k} - 1)M \\ &= n(T(1) + (n - 1)M \\ &= O(nM) \\ \end{align}\)

In [4]:

# O(M)
def Util(s1, s2):
    """ find LCP between s1 and s2. """
    finish = min(len(s1), len(s2))
    tmp = s1[:finish]
    for i in range(finish):
        if s1[i] != s2[i]:
            tmp = s1[:i]
            break
    return tmp

def LCP(strs, p, r):
    if len(strs) == 0:
        return ""
    if p >= r:
        return strs[p]
    mid = (p + r)//2
    s1 = LCP(strs, p, mid)
    s2 = LCP(strs, mid + 1, r)
    return Util(s1, s2)

In [5]:

print("ex1: ", LCP(strs1, 0, len(strs1)-1))
print("ex2: ", LCP(strs2, 0, len(strs2)-1))

ex1:  fl
ex2:  

Binary Search

1. select the smallest word (to void index overflow, which has length $M$), let it be loc, in example, geek
2. let mid = (s + e)//2, where s, e are start, last index for each.
3. call(s, mid) and in there, check all words to match them with loc[s..mid] to find LCP.
   • if check returns True, append loc[s..e] to ans, and call(mid + 1, e). go to second step.
   • else, call call(s, mid - 1) in order to reset ans. go to second step.

In this way, we call only left-half or right-helf recursion by checking process, which is a binary search technique.
Note that checking process takes $O(nM)$.
Recursive formula as follows.
\(T(M) = T(M/2) + O(nM) = O(nMlogM)\)

In [6]:

def solve(strs):
    def check(base, s, e):
        """ """
        for i in range(len(strs)):
            j = s
            while j <= e and base[j] == strs[i][j]: j += 1
            if j != e + 1: return False
        return True

    def findLCP(loc, s, e):
        if s > e: return ""
        if s == e:
            return loc[s] if check(loc, s, e) else ""
        mid = (s + e) // 2
        if check(loc, s, mid):
            return loc[s:mid+1] + findLCP(loc, mid+1, e)
        else:
            return findLCP(loc, s, mid-1)

    m = len(strs[0]) # length of the shortest word.
    loc = strs[0]
    for _ in range(len(strs)):
        if m > len(strs[_]):
            m = len(strs[_])
            loc = strs[_]
    return findLCP(loc, 0, m - 1)

In [7]:

strs = ["geeksforgeeks", "geeks", "geek", "geezer"]
solve(strs)

'gee'

However, it is too slow, and overhead makes time limited when submitted.
Therefore, iterative solution as follows to avoid overhead(it can be passed in leetcode).

In [8]:

class Solution(object):

    def findMinLength(self, strList):
        m = len(strList[0])
        for st in strList:
            m = min(m, len(st))
        return m

    def allContainsPrefix(self, strList, str, start, end):
        for i in range(0, len(strList)):
            word = strList[i]
            for j in range(start, end + 1):
                if word[j] != str[j]:
                    return False
        return True

    def longestCommonPrefix(self, strList):
        if len(strList) == 0: return ""
        index = self.findMinLength(strList)
        prefix = ""  # Our resultant string
        # We will do an in-place binary search
        # on the first string of the array
        # in the range 0 to index
        low, high = 0, index - 1
        while low <= high:
            # Same as (low + high)/2, but avoids
            # overflow for large low and high
            mid = int(low + (high - low) / 2)
            if self.allContainsPrefix(strList, strList[0], low, mid):
                # If all the strings in the input array
                # contains this prefix then append this
                # substring to our answer
                prefix = prefix + strList[0][low:mid + 1]
                # And then go for the right part
                low = mid + 1
            else:
                # Go for the left part
                high = mid - 1
        return prefix 
sol = Solution()

In [9]:

strs = ["geeksforgeeks", "geeks", "geek", "geezer"]
sol.longestCommonPrefix(strList=strs)

'gee'