In [1]:
1
2
3
4
from typing import List
import sys, random
sys.path.append("/home/swyoo/algorithm/")
from utils.verbose import logging_time, visualize_ds
128. Longest Consecutive Sequence
Disjoint Set(or Union Find)
With Sorting
\(O(nlogn)\)
In [2]:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Disjoint Set data structure
par, rnk = {}, {}
cnt = {}
def find(x):
if x not in par:
par[x] = x
rnk[x] = 0
cnt[x] = 1
return par[x]
if x != par[x]:
par[x] = find(par[x])
return par[x]
def union(x, y):
x, y = find(x), find(y)
if x == y: return
if rnk[x] > rnk[y]:
x, y = y, x
par[x] = y
cnt[y] += cnt[x]
if rnk[x] == rnk[y]:
rnk[y] += 1
In [3]:
1
2
3
4
5
6
7
8
9
10
11
12
class Solution1:
@logging_time
def longestConsecutive(self, nums: List[int], show=False) -> int:
if not nums: return 0
nums = sorted(nums)
for i in range(1, len(nums)):
if nums[i] - nums[i - 1] == 1:
union(nums[i - 1], nums[i])
if show: visualize_ds(par)
return max(cnt.values()) if cnt else 1
sol1 = Solution1()
In [4]:
1
2
A = [100,4,200,1,3,2]
print(sol1.longestConsecutive(A, show=True, verbose=True))
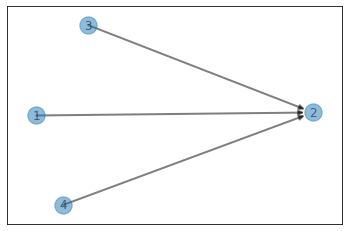
1
2
3
WorkingTime[longestConsecutive]: 173.99216 ms
4
Without Sorting
If the algorithm use some techniques as follows, it can be improved.
- Conversion of
numsfrom list to set: checking if exist takes $O(1)$. - Both ‘path compression’ ans ‘union by rank’
The time complexity of the whole process becomes as follows.
\(O(n\alpha)\)
In [5]:
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution2:
@logging_time
def longestConsecutive(self, nums: List[int], show=False) -> int:
if not nums: return 0
nums = set(nums)
used = set()
for e in nums:
if e not in used and e - 1 in nums:
union(e - 1, e)
used.add(e)
if show: visualize_ds(par)
return max(cnt.values()) if cnt else 1
sol2 = Solution2()
In [6]:
1
2
par, rnk, cnt = {}, {}, {}
print(sol2.longestConsecutive(A, show=True, verbose=True))
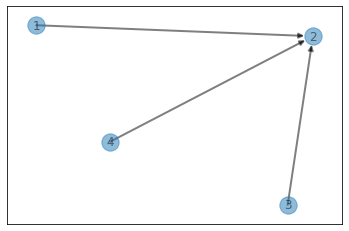
1
2
3
WorkingTime[longestConsecutive]: 162.27818 ms
4
In [7]:
1
2
size = 10000000
A = [random.randint(-size*10, size*10) for i in range(size)]
In [8]:
1
2
3
4
par, rnk, cnt = {}, {}, {}
ans1 = sol1.longestConsecutive(A, verbose=True)
par, rnk, cnt = {}, {}, {}
ans2 = sol2.longestConsecutive(A, verbose=True)
1
2
3
WorkingTime[longestConsecutive]: 6538.45930 ms
WorkingTime[longestConsecutive]: 3892.41171 ms
Without Disjoint Set
I imported a solution from a document of the discuss
In [9]:
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution3:
@logging_time
def longestConsecutive(self, nums):
nums = set(nums)
best = 0
for x in nums:
if x - 1 not in nums:
y = x + 1
while y in nums:
y += 1
best = max(best, y - x)
return best
sol3 = Solution3()
In [10]:
1
ans3 = sol3.longestConsecutive(A, verbose=True)
1
2
WorkingTime[longestConsecutive]: 4654.11186 ms
In [11]:
1
ans1, ans2, ans3
1
(6, 6, 6)


Leave a comment