851.Loud and Rich using python - Leetcode

In [1]:

import sys
sys.path.append("/home/swyoo/algorithm")
from utils.verbose import logging_time, printProgressBar
from collections import defaultdict

851. Loud and Rich

Objective

For each person,

• Find people who has same, or more money (including myself).
• Answer the index of a person who has the least quiet value among people who have same, or more money.

즉, 각 person마다 돈을 같거나 더 많이 가진 사람 중에서(자신 포함) 가장 quiet 값이 작은 사람의 index를 ans 에 output하면 된다.

leetcode
good code
YouTube

Key Idea

Make Graph(adjacent list)

각 사람마다 돈을 더 많이 가진 사람들에 대한 정보를 dictionary money 로 저장해놓는다. (adjacent list 형식이 된다.)

# set graph, reflect money information(hash people same or more money).
n = len(quiet)
money = defaultdict(list)
for i, j in richer:
    money[j].append(i)  # store people who have more money than person i

Use DFS

dictionary money 를 바탕으로 dfs 를 통해 explore 하면서 가장 quiet 값이 작은 사람을 발견했다면, ans 를 업데이트 한다.

• dfs(i) 의 return 값은 돈이 같거나 더 많은 사람들 중에 quiet값이 가장 작은 사람의 index이다.

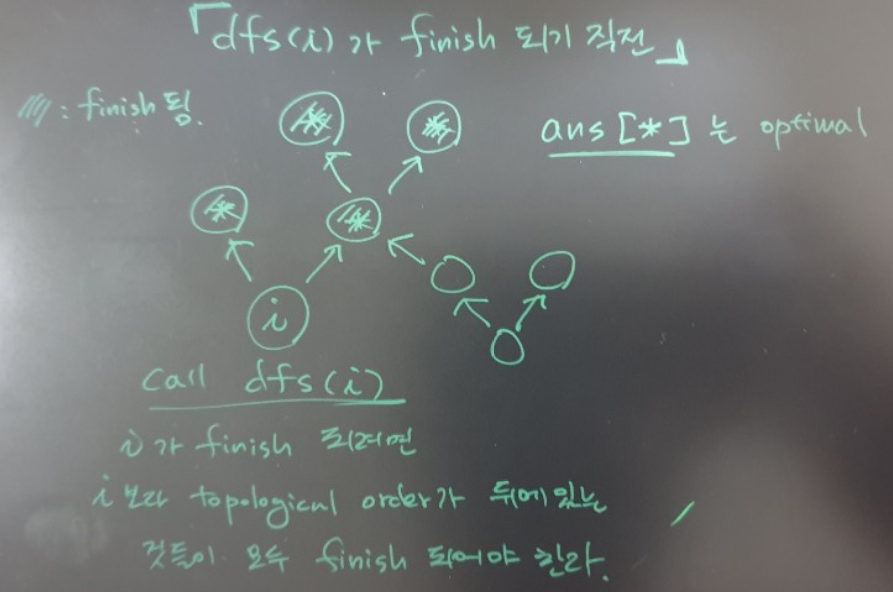
  dictionary money를 바탕으로 exploration하면서 ans가 업데이트 되고, 가능한 모든 case 를 exploration하면 finish 되는데
  finish 되었다는 것은 graph 에서 topolgical order에 들어있는
  모든 people index에 해당하는 ans[*]들이 finish 되어야 ans[i] 도 finish 된다. [밑의 그림 참조]
  
  중요한 점은 적어도 최소한 ans[i]는 원하는 값(optimal value)이 최종적으로 update되어서 앞으로 변하지 않을 것이라는 것을 보장한다.
  따라서, 모든 i = 0, ... n-1 에 대해 dfs(i)함수를 call하면 모든 ans[i]에 optimal value가 결정된다.
  

    for i in range(n):
        dfs(i)
  

Use caching

이전에 dfs(i) 를 call한 적이 있다면 ans[*]들은 optimal 값을 가진다.
따라서, 또 recursion할 필요없이 cache된 값들을 그대로 쓰자. (*는 i보다 topological order가 뒤에 있는 index들)
이때, ans[*]들은 한번이상 call되었으며 fixed된 값이며 -1 보다 큰 값이다.

if ans[i] >= 0: # if ans is cached, use it.
    return ans[i]

따라서, caching을 통한 DFS를 하면 모든 person index 에 대해 한번씩만 finish 하게 되므로 Time complexity 는 다음과 같다. \(O(n)\)

In [2]:

@logging_time
def solve(richer, quiet):
    def dfs(i):
        """ update possible answers related to person i by seeing money information.
        that is, determine a person who has the least quiet value related to person i
        Therefore, after calling dfs(i),
        ans[i] is determined certainly at the finishing time, so returns it. """
        if ans[i] >= 0: # if ans is cached, use it.
            return ans[i]
        ans[i] = i # update information by itself(same money)
        # update information by people who have more money than person i
        for j in money[i]:
            # take a person who have the least quiet value.
            if quiet[ans[i]] > quiet[dfs(j)]:
                ans[i] = ans[j] # by calling dfs(j), ans[j] is determined certainly.
        return ans[i] # ans[i] is determined certainly(fixed)

    # set graph, reflect money information(hash people same or more money).
    n = len(quiet)
    money = defaultdict(list)
    for i, j in richer:
        money[j].append(i)  # store people who have more money than person i
    ans = [-1] * n
    for i in range(n):
        dfs(i)
    return ans

In [3]:

richer = [[1, 0], [2, 1], [3, 1], [3, 7], [4, 3], [5, 3], [6, 3]]
quiet = [3, 2, 5, 4, 6, 1, 7, 0]
print(solve(richer, quiet, verbose=True))

WorkingTime[solve]: 0.01478 ms
[5, 5, 2, 5, 4, 5, 6, 7]

Experiment

caching이 없을 경우엔 이미 방문한 ans[k] 에 대한 optimal 값을 또 다시 찾기 위해
money를 보며 k보다 topological order가 뒤에 오는 index들에 대해 모두 recursion 한다.
따라서, redundancy가 생겨 시간이 느려진다.
time complexity는 각 dfs 마다 $O(n)$ 시간이 걸리므로, 모든 index 마다 dfs를 call하면 다음과 같다. \(O(n^2)\)

In [4]:

@logging_time
def solve(richer, quiet):
    def dfs(i):
        """ update possible answers related to person i by seeing money information.
        that is, determine a person who has the least quiet value related to person i
        Therefore, after calling dfs(i),
        ans[i] is determined certainly at the finishing time, so returns it. """
        # if ans[i] >= 0: # if ans is cached, use it.
        #    return ans[i]
        ans[i] = i # update information by itself(same money)
        # update information by people who have more money than person i
        for j in money[i]:
            # take a person who have the least quiet value.
            if quiet[ans[i]] > quiet[dfs(j)]:
                ans[i] = ans[j] # by calling dfs(j), ans[j] is determined certainly.
        return ans[i] # ans[i] is determined certainly(fixed)

    # set graph, reflect money information(hash people same or more money).
    n = len(quiet)
    money = defaultdict(list)
    for i, j in richer:
        money[j].append(i)  # store people who have more money than person i
    ans = [-1] * n
    for i in range(n):
        dfs(i)
    return ans

In [5]:

print(solve(richer, quiet, verbose=True))

WorkingTime[solve]: 0.06175 ms
[5, 5, 2, 5, 4, 5, 6, 7]

Report

이 문제의 핵심은 richer로 부터 그래프 형식을 만들고, dfs를 사용하며 quiet 정보를 바탕으로 ans를 update하는 문제였다.
상당히 깔끔하게 풀릴 수 있어, 좋은 문제인 것 같다.

ETC

이 문제는 주어진 문제의 input richer 에서 x가 y보다 richer고, y 가 x보다 richer인 모순적인 상황은 없다.
이 말은 즉슨, richer로 graph정보를 나타내도록 dictionary를 만들 경우, cycle이 생기지 않는다는 뜻이고, dfs를 call 할 경우 굳이 visited 정보를 저장할 필요는 없다.