1
2
3
4
5
6
7
8
9
10
from typing import List, Dict
from collections import defaultdict
import networkx as nx
import matplotlib.pyplot as plt
from networkx.drawing.nx_pylab import draw_networkx
from pprint import pprint
import numpy as np
import sys
sys.path.append("/home/swyoo/algorithm/")
from utils.verbose import logging_time
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def visualize(par):
""" visualize disjoint set data structure.
:param: par: dictionary, which contains hierachical information of the disjoint set. """
adj = defaultdict(list)
edges = []
for k, v in par.items():
adj[k].append(v)
edges.append((k, v))
g = nx.DiGraph()
g.add_edges_from(edges)
# pos = nx.circular_layout(g)
pos = nx.spring_layout(g, k=0.5, scale=10)
draw_networkx(g, pos=pos, with_labels=True, width=2.0, alpha=0.5)
plt.show()
947. Most Stones Removed with Same Row or Column
Remove all possible stones aligned with same row and column, and count how many stones are removed.
Constraints are as follows.
1
2
1 <= stones.length <= 1000
0 <= stones[i][j] < 10000
Let stones.length be $n$, the max index of stones be $m$
1
2
3
4
5
6
7
# toy example
stones = [[0,0],[0,1],[1,0],[1,2],[2,1],[2,2]]
m = max(max(stone)for stone in stones) + 1
grid = np.zeros(shape=(m, m), dtype=int)
for stone in stones:
grid[stone[0], stone[1]] = 1
grid
1
2
3
array([[1, 1, 0],
[1, 0, 1],
[0, 1, 1]])
1
2
3
4
5
6
7
8
# m, rate = 10000, 0.00001
# # m, rate = 5, 0.2
# grid = np.random.choice(a=[0, 1], size=(m, m), p=[1 - rate, rate])
# if m < 10: print('grid: \n', grid)
# stones = [[i, j] for i, rows in enumerate(grid) for j, e in enumerate(rows) if e]
# if m < 10: print('stones:', stones)
# n = len(stones)
# n
Naive
Enumerate all cases
see all indices by removing stones for each stone.
It takes $O(n^m)$.
DFS
Idea
I use this idea in leetcode discuss.
This is efficient implementation.
It takes $O(n)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution1:
@logging_time
def removeStones(self, stones: List[List[int]]) -> int:
rows, cols = defaultdict(list), defaultdict(list)
for i, j in stones:
rows[i].append(j)
cols[j].append(i)
seen = set()
def dfs(i, j):
seen.add((i, j))
for jj in rows[i]:
if (i, jj) not in seen:
dfs(i, jj)
for ii in cols[j]:
if (ii, j) not in seen:
dfs(ii, j)
cnt = 0 # count the number of representatives.
for i, j in stones:
if (i, j) not in seen:
cnt += 1
dfs(i, j)
return len(stones) - cnt
sol1 = Solution1()
1
ans1 = sol1.removeStones(stones, verbose=True)
1
2
WorkingTime[removeStones]: 0.01550 ms
Union Find
Approach 1
1
2
3
4
cnt = 0
for s in stones:
if str(s) == find(str(s)):
cnt += 1
which is implemented in one line as follows.
1
len(stones) - len({find(str(s)) for s in stones})
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution2:
@logging_time
def removeStones(self, stones: List[List[int]], show=False) -> int:
par, rnk = {}, {}
def find(x):
if x not in par:
par[x] = x
rnk[x] = 0
return x
if x != par[x]:
par[x] = find(par[x])
return par[x]
def union(x, y):
x, y = find(x), find(y)
if x == y: return
if rnk[x] > rnk[x]:
x, y = y, x
par[x] = y
if rnk[x] == rnk[y]:
rnk[y] += 1
for i in range(len(stones)):
for j in range(i, len(stones)):
s1, s2 = stones[i], stones[j]
if s1[0] == s2[0] or s1[1] == s2[1]:
union(str(s1), str(s2))
if show:
visualize(par)
return len(stones) - len({find(str(s)) for s in stones})
sol2 = Solution2()
1
print(sol2.removeStones(stones, verbose=True, show=True))
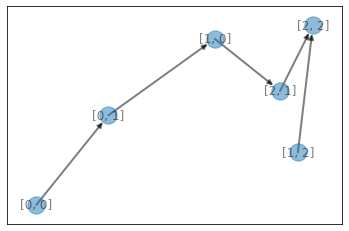
1
2
3
WorkingTime[removeStones]: 206.74706 ms
5
1
grid
1
2
3
array([[1, 1, 0],
[1, 0, 1],
[0, 1, 1]])
1
2
3
4
5
6
7
8
9
10
11
12
m, rate = 10000, 0.00001
# m, rate = 5, 0.2
grid = np.random.choice(a=[0, 1], size=(m, m), p=[1 - rate, rate])
if m < 10: print('grid: \n', grid)
stones = [[i, j] for i, rows in enumerate(grid) for j, e in enumerate(rows) if e]
n = len(stones)
print("# of stones:", n)
if m < 10: print('stones:', stones)
ans1 = sol1.removeStones(stones, verbose=True)
ans2 = sol2.removeStones(stones, verbose=True, show=False)
print("ans:", ans1)
assert ans1 == ans2
1
2
3
4
5
# of stones: 980
WorkingTime[removeStones]: 1.22046 ms
WorkingTime[removeStones]: 76.24412 ms
ans: 89
Approach 2: Improved
You must union for stones in the same row or column. We can union this wisely in $O(n\alpha)$.
we can incrementally union stones by differentiating row and column indices. I refered this article.
1
2
3
for i, j in stones:
union(i, ~j)
return len(stones) - len({find(x) for x, y in stones})
or
1
2
3
for i, j in stones:
union(~i, j)
return len(stones) - len({find(y) for x, y in stones})
How can be possible?
Let’s look at two episodes.
First episode tells us that stones with same rows can be unioned incrementally.
(Please note that a stone can be represented by ((i)->(~j)) like a dipole structure. :).)
..., [i, j1], [i, j2], ...
union(i, ~j1), and then, union(i, ~j2), where i can be repeated, so [i, j1] and [i, j2] are unioned.
This Second episode tells us that stones with same cols can be unioned incrementally.
..., [i1, j], [i2, j], ...
union(i1, ~j), and then, union(i2, ~j), where j can be repeated, so [i1, j] and [i2, j] are unioned.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution3:
@logging_time
def removeStones(self, stones: List[List[int]], show=False) -> int:
par, rnk = {}, {}
def find(x):
if x not in par:
par[x] = x
rnk[x] = 0
return x
if x != par[x]:
par[x] = find(par[x])
return par[x]
def union(x, y):
x, y = find(x), find(y)
if x == y: return
if rnk[x] > rnk[x]:
x, y = y, x
par[x] = y
if rnk[x] == rnk[y]:
rnk[y] += 1
for i, j in stones:
union(i, ~j)
if show:
visualize(par)
return len(stones) - len({find(x) for x, y in stones})
# return len(stones) - len({find(y) for x, y in stones})
sol3 = Solution3()
1
sol3.removeStones(stones, verbose=True, show=False)
1
2
WorkingTime[removeStones]: 1.19972 ms
1
89
1
2
3
4
5
6
7
# toy example
stones = [[0,0],[0,1],[1,0],[1,2],[2,1],[2,2]]
m = max(max(stone)for stone in stones) + 1
grid = np.zeros(shape=(m, m), dtype=int)
for stone in stones:
grid[stone[0], stone[1]] = 1
grid
1
2
3
array([[1, 1, 0],
[1, 0, 1],
[0, 1, 1]])
1
2
print(sol2.removeStones(stones, verbose=True, show=True))
print(sol3.removeStones(stones, verbose=True, show=True))
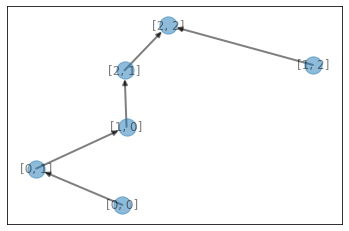
1
2
3
WorkingTime[removeStones]: 194.06533 ms
5
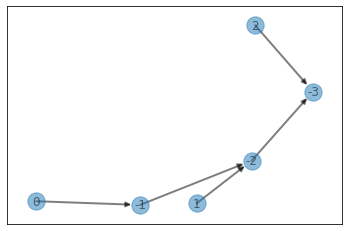
1
2
3
WorkingTime[removeStones]: 194.32855 ms
5


Leave a comment