Karatsuba Algorithm for Binary Multiplication using python - Divide and Conquer

In [1]:

import sys, os, random
import matplotlib.pyplot as plt
import numpy as np
sys.path.append("/home/swyoo/algorithm/")
from utils.verbose import logging_time, printProgressBar

Binary Multiplication

In [2]:

x,y = 3, 4
x = str(bin(x)[2:])
y = str(bin(y)[2:])
x, y

('11', '100')

Naive

One by one take all bits of second number and multiply it with all bits of first number.
Finally, add all multiplications. This algorithm takes $O(n^2)$ time.

Before implement naive binary-multiplication algorithm, let’s define some helper functions.

In [3]:

def fitlen(x, y):
    """ make x, y to become same length. 
    x and y are string, binary shape.  """
    m, n = len(x), len(y)
    if (m < n):
        x = '0' * (n - m) + x
    else:
        y = '0' * (m - n) + y
    return x, y

fitlen(x, y)

('011', '100')

Note that add(..) takes $O(n)$

In [4]:

def add(x, y):
    """ make x, y to become same length, and then add binary strings of x and y.
    x and y are string, binary shape. """
    if len(x) != len(y):
        x, y = fitlen(x, y)
    assert len(x) == len(y), "length is not same. "
    result = ""
    carry = 0
    for i in range(len(x) - 1, -1, -1):
        a = int(x[i])
        b = int(y[i])
        val = (a ^ b) ^ carry  # sum of (a,b,c) bits
        result = str(val) + result
        carry = (a & b) | (a & carry) | (b & carry)
    if carry:
        result = '1' + result
    return result

add('10', '11')

'101'

This is naive binary multiplication algorithm.
Naive multiplication takes \(O(n^2)\)

In [5]:

@logging_time
def naive(x, y, verb=False):
    """ given integer x, y. """
    # transform to same length strings.
    x, y = str(bin(x)[2:]), str(bin(y)[2:])
    if verb: print("multiply '0b{}' with '0b{}'".format(x, y))
    res = ""
    for k, j in enumerate(range(len(x) - 1, -1, -1)):
        tmp = ""
        for i in range(len(y) - 1, -1, -1):
            tmp = str(int(x[j]) * int(y[i])) + tmp
        tmp = tmp + '0' * k  # shift k to the left
        res = add(*fitlen(res, tmp))
    if verb: print("binary: {}".format(res))
    if verb: print("integer: {}".format(int(res, 2)))
    return res

In [6]:

naive(120, 3, verb=True)

multiply '0b1111000' with '0b11'
binary: 101101000
integer: 360

('101101000', 0.45371055603027344)

Karatsuba - Divide and Conquer

Assume that n is length of x, y, where we need to make x,y have same length.
We can use factorization of xy as follows \(x = x_{left} 2^{n/2} + x_{right} \\ y = y_{left} 2^{n/2} + y_{right}\)

\[(x_{left} 2^{n/2} + x_{right})(y_{left} 2^{n/2} + y_{right})\]

Key idea

• binary value x, y can be divided into left and right parts.
  • using factorization, recursively compute multiplication value. \(\begin{align} &(x_{l} 2^{n/2} + x_{r})(y_{l} 2^{n/2} + y_{r}) = x_l x_r 2^{n} + (x_l y_r + x_r y_l)2^{n/2} + y_l y_r \end{align}\) however, time complexity cannot be improved.
    This is becuase distinct 4 terms $x_l x_r, y_l y_r, x_l y_r, x_r y_l$ should be computed, and then add all as follows. \(\begin{align} &T(n) = 4T(n/2) + O(n) = O(n^2) \end{align}\)
• using a simple trick, we can use more efficient computation by reducing time complexity.
  • the trick as follows.
    \(\begin{align} & (x_l y_r + x_r y_l) = [(x_l + x_r)(y_l + y_r) - x_l y_l - x_r y_r] \end{align}\) by reusing $x_l y_l, x_r y_r$, the algorithm complexity is reduced. \(\begin{align} &T(n) = 3T(n/2) + O(n) = O(n^{log_23}) \end{align}\)

Implement $x_{left}$ as x[:n // 2] and $x_{right}$ as x[n // 2:].

x[:n // 2] has $\lfloor \frac{n}{2} \rfloor$ elements, x[n // 2:] has $\lceil \frac{n}{2} \rceil$ elements.

Therefore, $x = x_{left} 2^{\lceil \frac{n}{2} \rceil} + x_{right}$ because $x_{left}$ has $\lceil \frac{n}{2} \rceil$ elements.

E.g., we can divide a binary value x as follows.

In [7]:

x = str(bin(21)[2:])
n = len(x)
print(x)
print(x[:n//2],  x[n//2:])
# n // 2 means floor(n/2), n - n//2 means ceil(n/2)
print(x[:n//2] + '0' * (n - n//2), x[n//2:]) 
add(x[:n//2] + '0' * (n - n//2), x[n//2:])

10101
10 101
10000 101

'10101'

We can implement recursive formula as follows.

\[\begin{align} &(x_{l} 2^{2 \lceil \frac{n}{2} \rceil} + x_{r})(y_{l} 2^{\lceil \frac{n}{2} \rceil} + y_{r}) \\ &= x_l x_r 2^{2 \lceil \frac{n}{2} \rceil} + (x_l y_r + x_r y_l)2^{\lceil \frac{n}{2} \rceil} + y_l y_r \\ &= x_l x_r 2^{2 \lceil \frac{n}{2} \rceil} + [(x_l + x_r)(y_l + y_r) - x_l y_l - x_r y_r] 2^{\lceil \frac{n}{2} \rceil} + y_l y_r \end{align}\]

For the efficient computation, I implemented output as a integer value instead of string, binary value.
Please note that a simple computation of binary operation of integer in python as follows.

In [8]:

# 5 is "101" and 2^2 is muliplied by pusing '1' 2 times to the left.
print(5*(1 << 2)) # 0b101 concat 11 = 0b1011, which is 20, integer value
print(5*(1 << 3)) # 0b101 concat 111 = 0b10111, which is, integer value. 

20
40

In [9]:

@logging_time
def run(x, y):
    def multiply(x, y):
        """ given x and y are string, binary values.
        returns multiplied value as a integer. """
        x, y = fitlen(x, y)
        n = len(x)
        if n == 0: return 0
        if n == 1: return int(x) & int(y)
        assert n >= 2, "size error!"

        # len(xl): n // 2, len(xr): (n - n // 2)
        xl, xr = x[:n // 2], x[n // 2:]
        yl, yr = y[:n // 2], y[n // 2:]

        # each term is a integer.
        p1 = multiply(xl, yl)
        p2 = multiply(xr, yr)
        p3 = multiply(add(xl, xr), add(yl, yr))
        return p1 * (1 << 2 * (n - n // 2)) + (p3 - p1 - p2) * (1 << (n - n // 2)) + p2
    return multiply(x, y)

In [10]:

num_exp = 200
t1, t2 = [0]*num_exp, [0]*num_exp
sizes = list(np.linspace(start=10000, stop=1e+10, num=num_exp))
for i, size in enumerate(sizes):
    size = int(size)
    a, b = random.randint(size//5, size), random.randint(size//5, size)
    x, y = str(bin(a)[2:]), str(bin(b)[2:])
    gt = a * b
    ans1, t1[i] = naive(a, b)
    ans2, t2[i] = run(x, y)
    assert gt == int(ans1, 2) == ans2
    printProgressBar(iteration=i + 1, total=num_exp, msg="experiments...", length=50)

|██████████████████████████████████████████████████| 100.0 % - experiments...

In [11]:

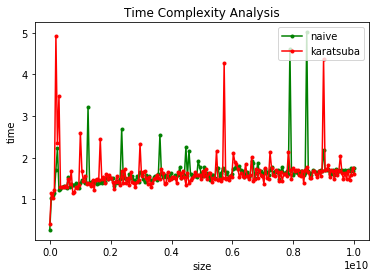
plt.xlabel('size')
plt.ylabel('time')
plt.title("Time Complexity Analysis")
plt.plot(sizes, t1, '.-g', label="naive")
plt.plot(sizes, t2, '.-r', label='karatsuba')
plt.legend(loc='upper right')
plt.show()

Reference

[1] geeksforgeeks
[2] report of uysalemre