In [1]:
1
2
3
4
5
import sys, string, random
sys.path.append('/home/swyoo/algorithm/')
from utils.verbose import logging_time, visualize_graph, visualize_ds
from typing import List
import numpy as np
1319. Number of Operations to Make Network Connected
In [2]:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution:
@logging_time
def makeConnected(self, n: int, connections: List[List[int]], show=False) -> int:
par, rnk = {}, {}
def find(x):
if x not in par:
par[x] = x
rnk[x] = 0
if x != par[x]:
par[x] = find(par[x])
return par[x]
def union(x, y):
x, y = find(x), find(y)
if x == y: return
if rnk[x] > rnk[y]:
x, y = y, x
par[x] = y
if rnk[x] == rnk[y]:
rnk[y] += 1
cnt = 0 # count the number of removable edges
for u, v in connections:
x, y = find(u), find(v)
if x != y:
union(x, y)
else:
cnt += 1
reps = 0 # number of representatives
for i in range(n):
if i == find(i):
reps += 1
if show:
print("------------- visualize disjoint set ----------------")
print("# of representavies: {}, # of counts: {}".format(reps, cnt))
visualize_ds(par)
print("-----------------------------------------------------")
return -1 if reps - 1 - cnt > 0 else reps - 1
sol = Solution()
In [3]:
1
2
3
4
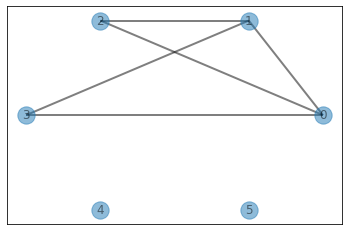
n = 6
connections = [[0,1],[0,2],[0,3],[1,2],[1,3]]
visualize_graph(connections, nodes=range(n), undirected=True)
print("ans: ", sol.makeConnected(n, connections, verbose=True, show=True))
1
2
3
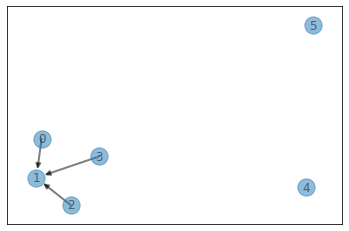
------------- visualize disjoint set ----------------
# of representavies: 3, # of counts: 2
1
2
3
4
-----------------------------------------------------
WorkingTime[makeConnected]: 166.85605 ms
ans: 2
In [4]:
1
2
3
4
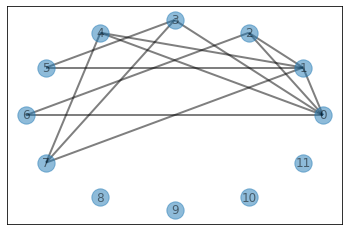
n = 12
connections = [[1,5],[1,7],[1,2],[1,4],[3,7],[4,7],[3,5],[0,6],[0,1],[0,4],[2,6],[0,3],[0,2]]
visualize_graph(connections, nodes=range(n), undirected=True)
print("ans: ", sol.makeConnected(n, connections, verbose=True, show=True))
1
2
3
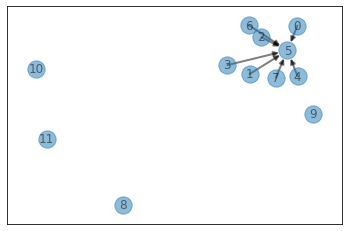
------------- visualize disjoint set ----------------
# of representavies: 5, # of counts: 6
1
2
3
4
-----------------------------------------------------
WorkingTime[makeConnected]: 184.37672 ms
ans: 4
Constraints:
1 <= n <= 10^51 <= connections.length <= min(n*(n-1)/2, 10^5)connections[i].length == 20 <= connections[i][0], connections[i][1] < nconnections[i][0] != connections[i][1]- There are no repeated connections.
- No two computers are connected by more than one cable.
In [7]:
1
2
3
4
5
6
7
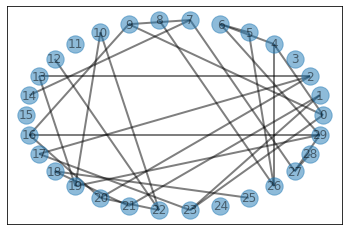
# a randomly generated graph
n, edges = 30, []
for i in range(n):
k = random.randint(0, (1 + n) // 15) # vertex 하나당 outgoing edge수 결정
edges.extend([(i, int(np.random.choice(list(range(i)) + list(range(i+1,n)), size=None))) for _ in range(k)])
visualize_graph(edges=edges, nodes=range(n), undirected=True)
print("ans: ", sol.makeConnected(n, edges, verbose=True, show=True))
1
2
3
------------- visualize disjoint set ----------------
# of representavies: 5, # of counts: 7

1
2
3
4
-----------------------------------------------------
WorkingTime[makeConnected]: 252.24304 ms
ans: 4
In [6]:
1
2
3
4
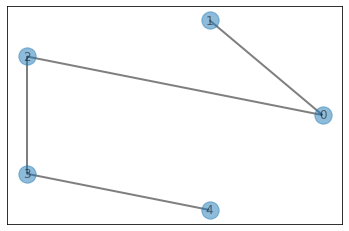
n = 5
connections = [[0,1],[0,2],[3,4],[2,3]]
visualize_graph(edges=connections, nodes=range(n), undirected=True)
print("ans: ", sol.makeConnected(n, connections, verbose=True, show=True))
1
2
3
------------- visualize disjoint set ----------------
# of representavies: 1, # of counts: 0
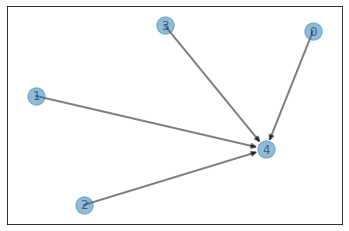
1
2
3
4
-----------------------------------------------------
WorkingTime[makeConnected]: 169.08622 ms
ans: 0


Leave a comment