How to implement Permutation in python

In [1]:

import sys
sys.path.append("/home/swyoo/algorithm/")
import random
from copy import deepcopy
from utils.verbose import logging_time
size = 3
a = list(range(size))
a

[0, 1, 2]

Permutation

Recursive Approach

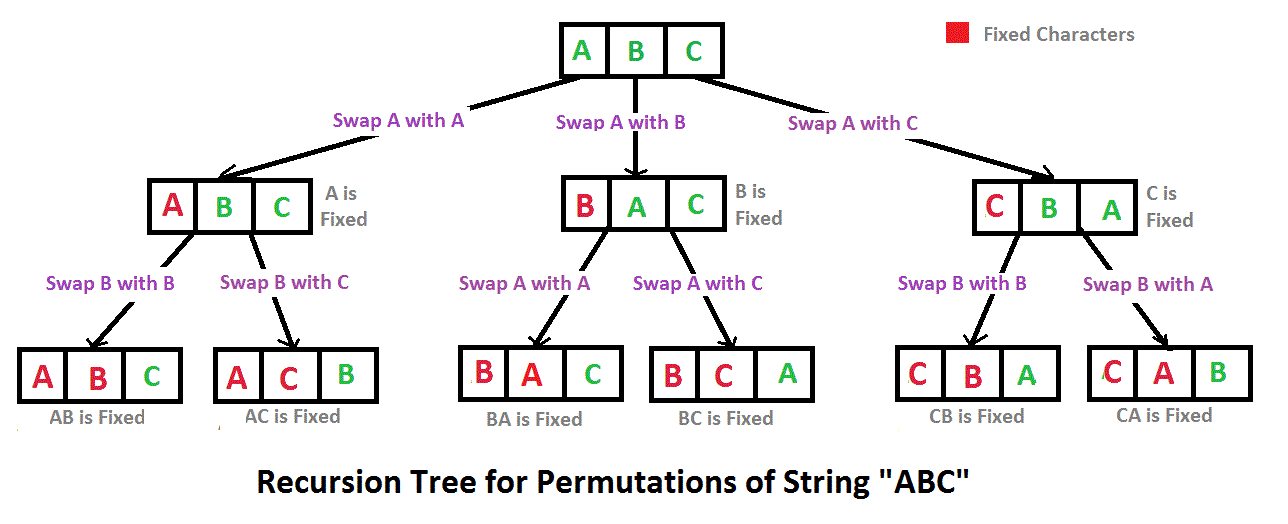
The time complexity is $O(nn!)$
Note that there are $n!$ permutations and it requires $O(n)$ time to print a a permutation.

In [2]:

@logging_time
def solution1(a):
    perms = []
    def f(s, e):
        if s == e:
            perms.append(deepcopy(a))
        for i in range(s, e + 1):
            a[i], a[s] = a[s], a[i]
            f(s + 1, e)
            a[i], a[s] = a[s], a[i]
    f(0, len(a) - 1)
    return perms
        
solution1(deepcopy(a), verbose=True)

WorkingTime[solution1]: 0.02956 ms

[[0, 1, 2], [0, 2, 1], [1, 0, 2], [1, 2, 0], [2, 1, 0], [2, 0, 1]]

Heap’s Algorithm

The time complexity of this algorithm is $O(n!)$.

In [3]:

@logging_time
def solution2(a):
    perms = []
    def f(size):
        if size == 1:
            perms.append(deepcopy(a))
            return
        
        for i in range(size):
            f(size - 1)
            if size & 1:  # odd
                a[0], a[size - 1] = a[size - 1], a[0]
            else:
                a[i], a[size - 1] = a[size - 1], a[i]
    f(len(a))
    return perms

solution2(deepcopy(a), verbose=True)

WorkingTime[solution2]: 0.02432 ms

[[0, 1, 2], [1, 0, 2], [2, 0, 1], [0, 2, 1], [1, 2, 0], [2, 1, 0]]

In [8]:

size = 9
a = list(range(size))
ans1 = solution1(deepcopy(a), verbose=True)
ans2 = solution2(deepcopy(a), verbose=True)

WorkingTime[solution1]: 2472.30506 ms
WorkingTime[solution2]: 2236.54580 ms

Library

itertools library provides us to get permutations easily.

In [11]:

from itertools import permutations

list(permutations(range(3), 2))

[(0, 1), (0, 2), (1, 0), (1, 2), (2, 0), (2, 1)]

Reference

[1] Korean Minusi’s blog
[2] Naive Permutation - geeksforgeeks
[3] Heap’s Algorithm - geeksforgeeks
[4] Permutation with Duplicates - geeksforgeeks