959.Regions Cut By Slash

Two Problems to make use of Disjoint Set(or Union Find)

In [1]:

from typing import List
from collections import defaultdict
import networkx as nx
import matplotlib.pyplot as plt
from networkx.drawing.nx_pylab import draw_networkx

In [2]:

def visualize(par):
    """ visualize disjoint set data structure. 
    :param: par: dictionary, which contains hierachical information of the disjoint set. """
    adj = defaultdict(list)
    edges = []
    for k, v in par.items():
        adj[k].append(v)
        edges.append((k, v))
    g = nx.DiGraph()
    g.add_edges_from(edges)
    # pos = nx.circular_layout(g)
    pos = nx.spring_layout(g, k=0.5, scale=10)
    draw_networkx(g, pos=pos, with_labels=True, width=2.0, alpha=0.5)
    plt.show()

959. Regions Cut By Slashes

I refered Youtube solution.
Given the size of $n \times n$ grid, the time complexity as follows.
(where $\alpha $ is the Inverse-Ackermann function.) \(O(n^2\alpha)\) The reasion is that
Disjoint datastructure is built in $O(N\alpha)$, where $N$ is the number of all nodes.
In this problem, the number of all nodes $N$ is $n^2$.

In [3]:

class Solution:
    def regionsBySlashes(self, grid: List[str], show=False) -> int:
        par, rnk = {}, {}

        def find(x):
            if x not in par:
                par[x] = x
                rnk[x] = 0
                return x
            if x != par[x]:
                par[x] = find(par[x])
            return par[x]

        def union(x, y):
            x, y = find(x), find(y)
            if x == y: return
            if rnk[x] > rnk[y]:
                x, y = y, x
            par[x] = y
            if rnk[x] == rnk[y]:
                rnk[y] += 1

        n = len(grid[0])
        for i, row in enumerate(grid):
            for j, c in enumerate(row):
                root = 4 * (i * n + j)
                if c != "/":
                    union(root, root + 2)
                    union(root + 1, root + 3)
                if c != "\\":
                    union(root, root + 1)
                    union(root + 2, root + 3)

                if i < n - 1:
                    union(root + 3, root + 4 * n)
                if i > 0:
                    union(root, root - 4 * n + 3)
                if j < n - 1:
                    union(root + 2, root + 4 + 1)
                if j > 0:
                    union(root + 1, root - 4 + 2)

        # count representatives
        ans = 0
        for x in range(4 * n * n):
            if x == find(x):
                ans += 1
        
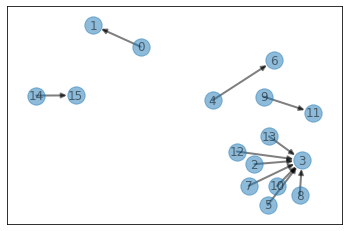
        if show:
            visualize(par)

        return ans
    
sol = Solution()

In [4]:

grid = \
    [
        "/\\",
        "\\/"
    ]
sol = Solution()
ans = sol.regionsBySlashes(grid, show=True)
print("ans: ", ans)

ans:  5

547. Friend Circles

Easy problem, which is similar with the first problem in leetcode

Given an array M, which means the information of friendship, where the size is $n$
such that

• M[i][i] = 1 for all students.
• M is symmetric

Union Find

Time complexity \(O(n^2\alpha)\)

In [5]:

class Solution1:
    def findCircleNum(self, M: List[List[int]], show=False) -> int:
        par, rnk = {}, {}

        def find(x):
            if x not in par:
                par[x] = x
                rnk[x] = 0
                return x
            if x != par[x]:
                par[x] = find(par[x])
            return par[x]

        def union(x, y):
            x, y = find(x), find(y)
            if x == y: return
            if rnk[x] > rnk[y]:
                x, y = y, x
            par[x] = y
            if rnk[x] == rnk[y]:
                rnk[y] += 1
        n = len(M[0])
        for i in range(n):
            for j in range(i, n):
                if M[i][j]:
                    union(i, j)
        if show:
            visualize(par)

        ans = 0
        for x in range(n):
            if x == find(x):
                ans += 1

        return ans
    
sol1 = Solution1()

In [6]:

""" generate an grid. """
import numpy as np
n = 32
rate = 0.96  # density of 0
tmp = np.random.choice(a=[False, True], size=(n, n), p=[rate, 1 - rate]).astype(int)
tmp = np.tril(tmp) + np.tril(tmp, -1).T
grid = (np.identity(n, dtype=bool).astype(int) | tmp).tolist()
# grid = \
# [[1,1,0],
#  [1,1,0],
#  [0,0,1]]

In [7]:

sol1 = Solution1()
ans1 = sol1.findCircleNum(grid, show=True)
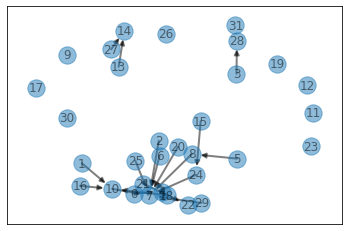
ans1

13

DFS

Idea:

• mark visted people by searching the friendship matrix.
• count starting dfs. \(O(n^2)\) This is because the algortihm sees each element only once.

In [8]:

class Solution2:
    def findCircleNum(self, M: List[List[int]]) -> int:
        n = len(M[0])
        seen = set()

        def dfs(start):
            seen.add(start)
            for j, direct in enumerate(M[start]):
                if direct and j not in seen:
                    dfs(j)
        ans = 0
        for i in range(n):
            if i not in seen:
                dfs(i)
                ans += 1
        return ans
    
sol2 = Solution2()

In [9]:

ans2 = sol2.findCircleNum(grid)
ans2

13

In [10]:

assert ans1 == ans2