Rod Cutting Problem - Dynamic Programming

In [1]:

import sys, random
import numpy as np
import matplotlib.pyplot as plt
sys.path.append("/home/swyoo/algorithm/")
from utils.verbose import logging_time, printProgressBar

Rod cutting

막대 길이에 대한 가격 $p[1..n]$ 이 주어졌을때, 최대한 비싸게 막대를 잘라서 팔아먹는 가격 $r_n$

cut을 한 경우과 안할 경우로 나누어 더 좋은것 선택 하면 다음과 같은 식으로 reculsive formula 가능 \(r_n = \max(p_n, \underset{1 \le i < n}{\max}{(r_i + r_{n-i})}) \text{, if } n \ge 1\)

$i=n$을 포함 시키고, $r_i$부분을 $ p_i$로 바꾸고, $ p_n +r_0 = p_n$으로 하면, 수식 간략화가 가능하다. \(\begin{aligned} r_n &= \begin{cases} \underset{1 \le i \le n}{\max}(p_i + r_{n-i}) & \text{if } n \ge 1 \\ 0 & \text{if } n = 0\\ \end{cases} \end{aligned}\)

In [2]:

INF = 1e+8
p = [-1,1,5,8,9,10,17,17,20,24,30] # p[0]은 더미 

top down

recursive top down 방식 ; inefficient
running time : \(T(n) = O(2^n)\)

In [3]:

# 길이 n 짜리 rod에 대해 cutting했을때의 최대 가격을 q로 저장 
@logging_time
def execute1(p, n):
    def cutrod(p, n):
        if n == 0:
            return 0
        q = -INF
        for i in range(1,n+1):
            q = max(q, p[i] + cutrod(p,n-i))  # 모든 경우를 계산하여  optimal 한경우를 q 로 저장 
        return q
    return cutrod(p, n)

In [4]:

ans, time = execute1(p, len(p)-1, verbose=True)
ans

WorkingTime[execute1]: 0.39840 ms

30

top down with memoization

checking 한 후(저장된 값이 있는지), 저장 값이 없다면 recursive call을 통해 subproblem 푼다.

running time: $ T(n) = O(n^2) $ ,because entry size n, choosing n => $ n^2 $

In [5]:

# top down with memoization 
# r[길이] array에 최대 가격을 메모한다. 

@logging_time
def execute2(p,n):
    # let r[0 .. n] be a new array 
    r = [0 for _ in range(n + 1)]
    
    for i in range(0,n+1):
        r[i] = -INF    # memo 할 r[i] 값을 초기화 한다. 
    return memo_topdown(p,n,r)  # r[] 에 memo를 하며 topdown 방식으로 문제를 푼다. 

#subroutine으로 이용
def memo_topdown(p,n,r):
    if r[n] >= 0:
        return r[n]
    
    if n == 0:
        return 0
        
    # 저장된값이 없다면,
    q = -INF
    for i in range(1,n+1):
        q = max(q, p[i] +  memo_topdown(p,n-i,r))    # 계산을 하여 최대값을 q로 지정 여기서 memo한것들은 O(1)시간에 된다.
            
    # 계산 후 저장        
    r[n] = q
    return q

In [6]:

ans, time = execute2(p, len(p)-1, verbose=True)
ans

WorkingTime[execute2]: 0.02885 ms

30

Bottom up

subproblem을 먼저 풀고, 이를 이용한다. memoization 을 통해 할 수 있다.

a problem of size is smaller than subproblem of size j ,if $ i \le j $

running time: $ T(n) = O(n^2) $ , because doubly nested loop $ i \le j \le n $

In [7]:

@logging_time
def execute3(p,n):
    # let r[0 .. n] be a new array 
    r = [None for _ in range(n + 1)]
    r[0] = 0
    
    # subproblem에서 부터 total sol을 이끌어낸다. 
    for j in range(1, n+1):
        q = -INF
        # i <= j 가 되도록 한다. 또한, r[j - i] 를 통해 subproblem의 solution을 이용 
        for i in range(1,j+1):
            q = max(q, p[i]+ r[j-i])  # Line 10~11 : subproblem size of j 를 푸는 과정(i = 1 .. j 경우의수에 대해 optimal값 찾음)
        r[j] = q
    return r[n]

In [8]:

ans, _ = execute3(p, len(p)-1, verbose=True)
ans

WorkingTime[execute3]: 0.02050 ms

30

In [9]:

num_exp = 50
t1, t2, t3 = [0]*num_exp, [0]*num_exp, [0]*num_exp
sizes = list(np.linspace(start=10, stop=25, num=num_exp))
for i, size in enumerate(sizes):
    size = int(size)
    p = [-1] + [random.randint(1,100) for _ in range(size)]
    ans1, t1[i] = execute1(p, size - 1)
    ans2, t2[i] = execute2(p, size - 1)
    ans3, t3[i] = execute3(p, size - 1)
    printProgressBar(iteration=i+1, total=num_exp, msg='experiment ...', length=50)

|██████████████████████████████████████████████████| 100.0 % - experiment ...

In [10]:

plt.xlabel('size')
plt.ylabel('time')
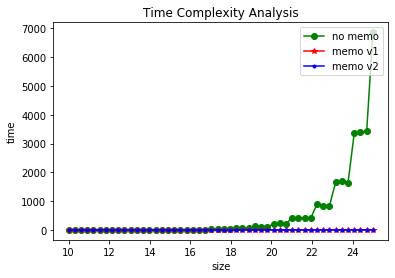
plt.title("Time Complexity Analysis")
plt.plot(sizes, t1, 'o-g', label="no memo")
plt.plot(sizes, t2, '*-r', label='memo v1')
plt.plot(sizes, t3, '.-b', label='memo v2')
plt.legend(loc='upper right')
plt.show()

In [11]:

plt.xlabel('size')
plt.ylabel('time')
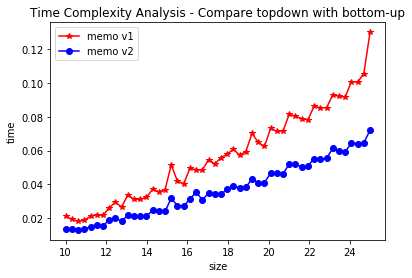
plt.title("Time Complexity Analysis - Compare topdown with bottom-up")
plt.plot(sizes, t2, '*-r', label='memo v1')
plt.plot(sizes, t3, 'o-b', label='memo v2')
plt.legend(loc='upper left')
plt.show()

Hw

Length | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

Price

1 5 8 9 10 17 17 20 24 25 25 30 32 33 35 37 37 40 42 43

1. 최대가 된 가격을 출력
2. 자른 막대의 길이를 출력 ex) (12, 5, 3) Hint) 1-D array 하나를 더 써서 가능

In [12]:

def extended_bottom_up_rod_cut(p,n):
    r = [0 for _ in range(n + 1)]   # r[] 배열의 초기값 
    s = [0 for _ in range(n + 1)]
    for j in range(1, n+1):
        q = -1
        for i in range(1, j+1):
            if q < p[i] + r[j-i]:
                q = p[i] + r[j-i]
                s[j] = i           # price 가 최대가 된 지점에서의 length i 를 s[j]에 저장
        r[j] = q                   # (j길이의 토막에서  i길이의 토막을 잘랐을때, 최대가됨)
        
    return r,s                    # r[j]에는 size j 의 토막 optimal price info 가 들어있고, 
                                  #s에는 r[j]를 만들때 i길이와 j-i 길이로 분해하는 값을 저장: s[j] = i 
                   
def print_cut_rod_solution(p,n):
    r,s = extended_bottom_up_rod_cut(p,n)
    while n > 0:
        print(s[n], end=" ")
        n = n - s[n]

In [13]:

p = [-1,1,5,8,9,10,17,17,20,24,25,25,30,32,33,35,37,37,40,42,43]
r,s = extended_bottom_up_rod_cut(p,(len(p)-1))
print(r)
print(s)

print("problem 1. ", (len(p)-1), "길이의 토막을 나눌때 최대가 된가격:  ", r[(len(p)-1)] )
print("problem 2.  ", "나무토막을 나눈 각각의 길이:", end=" ")
print_cut_rod_solution(p,(len(p)-1))

[0, 1, 5, 8, 10, 13, 17, 18, 22, 25, 27, 30, 34, 35, 39, 42, 44, 47, 51, 52, 56]
[0, 1, 2, 3, 2, 2, 6, 1, 2, 3, 2, 2, 6, 1, 2, 3, 2, 2, 6, 1, 2]
problem 1.  20 길이의 토막을 나눌때 최대가 된가격:   56
problem 2.   나무토막을 나눈 각각의 길이: 2 6 6 6 

Report

top down 방식은 recursive call에 대한 overhead 떄문에 bottom up 방식이 가장 빠르다.

ETC

c++ implementation

Reference