Detect Cycle using topolgoical sort python implementation

In [1]:

import sys, random
import numpy as np
import networkx as nx
from networkx.drawing.nx_pylab import draw_networkx
from collections import deque
import matplotlib.pyplot as plt

Generate a graph randomly

In [6]:

# generate a DAG
g = nx.DiGraph()
n, edges = 7, []
g.add_nodes_from(list(range(n)))
for i in range(n):
    k = random.randint(0, (1 + n) // 4) # vertex 하나당 outgoing edge수 결정
    edges.extend([(i, int(np.random.choice(list(range(i)) + list(range(i+1,n)), size=None))) for _ in range(k)])
g.add_edges_from(edges)
draw_networkx(g)
plt.savefig("./images/path.png")
print(g.nodes())
print(g.edges())

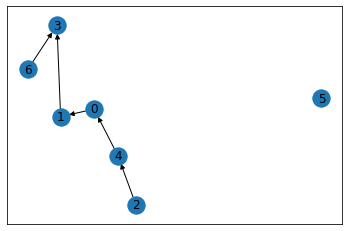
[0, 1, 2, 3, 4, 5, 6]
[(0, 1), (1, 3), (2, 4), (4, 0), (6, 3)]

In [12]:

# generate a graph with cycle
g2 = nx.DiGraph()
n, edges = 7, []
g2.add_nodes_from(list(range(n)))
for i in range(n):
    k = random.randint(0, (1 + n) // 4) # vertex 하나당 outgoing edge수 결정
    edges.extend([(i, int(np.random.choice(list(range(i)) + list(range(i+1,n)), size=None))) for _ in range(k)])
g2.add_edges_from(edges)
draw_networkx(g2)
plt.savefig("./images/path.png")
print(g2.nodes())
print(g2.edges())

[0, 1, 2, 3, 4, 5, 6]
[(0, 6), (1, 4), (2, 5), (3, 5), (4, 3), (5, 4), (6, 1), (6, 5)]

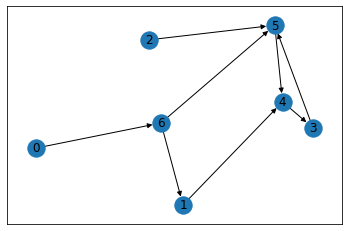
Detect Cycle in a DAG

어떤 그래프 g가 주어졌을때, cycle이 있는지 체크하는 것은 topological order를 구하다 보면 발견할 수 있다.
알고리즘을 공부했다면, 다음과 같은 사실을 이미 알고 있을 것이다.

그래프에 사이클이 존재한다면 topological sort를 할 수 없다.

DFS와 BFS를 이용하여 topological order를 구해보고, 그 과정에서 cycle이 있는지 체크하는 것을 구현해보자.

Use DFS

finish 할때 마다 stack에 쌓아 두면, 이 순서의 반대가 topological order를 의미한다.

dfs를 진행하다가 방문 한 적이 있는데(seen flag 가 True인데) finish 되지 않은 vertex를 방문한다면(finish flag가 False인 경우) cycle이 발생함을 의미한다.

이를 구현하기 위해서는 vertex 마다 finish 했는지 체크 할 수 있도록 한다.

Time complexity는 topolgical sort를 이용해서 모든 vertex와 edge를 한번만 보게 되므로 \(O(|V| + |E|)\)

no cycle

In [13]:

seen = [False] * n
finish = [False] * n
isDAG = True
topo = []
def detectCycle(g):
    """ check if g is DAG using DFS. """
    def dfs(g, i):
        global isDAG
        seen[i] = True
        print(i, end=" ")
        for j in g.adj[i]:
            if not seen[j]:
                dfs(g, j)
            elif not finish[j]: 
                print(j, end=" ")
                print("cycle exist!", end=" ")
                isDAG = False
                return 
            
        finish[i] = True
        topo.append(i)
    for i in range(n):
        if not seen[i]:
            dfs(g, i) 
            print("end")

detectCycle(g)
# if g is DAG, show topological order.
if isDAG:
    print("topolgical order:",)
    while topo:
        print(topo.pop(), end=" ")

0 1 3 end
2 4 end
5 end
6 end
topolgical order:
6 5 2 4 0 1 3 

cycle exist

In [14]:

seen = [False] * n
finish = [False] * n
isDAG = True
topo = []
detectCycle(g2)
# if g is DAG, show topological order.
if isDAG:
    print("topolgical order:",)
    while topo:
        print(topo.pop(), end=" ")

0 6 1 4 3 5 4 cycle exist! 5 cycle exist! end
2 5 cycle exist! end

---

In [17]:

draw_networkx(g)

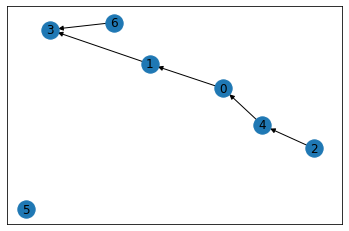
In [18]:

draw_networkx(g2)

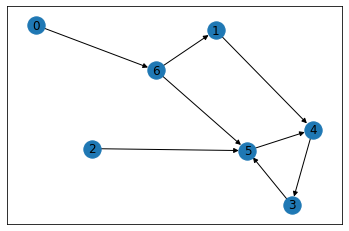
Use BFS

BFS를 이용하여 topological order를 구하는 과정은 다음과 같다.

• 각 vertex마다 indegree를 세어 놓는다.
• indegree가 0인 지점들은 topological order가 가장 앞선 지점들이므로 BFS의 시작지점들로 사용한다.
• bfs 통해 탐색하면서 outgoing edge들을 삭제해나간다(neighbor의 indegree를 낮춤).
  이때, indegree가 0이 되면 queue에 넣는다(topological order를 정할 때가 되었다는 것을 의미).

위의 과정을 따라가다보면 cycle이 없다는 가정하에 topological order가 앞선 vertex순으로 indegree가 0이 되면서 queue에 들어간다.

만약 cycle이 존재한다면 topological order가 앞서있는 vertex의 outgoing edge들을 삭제해도,
그 다음 topolgical order에 있는 indegree가 0이 되지않아 queue에 append 되지 않는다.
따라서, 모든 vertex를 한번씩 방문하기 전에 queue가 empty 상태가 되어 알고리즘이 종료된다.
(즉, 알고리즘 종료후 cnt 값이 n보다 작게 된다.)

Time complexity는 topolgical sort를 이용해서 모든 vertex와 edge를 한번만 보게 되므로 \(O(|V| + |E|)\)

no cycle

In [19]:

isDAG = True
cnt = 0
topo = []
def detectCycle(g):
    """ check if g is DAG using BFS. """
    indegree = [0] * n
    for i, j in g.edges():
        indegree[j] += 1
    print("indgree:", indegree)
    
    # starting points: points with indegree = 0
    st = [i for i in range(n) if indegree[i] == 0]
    print("starting points(preceding topo order): ", st)
    
    def bfs(g, st):
        global isDAG, cnt
        queue = deque(st)
        while queue:
            k = queue.popleft()
            topo.append(k)
            print(k, end=" ")
            for j in g.adj[k]:
                indegree[j] -= 1
                if indegree[j] == 0:
                    queue.append(j)
            cnt += 1 # vertex k가 finish 할때 count 증가
    bfs(g, st)
    isDAG = (cnt == n)
    return isDAG

if not detectCycle(g): print("cycle exist!")
else: print("\ntopo order is same with the visited order:", topo)

indgree: [1, 1, 0, 2, 1, 0, 0]
starting points(preceding topo order):  [2, 5, 6]
2 5 6 4 0 1 3 
topo order is same with the visited order: [2, 5, 6, 4, 0, 1, 3]

cycle exist

In [20]:

isDAG = True
cnt = 0
topo = []
if not detectCycle(g2): print("cycle exist!")
else: print("\ntopo order is same with the visited order:", topo)

indgree: [0, 1, 0, 1, 2, 3, 1]
starting points(preceding topo order):  [0, 2]
0 2 6 1 cycle exist!

Referenece

[1] geeksforgeeks - Use DFS
[2] geeksforgeeks - Use BFS
[3] korean blog