TRPO 코드분석

TRPO

제안한 surrogate objective function이 non-trival 한 step size로 policy improvement 를 보장함을 증명.

참조

설명
코드
코드설명

Pseudo-code

step 1: get returns and GAEs
step 2: train critic several steps with respect to returns
step 3: get gradient of loss and hessian of kl
step 4: get step direction and step size and full step
step 5: do backtracking line search for n times

---

optimization problem

\(\begin{align} \max_\theta\quad &E_{s\sim\rho_{\theta_\mathrm{old} },a\sim q}\left[\frac{\pi_\theta(a\vert s)}{q(a\vert s)}Q_{\theta_\mathrm{old} }(s,a)\right] \\ \mathrm{s.t.\ }&E_{s\sim\rho_{\theta_\mathrm{old} }}\left[D_\mathrm{KL}\left(\pi_{\theta_\mathrm{old} }(\cdot\vert s) \parallel \pi_\theta(\cdot\vert s)\right)\right] \leq \delta \end{align}\)

step 1 : get GAE

gae참조

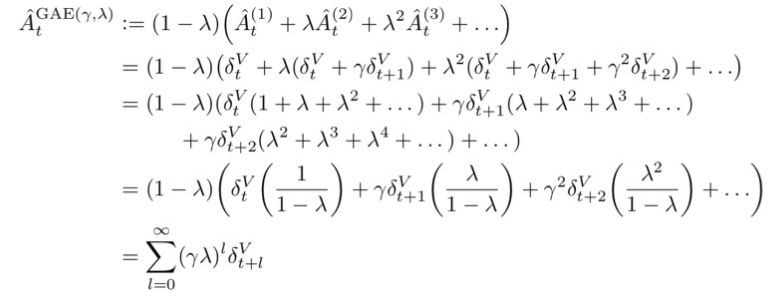
GAE는 td-error의 discounted summation

In [1]:

def train_model(actor, critic, memory, actor_optim, critic_optim):
    memory = np.array(memory)
    states = np.vstack(memory[:, 0])
    actions = list(memory[:, 1])
    rewards = list(memory[:, 2])
    masks = list(memory[:, 3])
    values = critic(torch.Tensor(states))

    # ----------------------------
    # step 1: get returns and GAEs
    returns, advants = get_gae(rewards, masks, values)

In [2]:

def get_gae(rewards, masks, values):
    rewards = torch.Tensor(rewards)
    masks = torch.Tensor(masks)
    returns = torch.zeros_like(rewards)
    advants = torch.zeros_like(rewards)

    running_returns = 0
    previous_value = 0
    running_advants = 0

    for t in reversed(range(0, len(rewards))):
        running_returns = rewards[t] + hp.gamma * running_returns * masks[t]
        running_tderror = rewards[t] + hp.gamma * previous_value * masks[t] - \
                    values.data[t]
        running_advants = running_tderror + hp.gamma * hp.lamda * \
                          running_advants * masks[t]

        returns[t] = running_returns
        previous_value = values.data[t]
        advants[t] = running_advants

    advants = (advants - advants.mean()) / advants.std()
    return returns, advants

step2 : train critic

Q의 MSE loss 를 구함

In [3]:

def train_model(actor, critic, memory, actor_optim, critic_optim):
    ...
    # ----------------------------
    # step 2: train critic several steps with respect to returns
    train_critic(critic, states, returns, advants, critic_optim)

In [4]:

def train_critic(critic, states, returns, advants, critic_optim):
    criterion = torch.nn.MSELoss()
    n = len(states)
    arr = np.arange(n)

    for epoch in range(5):
        np.random.shuffle(arr)

        for i in range(n // hp.batch_size):
            batch_index = arr[hp.batch_size * i: hp.batch_size * (i + 1)]
            batch_index = torch.LongTensor(batch_index)
            inputs = torch.Tensor(states)[batch_index]
            target1 = returns.unsqueeze(1)[batch_index]
            target2 = advants.unsqueeze(1)[batch_index]

            values = critic(inputs)
            loss = criterion(values, target1 + target2)
            critic_optim.zero_grad()
            loss.backward()
            critic_optim.step()

step 3: get gradient of loss and hessian of kl

In [5]:

def train_model(actor, critic, memory, actor_optim, critic_optim):
    ...

    # ----------------------------
    # step 3: get gradient of loss and hessian of kl
    mu, std, logstd = actor(torch.Tensor(states))
    old_policy = log_density(torch.Tensor(actions), mu, std, logstd)
    
    loss = surrogate_loss(actor, advants, states, old_policy.detach(), actions)
    loss_grad = torch.autograd.grad(loss, actor.parameters())
    loss_grad = flat_grad(loss_grad)
    step_dir = conjugate_gradient(actor, states, loss_grad.data, nsteps=10)

gradient of loss

\(\begin{equation} \begin{split} g &= \nabla_{\theta} L_{\theta_{old}(\theta)} |_{\theta_{old}} \\ &= \nabla_{\theta} E_{s\sim\rho_{\theta_\mathrm{old} },a\sim q}\left[\frac{\pi_\theta(a\vert s)}{q(a\vert s)}Q_{\theta_\mathrm{old} }(s,a)\right] \end{split} \end{equation}\)

In [6]:

def surrogate_loss(actor, advants, states, old_policy, actions):
    mu, std, logstd = actor(torch.Tensor(states))
    new_policy = log_density(torch.Tensor(actions), mu, std, logstd)
    advants = advants.unsqueeze(1)

    surrogate = advants * torch.exp(new_policy - old_policy)
    surrogate = surrogate.mean()
    return surrogate

changed constraint problem

\(\underset{\theta}{maximize}\; g^{T}s \;\; \mathrm{s.t. }\;\; \frac{1}{2}s^{T}Hs \leq \delta \;\;\mathrm{, where }\;\; s = \theta - \theta_{old}\)

Conjugate gradient method

update 방향 $s = H^{-1}g$ 를 효과적으로 찾는 방법

In [7]:

def conjugate_gradient(actor, states, b, nsteps, residual_tol=1e-10):
    x = torch.zeros(b.size())
    r = b.clone()
    p = b.clone()
    rdotr = torch.dot(r, r)
    for i in range(nsteps):
        _Avp = fisher_vector_product(actor, states, p)
        alpha = rdotr / torch.dot(p, _Avp)
        x += alpha * p
        r -= alpha * _Avp
        new_rdotr = torch.dot(r, r)
        betta = new_rdotr / rdotr
        p = r + betta * p
        rdotr = new_rdotr
        if rdotr < residual_tol:
            break
    return x

kl-divergence를 현재 policy에 대해서 구한 다음에 actor parameter에 대해서 미분.
이렇게 미분한 gradient를 일단 flat하게 핀 다음에 p라는 벡터와 곱해서 하나의 값으로 만듬

In [8]:

def fisher_vector_product(actor, states, p):
    p.detach()
    kl = kl_divergence(new_actor=actor, old_actor=actor, states=states)
    kl = kl.mean()
    kl_grad = torch.autograd.grad(kl, actor.parameters(), create_graph=True)
    kl_grad = flat_grad(kl_grad)  # check kl_grad == 0

    kl_grad_p = (kl_grad * p).sum()
    kl_hessian_p = torch.autograd.grad(kl_grad_p, actor.parameters())
    kl_hessian_p = flat_hessian(kl_hessian_p)

    return kl_hessian_p + 0.1 * p

step 4: get step size and full step

solution of changed optimization

\(\theta_{k+1} = \theta_{k} + \sqrt{\frac{2\delta}{s^{T}Hs}}s\)

In [9]:

def train_model(actor, critic, memory, actor_optim, critic_optim):
    ...

    # ----------------------------
    # step 4: get step direction and step size and full step
    params = flat_params(actor)
    shs = 0.5 * (step_dir * fisher_vector_product(actor, states, step_dir)
                 ).sum(0, keepdim=True)
    step_size = 1 / torch.sqrt(shs / hp.max_kl)[0]
    full_step = step_size * step_dir

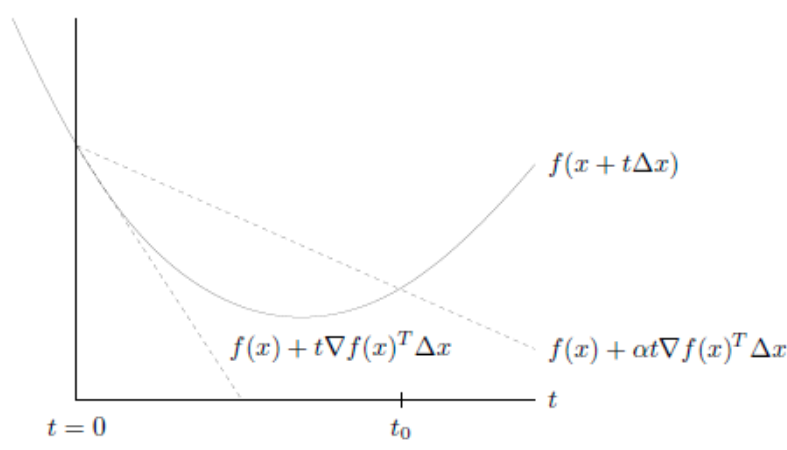
step 5: backtracking line search

실제 개선값 $f(x-t\nabla f(x))$ > 개선의 기대값 $f(x) - \alpha

\nabla f(x)

_{2}^{2}$

In [10]:

def train_model(actor, critic, memory, actor_optim, critic_optim):
    ...

    # ----------------------------
    # step 5: do backtracking line search for n times
    old_actor = Actor(actor.num_inputs, actor.num_outputs)
    update_model(old_actor, params)
    expected_improve = (loss_grad * full_step).sum(0, keepdim=True)

    flag = False
    fraction = 1.0
    for i in range(10):
        new_params = params + fraction * full_step
        update_model(actor, new_params)
        new_loss = surrogate_loss(actor, advants, states, old_policy.detach(),
                                  actions)
        loss_improve = new_loss - loss
        expected_improve *= fraction
        kl = kl_divergence(new_actor=actor, old_actor=old_actor, states=states)
        kl = kl.mean()

        print('kl: {:.4f}  loss improve: {:.4f}  expected improve: {:.4f}  '
              'number of line search: {}'
              .format(kl.data.numpy(), loss_improve, expected_improve[0], i))

        # see https: // en.wikipedia.org / wiki / Backtracking_line_search
        if kl < hp.max_kl and (loss_improve / expected_improve) > 0.5:
            flag = True
            break

        fraction *= 0.5

    if not flag:
        params = flat_params(old_actor)
        update_model(actor, params)
        print('policy update does not impove the surrogate')