Rewriting History with Inverse RL 리뷰

Rewriting History with Inverse RL 리뷰

제목: Rewriting History with Inverse RL: Hindsight Inference for Policy Improvement

Sergey Levin 이 쓴거면 인정

과거 경험들을 task를 나누어서 서로 다른 reward function으로 relabeling을 하는 것이 sample efficiency를 올릴 수 있다고 알려져 왔다. 이 논문에서는 위의 과정을 hindsight relabeling과정이라고 일컫고 그것은 결국 IRL과정임을 밝혔다. 그리고 단순히 success여부에 라서 정의된 discrete한 reward함수가 아닌 임의의 (linear) reward 함수들에 대해서 general 하게 적용되는 goal-relabeling technique을 제시하였다.

1. Introduction

1.1 이전 시도의 한계

multi-task RL이 single-task RL보다 sample-efficient한 이유는 학습을 위한 data를 공유하기 때문이다. 이전의 goal-relabeling task는 목표에 도달했는지 혹은 성공했는지를 heuristic하게 판단하여 discrete한 reward를 설정했기 때문에 효과적으로 relabeling 불가능 했다.

1.2 차이점

discrete한 reward에만 사용하는것이아니고 linear reward function과 같은 arbitrary reward function에도 적용가능한 방법을 제시했다.

1.3 Contribution

MaxEnt RL과 MaxEnt IRL은 동일한 Multi-task objective 를 최적화한다는 것을 증명했다.

RL은 높은 reward를 얻는 trajectory를 생성하도록 하는 것이고, IRL은 높은 reward를 얻는 task label을 찾는것이라는 관점에서

1.4 Idea

Hindsight Inference for Policy Improvement (HIPI) : IRL과정을 통해서 임의의 task distribution을 찾아서 relabeling을 하고 RL로 policy를 학습하자.

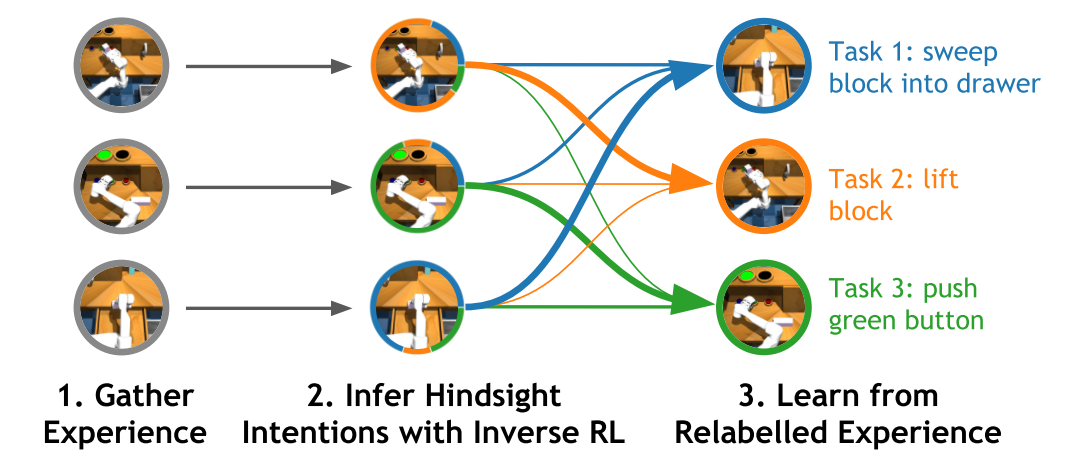
policy improvement과정에서 두가지 변형이 있다.

1. HIPI-RL : off-policy RL 방법론의 일종인 SAC을 사용
2. HIPI-BC: Supervised learning 방법의 일종인 task-conditioned Behavior-Cloning (BC)를 사용

2. Prior work

과거에는 A와 B 두가지 task가 있을 때 A task에 대한 experience data를 수집한 다음에 reward만 다시 계산해서 B task 를 학습하는데 사용했었다.

이전에는 task에 대한 posterior distribution을 찾는데 Maximum a-posterior(MAP) estimate 기법을 사용했다.

또한 MaxEnt IRL step 대한 inner loop로 MaxEnt RL step 를 사용했다.

저자는 반대로 MaxEnt RL step 대한 inner loop로 MaxEnt IRL step 를 사용한다.

MaxEnt RL 을 하기 위해서 KL divergence를 최소화한다. 저자는 이것을 multi-task 로 확장했다.

3. Preliminaries

MaxEnt RL와 MaxEnt IRL을 리뷰해보자.

3.1 Notation

policy $q$ 에 대한 trajectory $\tau$ 의 likelihood는 state-action sequence들의 joint distribution으로 아래와 같이 표기된다.

\[q(\tau) = p(s_1, a_1, s_2, \cdots ) = p_1(s_1) \underset{t}{\Pi}p(s_{t+1}|s_t, a_t) q(a_t| s_t)\]

그리고 각 task를 $\psi \in \Psi$ 로, task에 대한 reward function을 $r_{\psi}(s_t,a_t)$ 로 표기한다.

3.2 MaxEnt RL

experience sample을 사용하여 RL formulation을 통해 학습할 때 exploring start라는 가정 때문에 exploration이 부족하여 local minima에 빠져서 해를 구하지 못할 수도 있다.

이 문제를 해결하기 위해서 학습하는 policy에 높은 disorder를 주어서 탐험하지 못한 영역도 탐험할 수 있도록 학습하는 방법을 제시한 것이 MaxEnt RL이다. optimize식은 entropy regularized sum of reward를 최대화 하는 식이며 아래와 같다.

\[\underset{p(\tau)}{Max}\bigg[\mathbb{E}[\sum_{t}\gamma^{t}r(s_t,a_t)] - \alpha p(\tau)\log p(\tau)\bigg]\]

위의 식은 soft bellman function을 통해서 수렴성이 증명되었고, 해가 아래와 같이 reward에 대한 지수족으로 나온다는 것을 보였다. 위의 부분에 좀더 알고 싶다면 Reinforcement Learning with Deep Energy-Based Policies 논문을 참고하여 soft q-learning에 대해서 알아보자.

\[p(\tau) = \frac{e^{r(\tau)}}{\int_{} e^{r(\tau)}d\tau} = \frac{e^{r(\tau)}}{Z}\]

이때, 우리가 구하고 싶은 해인 target distribution $p(\tau)$는 아래와 같다.

\[p(\tau) = \frac{1}{Z} p_1(s_1) \underset{t}{\Pi} p(s_{t+1}|s_t, a_t) e^{r(s_t,a_t)}\]

여기서 Z 는 partition function으로 $p(\tau)$ 를 적분했을 때 1로 만드는 normalization을 위한 항이고 sequence 성분을 분해하여 표현하면 아래와 같다.

\[Z \triangleq \int p_1(s_1) \underset{t}{\Pi} p(s_{t+1}|s_t, a_t) e^{r(s_t,a_t)} d\tau\]

우리는 학습하고 있는 policy를 rollout해서 얻은 trajectory에 대한 policy distribution $q(\tau)$ 이 target distribution $p(\tau)$ 과 동일하게 만드는 것을 목표로 한다. 그래서 두 분포의 kl divergence를 최소화하는 방법으로 학습이 가능하다. 그 말은 즉 음의 kl divergence를 최대화하는 것과 동일하다.

\[\require{cancel} \begin{split} -D_{KL}(q(\tau)|| p(\tau))) &= \mathbb{E}_{q}[\log\frac{p(\tau)}{q(\tau)}] \\ &= \mathbb{E}_{q}[\log \frac{\frac{1}{Z} \cancel{p_1(s_1)} \underset{t}{\Pi} \cancel{p(s_{t+1}|s_t, a_t)} e^{r(s_t,a_t)}} { \cancel{p_1(s_1)} \underset{t}{\Pi} \cancel{p(s_{t+1}|s_t, a_t)} q(a_t| s_t)}] \\ &= \mathbb{E}_{q}[(\sum_{t} r(s_t, a_t) - \log q(a_t |s_t)) - \log Z] \end{split}\]

여기서 partition function $Z$ 은 가능한 모든 trajectory에 대해서 적분을 해야하기 때문에 large space에서는 계산이 intractable할 수 있다. 하지만 위의 식에서 Z는 학습하는 policy $q(a_t|s_t)$ 에 무관한 항이기 때문에 최적화 과정에서는 계산할 필요없이 상수로 취급할 수 있다. \(\underset{q}{Max} \mathbb{E}_{q}[(\sum_{t} r(s_t, a_t) - \log q(a_t |s_t)) - \cancel{ \log Z}]\)

3.3 MaxEnt IRL

IRL과정은 이전에 수집된 데이터를 사용해서 reward function $r_{\psi}$ 로 표현된 actor의 intent 를 추론하고자 하는 방법이다.

하지만 IRL의 formulation으로 reward function을 찾게 되면 unique한 solution이 존재하지 않고 large set의 해가 구해져서 Degeneracy 문제가 있다. 이때 ambiguous policy를 유발하게 되는데 이 문제를 해결하기 위해서 여러 policy 중에서 가장 entropy가 큰 policy를 사용하겠다는 아이디어로 제시한 것이 MaxEnt IRL이다. 우리가 관측할 수 있는 것은 likelihood 로 task $\psi$ 에 대해서 생성된 trajectory들이다.
Target likelihood $p(\tau | \psi)$ 은 MaxEnt RL과 동일한 맥락으로 entropy regularized sum of reward를 최대화하여 구할 수 있고 해는 아래와 같다.

\[p(\tau | \psi) = \frac{1}{Z(\psi)} p_1(s_1) \underset{t}{\Pi} p(s_{t+1}|s_t, a_t) e^{r_{\psi}(s_t,a_t)} \\ ,where \; Z(\psi) \triangleq \int p_1(s_1) \underset{t}{\Pi} p(s_{t+1}|s_t, a_t) e^{r_{\psi}(s_t,a_t)} d\tau\]

하지만 우리가 구하고자하는 것은 posterior 다른 말로 relabeling distribution이다. Target relabeling distribution은 Bayes’ rule에 의해 아래와 같이 구할 수 있다.
\(\begin{split} p(\psi | \tau) &= \frac{p(\tau | \psi) p(\psi)}{p(\tau)} \\ &= \frac{p(\psi) \frac{1}{Z(\psi)} \cancel{p_1(s_1)} \underset{t}{\Pi} \cancel{p(s_{t+1}|s_t, a_t)} e^{r_{\psi}(s_t,a_t)}} {\frac{1}{Z} \cancel{p_1(s_1)} \underset{t}{\Pi} \cancel{p(s_{t+1}|s_t, a_t)} e^{r(s_t,a_t)}} \\ &\propto p(\psi) e^{\underset{t}{\sum} r_{\psi}(s_t,a_t) - \log Z(\psi)} \end{split}\)

여기서 MAP를 적용하면 식은 아래와 같다.

\[\underset{\psi}{Argmax} [\log p(\psi| \tau)]\]

여기서 partition function $Z$ 은 모든 state-action pair에 대해서 적분을 계산해야 해서 large space에서 intractable하다. 그런데 위의 식에 대한 dual 표현은 MaxEnt RL 문제와 동일하다. 어떻게 그러한 결론이 나왔는지 살펴보자.

사실 partition function은 unknown reward function과 optimal policy로 부터 induced 되었다. 따라서 Z의 해는 unknown reward function 의 지수족으로 표현된다. 우리는 optimal policy 모르니까 proposal policy $q$ 를 도입하여 sample 평균을 내서 아래와 같이 $Z$를 근사하고 proposal policy를 여러번 rollout하여 구한 proposal distribution $q( \tau)$ 에 대한 최적값으로 Z를 구할 수 있다. 위의 과정으로 구한 MaxEnt IRL과정은 MaxEnt RL 식과 동일하다.

\[\begin{split} Z(\psi) &\approx E_{\tau \sim q(\tau|\psi)} [\frac{e^{\underset{t}{\sum} r_{\psi}(s_t, a_t)}} {\underset{t}{\Pi} q(a_t | s_t, \psi)} ] \\ Z(\psi) &= \underset{q(\tau | \psi)}{Max} \bigg[ E_{\tau \sim q(\tau|\psi)} [\frac{e^{\underset{t}{\sum} r_{\psi}(s_t, a_t)}} {\underset{t}{\Pi} q(a_t | s_t, \psi)} ] \bigg] \\ \log Z(\psi) &= \underset{q(\tau | \psi)}{Max} \bigg[ E_{\tau \sim q(\tau|\psi)} [ \underset{t}{\sum} r_{\psi}(s_t, a_t) - \log q(a_t | s_t, \psi)] \bigg] \end{split}\]

​

4. Hindsight Relabeling is Inverse RL

이번 섹션에는 MaxEnt RL과 MaxEnt IRL이 동일하게 task $\psi$ 와 trajectory $ \tau$ 의 joint distribution에 대해서 아래와 같이 reverse KL Divergence를 minimize한다는 것을 보일 것이다. 우선 MaxEnt RL의 경우 아래의 최적화식을 푸는 문제이다.

\[\underset{q(\tau, \psi)}{Max} -D_{KL}(q(\tau, \psi) || p(\tau, \psi)) \\\]

위의 식에서 $q(\psi)$ 는 $p(\psi)$ 와 같다는 가정하에 $q(\tau, \psi)$ 와 $p(\tau, \psi)$ 를 factorize 하면 아래와 같다.

\[\begin{split} q(\tau, \psi) &= q(\psi) q(\tau | \psi) \\ &= p(\psi) q(\tau | \psi) \\ &=p(\psi) p(s_1, a_1, s_2, \cdots |\psi) \\ &= p(\psi) p_1(s_1) \underset{t}{\Pi}p(s_{t+1}|s_t, a_t) q(a_t| s_t, \psi) \\ p(\tau, \psi) &= p(\psi) p(\tau | \psi) \\ &= \frac{p(\psi)}{Z(\psi)} p_1(s_1) \underset{t}{\Pi} p(s_{t+1}|s_t, a_t) e^{r_{\psi}(s_t,a_t)} \end{split}\]

다시 optimization식을 정리하면 아래와 같다.

\[\begin{split} -D_{KL}(q(\tau, \psi) || p(\tau, \psi)) &= \mathbb{E}_{\psi \sim q(\psi),\\ \tau \sim q(\tau| \psi)} [\log \frac{p(\tau, \psi)} {q(\tau, \psi)}] \\ &= \mathbb{E}_{\psi \sim q(\psi),\\ \tau \sim q(\tau| \psi)} [ \log \frac{\frac{\cancel{p(\psi)}}{Z(\psi)} \cancel{p_1(s_1)} \underset{t}{\Pi} \cancel{p(s_{t+1}|s_t, a_t)} e^{r_{\psi}(s_t,a_t)}} {\cancel{p(\psi)} \cancel{p_1(s_1)} \underset{t}{\Pi} \cancel{p(s_{t+1}|s_t, a_t)} q(a_t| s_t, \psi)} \\ &= \mathbb{E}_{\psi \sim q(\psi),\\ \tau \sim q(\tau| \psi)} [(\sum_{t} r_{\psi}(s_t, a_t) - \log q(a_t |s_t, \psi)) - \log Z(\psi)] \end{split}\]

최적화 과정에서 $Z(\psi)$ 는 $q(\tau | \psi)$ 에 무관하므로 아래와 같이 3.2절의 최종식과 동일한 형태이다.

\[\begin{split} \underset{q(\tau, \psi)}{Max} & -D_{KL}(q(\tau, \psi) || p(\tau, \psi)) \\ &= \underset{q(\tau, \psi)}{Max} \mathbb{E}_{\psi \sim q(\psi),\\ \tau \sim q(\tau| \psi)}[\sum_{t} r_{\psi}(s_t, a_t) - \log q(a_t |s_t, \psi)] \end{split}\]

​

그런데 위 식에서 문제점은 우리는 $q(\psi)$ 를 알 수 없다는 점이다.
그래서 $q(\tau, \psi) = q(\tau) q(\psi | \tau)$ 로 factorize하여 구할 수 있다.

\[\begin{split} -D_{KL}(q(\tau, \psi) || p(\tau, \psi)) &= \mathbb{E}_{\tau \sim q(\tau),\\ \psi \sim q(\psi| \tau)} [\log \frac{p(\tau, \psi)} {q(\tau) q(\psi | \tau)}] \\ &= \mathbb{E}_{\tau \sim q(\tau),\\ \psi \sim q(\psi| \tau)} [\log \frac{\frac{p(\psi)}{Z(\psi)} p_1(s_1) \underset{t}{\Pi} p(s_{t+1}|s_t, a_t) e^{r_{\psi}(s_t,a_t)}} {q(\tau) q(\psi | \tau)}] \\ &= \mathbb{E}_{\tau \sim q(\tau),\\ \psi \sim q(\psi| \tau)} \bigg[ \log p_1(s_1) +\underset{t}{\sum} \bigg( r_{\psi}(s_t,a_t) + \log p(s_{t+1}|s_t, a_t)\bigg) \\ &+ \log p(\psi) - \log q(\psi | \tau) - \log q(\tau) -\log Z(\psi) \bigg] \end{split}\]

저자의 아이디어를 적용하려면 optimal relabeling distribution을 찾으면 된다. 위의 식에서 task $\psi$ 와 무관한 항을 상수 취급하고 소거하여 최적화하면 아래와 같다.

\[\begin{split} -D_{KL}(q(\tau, \psi) || p(\tau, \psi)) &= \mathbb{E}_{\tau \sim q(\tau),\\ \psi \sim q(\psi| \tau)} \bigg[ \cancel{\log p_1(s_1)} +\underset{t}{\sum} \bigg( r_{\psi}(s_t,a_t) + \cancel{\log p(s_{t+1}|s_t, a_t)}\bigg) \\ &+ \log p(\psi) - \log q(\psi | \tau) - \cancel{\log q(\tau)} -\log Z(\psi) \bigg] \\ &= \mathbb{E}_{\tau \sim q(\tau),\\ \psi \sim q(\psi| \tau)} \bigg[ \underset{t}{\sum} r_{\psi}(s_t,a_t) + D_{KL}(q(\psi | \tau)|| p(\psi)) -\log Z(\psi) \bigg] \\ q(\psi|\tau) &= \underset{q(\psi|\tau)}{Argmax}\Bigg[ \mathbb{E}_{\tau \sim q(\tau),\\ \psi \sim q(\psi| \tau)} \bigg[ \underset{t}{\sum} r_{\psi}(s_t,a_t) + D_{KL}(q(\psi | \tau)|| p(\psi)) -\log Z(\psi) \bigg] \Bigg] \\ &\propto p(\psi) e^{\underset{t}{\sum} r_{\psi}(s_t,a_t) - \log Z(\psi)} \end{split}\]

위의 과정으로 부터 task에 대한 MaxEnt RL 식으로 부터 구한 optimal relabeling distribution $q(\psi | \tau)$ 이 task에 대한 MaxEnt IRL posterior인 target relabeling distribution $p(\psi | \tau)$ 과 정확히 일치한하는 것을 알 수 있다.

그러므로 우리는 IRL step으로 optimal relabeling distribution을 얻을 수 있다.

우리는 soft-Q-function을 도입하여 trajectory가 아닌 한개의 state action pair에 대한 optimal relabeling distribution $q(\psi | s_t, a_t)$ 를 구할 수 있다.

아래와 같이 MaxEnt RL의 objective에 policy distribution $q$ 에 한개의 state-action-pair $(s_t, a_t)$ 조건을 추가하면 된다. 이때 $q(\tau, \psi | s_t, a_t) = q(\psi | s_t,a_t) q(\tau | \psi, s_t, a_t)$ 로 factorize한다.

\[\begin{split}q(\tau, \psi |s_t, a_t) &= q(\psi|s_t,a_t)q(\tau|\psi,s_t,a_t) \\ &= q(\psi|s_t,a_t) p(s_1, a_1, s_2, \cdots |\psi,s_t,a_t) \\ &= q(\psi|s_t,a_t) p_1(s_1) \underset{t'}{\Pi}p(s_{t'+1}|s_{t'}, a_{t'}) q(a_{t'}| s_{t'}, \psi) \\ p(\tau, \psi) &= p(\psi) p(\tau | \psi) \\ &= \frac{p(\psi)}{Z(\psi)} p_1(s_1) \underset{t'}{\Pi}p(s_{t'+1}|s_{t'}, a_{t'}) e^{r_{ \psi}(s_{t'},a_{t'})} \end{split}\]

위에서 정리한 식을 다시 objective function에 대입하고 soft-q-function을 도입하면 아래와 같다.

\[\begin{split} -D_{KL}(q(\tau, \psi | s_t, a_t) || p(\tau, \psi)) &= \mathbb{E}_{\psi \sim q(\psi|s_t,a_t) \\ \tau \sim q(\tau|\psi,s_t,a_t)} [\log \frac{p(\tau, \psi)} {q(\psi|s_t,a_t)q(\tau|\psi,s_t,a_t)}] \\ &= \mathbb{E}_{\psi \sim q(\psi|s_t,a_t) \\ \tau \sim q(\tau|\psi,s_t,a_t)} [\log \frac{\frac{p(\psi)}{Z(\psi)} \cancel{p_1(s_1)} \underset{t'}{\Pi} \cancel{p(s_{t'+1}|s_{t'}, a_{t'})} e^{r_{\psi}(s_{t'},a_{t'})}} {q(\psi|s_t,a_t)\cancel{p_1(s_1)} \underset{t'}{\Pi} \cancel{p(s_{t'+1}|s_{t'}, a_{t'})} q(a_{t'}| s_{t'}, \psi)}] \\ &= \mathbb{E}_{\psi \sim q(\psi|s_t,a_t) \\ \tau \sim q(\tau|\psi,s_t,a_t)} \bigg[ \underset{t'}{\sum} \bigg( r_{\psi}(s_{t'},a_{t'}) - \log q(a_{t'}| s_{t'}, \psi)\bigg) \\ &+ \log p(\psi) - \log q(\psi|s_t,a_t) -\log Z(\psi) \bigg] \\ &= \tilde{Q}^{q}(s_t,a_t,\psi) + \mathbb{E}_{\psi \sim q(\psi|s_t,a_t) \\ \tau \sim q(\tau|\psi,s_t,a_t)} [ D_{KL}(q(\psi | s_t, a_t) || p(\psi)) -\log Z(\psi) ] \\ ,where \; \tilde{Q}^{q}(s_t,a_t,\psi) =& \mathbb{E}_{\psi \sim q(\psi|s_t,a_t) \\ \tau \sim q(\tau|\psi,s_t,a_t)} \bigg[ \underset{t'}{\sum} r_{\psi}(s_{t'},a_{t'}) - \log q(a_{t'}| s_{t'}, \psi) \bigg] \end{split}\]

위의 식에서 task $\psi$ 와 무관한 항을 상수 취급하고 소거하여 최적화하여 한개의 state-action pair에 대한 optimal relabeling distribution을 찾으면 아래와 같다.

\[\begin{split} q(\psi|s_t,a_t) &= \underset{q(\psi|s_t,a_t)}{Argmax}\Bigg[ \tilde{Q}^{q}(s_t,a_t,\psi) + \mathbb{E}_{\psi \sim q(\psi|s_t,a_t) \\ \tau \sim q(\tau|\psi,s_t,a_t)} [ D_{KL}(q(\psi | s_t, a_t) || p(\psi)) -\log Z(\psi) ] \Bigg] \\ &\propto p(\psi) e^{ \tilde{Q}^{q}(s_t,a_t,\psi) - \log Z(\psi)} \end{split}\]

4.1 Special Case: Goal Relabeling

이번 섹션에서는 prior relabeling 방법이 IRL의 special case임을 보인다.

아래와 같이 goal-state 를 $\psi$로 두고 goal conditioned reward function을 정의했다고하면,

\[r_{\psi}(s_t,a_t) = \begin{cases} -\infty & if & t=T & and & s_t \neq \psi \\ 0 & otherwise \end{cases}\]

labeling distribution은 terminal state에서 goal 도달 여부에 따른 indicator function이된다.

\(q(\psi| \tau) = \mathbb{1}(\psi = s_T)\) 즉 위의 경우처럼 MaxEnt IRL formulation에서 특정 reward 함수를 사용하면 task들에 대해서 relabeling 을 해주는 판별기를 만들 수 있다는 것을 보였다.

​

4.2 The Importance of the Partition Function

이번 섹션에서는 partition function을 사용해서 task에 대한 reward를 normalize해주는 것이 어떠한 효과를 가져오는지 보여준다.

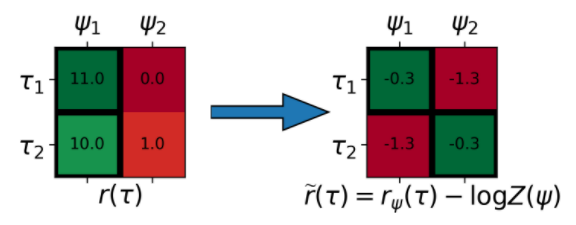
왼쪽 그림은 task conditioned reward function의 스케일이 다를 때 발생하는 문제를 보여준다. task1 의 reward scale이 task2 보다 너무 커버린 경우이다. 검정색 박스가 각 경로를 labeling한 결과를 나타내는데 모든 경로가 task 1으로 되어 버리게 된다.

오른쪽 그림에서 reward를 task 가 같은 각 경로의 대소관계를 유지하면서 즉 row 방향으로 scale을 조절하면 column 방향으로 비교가 제대로 이루어져서 각 경로마다 올바르게 task을 비교하면서 할당을 할 수 있다.

4.3 How much does relabeling help?

이번 섹션에서는 original data를 가지고 계산한 target joint distribution 과의 KL divergence와 max entropy-regularized reward로 구한 optimal relabeling distribution으로 relabeling된 data를 가지고 계산한 target joint distribution 과의 KL divergence를 비교했을 때 improvement가 되는 것을 보였다.

다시말해 lemma1에서는 optimal relabeling distribution improvement 를 증명한다.

그리고 lemma2에서는 두 kl divergence 차이의 lower bound를 구해서 최소 어느 정도의 성능을 개선하는 지를 보인다.

그러므로 lemma 1과 2로 수렴성을 수학적으로 보였다.

4.3.1 lemma 1

relabeled distribution이 original distribution보다 더 target distribution에 가까워 진다.

\[D_{KL}(q_{\tau}(\tau, \psi) || p(\tau, \psi)) \leq D_{KL}(q(\tau, \psi) || p(\tau, \psi))\]

최초 task $\psi$ 와 trajectory $\tau$ 의 joint distribution $q(\tau, \psi)$은 policy $q(a_t | s_t, \psi)$ 로 rollout 을 해서 얻는다. 이후 trajectory distribution 은 joint distribution은 marginalize하여 다음과 같이 구할 수 있다.

\[q_{\tau}(\tau) = \int q(\tau, \psi)\]

아래와 같이 optimal relabeling distribution $q_{\tau}(\psi |\tau)$ 를 구하고 marginal distribution $q_{\tau}(\tau)$ 를 relabeling하여 relabeled distribution $q_{\tau}(\tau, \psi)$을 구한다.

\[q_{\tau}(\tau, \psi) = q_{\tau}(\psi|\tau)q_{\tau}(\tau)\]

위의 과정에 따라서 initial relabeling distribution 을 $q_{0}(\psi| \tau)$ 라고 하면,

$q(\tau, \psi) = q_{0}(\psi| \tau)q_{\tau}(\tau)$ 이고,

\[q_{\tau}(\psi\|\tau) = \underset{q(\psi\|\tau)}{Argmin} D_{KL}[q(\tau, \psi) \|\| p(\tau, \psi)]\]

이기 때문에 아래와 같은 식이 성립한다.

\[D_{KL}( q_{\tau}(\psi|\tau)q_{\tau}(\tau) || p(\tau, \psi)) \leq D_{KL}( q_{0}(\psi|\tau)q_{\tau}(\tau) || p(\tau, \psi))\]

4.3.2 lemma 2

relabeled distribution과 original distribution의 target distribution과의 차이에 대한 성능 향상의 lower bound는 다음과 같다.

\[D_{KL}(q(\tau, \psi) || p(\tau, \psi)) - D_{KL}(q_{\tau}(\tau, \psi) || p(\tau, \psi)) \geq \underset{q_{\tau}\in Q_{\tau}}{\mathbb{E}} \bigg[ D_{KL}(q(\psi | \tau) || q_{\tau}(\psi | \tau)) \bigg] \\ ,where \; Q = \{q(\tau, \psi) \;s.t \; \int q(\tau, \psi) d\psi = q_{\tau}(\tau) \} \\ ,where \; Q_{\tau} = \{q_{\tau}(\tau) \;s.t \; \int q(\tau, \psi) d\psi = q_{\tau}(\tau) \}\]

증명과정은 아래와 같다. kl divergence의 삼각부등식으로 부터 출발한다.

\[D_{KL}(q(\tau, \psi) || p(\tau, \psi)) \geq D_{KL}(q_{\tau}(\tau, \psi) || p(\tau, \psi)) + D_{KL}(q(\tau, \psi) || q_{\tau}(\tau, \psi))\]

위의 식에서 $D_{KL}(q(\tau, \psi) | | q_{\tau}(\tau, \psi))$ 는 아래와 같이 분해되어 정리 할 수 있다.

\[\begin{split} D_{KL}(q(\tau, \psi) || q_{\tau}(\tau, \psi)) &= D_{KL} \bigg[ q(\psi|\tau)q_{\tau}(\tau)|| q_{\tau}(\psi|\tau)q_{\tau}(\tau) \bigg] \\ &= \int q(\psi|\tau)q_{\tau}(\tau) \log \frac {q(\psi|\tau) \cancel{q_{\tau}(\tau)} } {q_{\tau}(\psi|\tau) \cancel{q_{\tau}(\tau)} } \\ &= \int q_{\tau}(\tau) q(\psi|\tau)\log \frac {q(\psi|\tau) } {q_{\tau}(\psi|\tau) } \\ &=\underset{q_{\tau}(\tau)}{\mathbb{E}} \bigg[ D_{KL}[q(\psi | \tau) || q_{\tau}(\psi | \tau)] \bigg] \end{split}\]

5. Using Inverse RL to Accelerate RL

relabeled experience에 대해서 policy improvement를 하는 방법에서 저자는 두가지 variant를 제시한다.

첫번째는 off-policy RL method인 SAC을 사용하는 HIPI-RL이고,

두번째는 BC을 하는 HIPI-BC이다.

알고리즘은 아래와 같다.

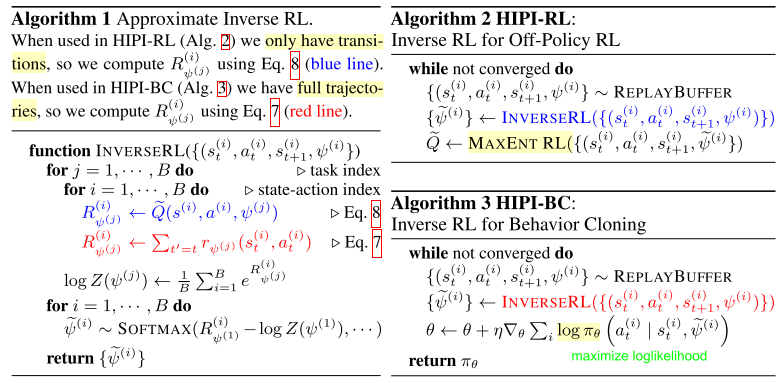
5.1 Using Relabeling Data for Off-Policy RL (HIPI-RL)

off-policy RL을 적용하기 위해서 partition function을 아래와 같이 experience replay buffer에서 추출한 Monte carlo sample $(s_i,a_i)$ 로 부터 근사화하여 구한다.

\[\begin{split} \log Z(\psi) &= \log \int e^{\tilde{Q}(s_t,a_t,\psi)}dsda \\ &= \log \int e^{R_{\psi}(s_t,a_t)}dsda \\ & \approx \frac{1}{B} \sum^{B}_{i=1}R_{\psi}(s^{(i)},a^{(i)}) \end{split}\]

​

이후 아래와 같은 labeling distribution을 사용하여 task 를 sample하고 다시 relabeling하여 buffer에 저장한다.

\[q(\psi^{(i)}|s^{(i)},a^{(i)}) \propto e^{R_{\psi}(s^{(i)},a^{(i)}) - \log \tilde{Z}(\psi^{(i)})}\]

5.2 Using Relabeled Data for Behavior Cloning

relabeled된 trajectory로 부터 바로 policy 를 implicit하게 추출해내는 방법이다.

objective 는 아래와 같다.

\[\begin{split} &\int q(\psi| \tau) \underset{t}{\sum}\log \pi(a_t|s_t, \psi) d\psi d\tau \\ &= \int e^{R_{\psi}(s_t,a_t) - \log Z(\psi) } \underset{t}{\sum}\log \pi(a_t|s_t, \psi) d\psi d\tau \end{split}\]

이전 방법들과의 차이는 partition function의 존재이다.