Fuel Cost Optimization ProblemPermalink
In [1]:
1
2
3
4
import numpy as np
import matplotlib.pyplot as plt
import cvxpy as cp
cp.__version__
1
'1.1.7'
Initialization of system dynamics and hyper parameterPermalink
Let x(t)x(t) be state and u(t)u(t) be input.
-
Fuel cost funtion follows like this:
f(a)={|a|,|a|≤12|a|−1,|a|>1 -
Totol fuel cost follows like this:
F=∑N−1t=1f(u(t)) -
System dynamics follows like this:
- Optimization problem can be defined as follows:
In [2]:
1
2
3
4
5
6
n = 3 # state dim
N = 30 # time horizon
A = np.array([[-1, 0.4, 0.8],[1, 0, 0],[0, 1, 0]])
B = np.array([1, 0, 0.3]).reshape(n,1)
x0 = np.zeros(shape=(n,1))
xdes = np.array([7, 2, -6]).reshape(n,1)
Problem Definition and Finding solution with cvxpyPermalink
In [3]:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def cost(a):
x = cp.abs(a)
y = 2 * cp.abs(a) - 1
out = cp.max(cp.vstack([x,y]))
return out
x = cp.Variable(shape=(n,N+1))
u = cp.Variable(shape=(1,N))
total_cost = 0
constr = []
for t in range(N):
total_cost += cost(u[:,t])
constr += [x[:,t+1] == A@x[:,t] + B@u[:,t]]
constr += [x[:,0] == x0[:,0], x[:,N] == xdes[:,0]]
# constr = x[:,1:N+1] == A@x[:,0:N] + B@u
prob = cp.Problem(cp.Minimize(total_cost), constraints=constr)
prob.solve()
# Print result.
print("\nThe optimal cost is", prob.value)
print("The optimal input is")
print(u.value)
1
2
3
4
5
6
7
8
9
10
11
12
The optimal cost is 17.323567851898538
The optimal input is
[[ 3.29220286e-11 4.43409588e-11 -4.10965143e-09 1.00000000e+00
-1.00000000e+00 1.00000000e+00 -1.22937435e-10 3.52557537e-12
9.97638379e-11 -9.99999999e-01 1.00000000e+00 -1.00000000e+00
2.46624155e-01 -4.48381061e-11 -1.94767993e-11 2.97961922e-10
-1.00000000e+00 1.00000000e+00 -9.99999999e-01 2.60644166e-10
-4.11865495e-12 -3.22199860e-11 1.00000000e+00 -6.98881472e-01
1.00000000e+00 -9.33641505e-11 2.85325077e-09 1.19009817e-10
1.13195663e-11 3.18903111e+00]]
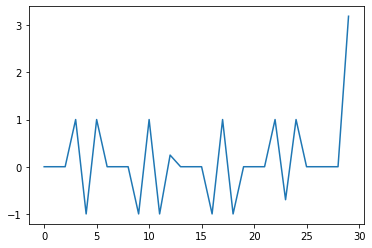
Plot desired inputPermalink
In [4]:
1
2
input_values = u.value.flatten()
plt.plot(range(N), input_values)
1
[<matplotlib.lines.Line2D at 0x7f56a649f1d0>]
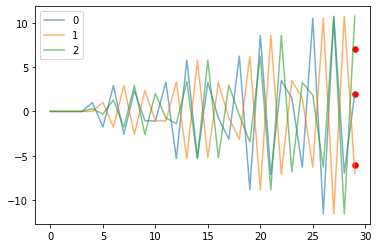
Plot state transition along desired inputPermalink
In [31]:
1
2
3
4
5
6
7
8
9
inputs = u.value
outputs = np.zeros(shape=(n,N))
for t in range(N-1):
outputs[:,t+1] = np.matmul(A,outputs[:,t]) + np.matmul(B,inputs[:,t])
for i in range(n):
plt.plot(range(N), outputs[i,:], label=str(i),alpha=0.6)
plt.scatter(29, xdes[i],color='r',s=30)
print(outputs[:,29])
plt.legend()
1
2
[ 2. -6.95670933 10.74206578]
1
<matplotlib.legend.Legend at 0x7f569e0731d0>
Leave a comment