Inequality Summary

Inequality Summary

Markov’s Inequality¹

Markov’s inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant.

If $X$ is a nonnegative random variable and $a > 0$, then the markov’s inequality as follows. \(P(X \ge a ) \le \frac{\mathbb{E}(X)}{a}\)

Intuitive proof

\[\begin{align} \mathbb{E}(X) &= P(X < a) \cdot \mathbb{E}(X \vert X < a) + P(X \ge a) \cdot \mathbb{E}(X \vert X \ge a) \\ &\ge P(X < a) \cdot 0 + P(X \ge a) \cdot a &\text{since }X \text{ is positive r.v} \\ &\ge P(X \ge a) \cdot a \end{align}\]

Meaning

Markov’s inequality (and other similar inequalities) relate probabilities to expectations, and provide (frequently loose but still useful) bounds for the cumulative distribution function of a random variable.

Chebyshev’s Inequality

Chebyshev’s inequality uses the variance to bound the probability.

The inequality as follows for $a > 0$.
\(P(\vert X - \mathbb{E}(X)\vert \ge a) \le \frac{Var(X)}{a^2}\)

Intuitive proof

\[\begin{align} P(\vert X - \mathbb{E}(X) \vert \ge a) &=P((X - \mathbb{E}(X))^2) \ge a) \\ &\le \frac{\mathbb{E}[(X - \mathbb{E}(X))^2]}{a^2} = \frac{Var(X)}{a^2} & \text{from Markov's inequality} \\ \end{align}\]

Meaning

let $a = \tilde{a}\sigma$ where $\sigma = \sqrt{Var(X)}$, chebyshev’s inequality is transformed as follows. \(P(\vert X - \mathbb{E}(X)\vert \ge \tilde{a} \sigma) \le \frac{1}{\tilde{a}^2}\) The above formula means that samples according to any random distribution can be close to mean.

This is because the probability of going $\tilde{a}$ times the standard deviation further from the mean is less than $\frac{1}{\tilde{a}^2}$.

Chernoff Bounds²

Chernoff bound gives exponentially decreasing bounds on tail distributions of sums of independent random variables, which is sharper bound than Markov’s inequality or Chebyshev’s inequality.

If $X$ is a random variable, then $\forall t \in \mathbb{R}$, the chernoff bound is as follows. \(\begin{align} P(X \ge a) &\le \frac{\mathbb{E}[e^{t\cdot X}]}{e^{t\cdot a}} &\forall t>0 \\ P(X \le a) &\le \frac{\mathbb{E}[e^{t\cdot X}]}{e^{t\cdot a}} &\forall t<0 \end{align}\)

Therefore, \(\begin{align} P(X \ge a) &\le \underset{t > 0}{min} \frac{\mathbb{E}[e^{t\cdot X}]}{e^{t\cdot a}} \\ P(X \le a) &\le \underset{t < 0}{min} \frac{\mathbb{E}[e^{t\cdot X}]}{e^{t\cdot a}} \end{align}\)

intuitive proof

for $t > 0$ \(\begin{align} P(X \ge a) &= P(e^{t \cdot X} \ge e^{t \cdot a}) \\ &\le \frac{\mathbb{E}[e^{t \cdot X}]}{e^{t \cdot a}} &\text{by Markov's inequality}\\ \end{align}\)

for $t < 0$ \(\begin{align} P(X \le a) &= P(e^{t \cdot X} \ge e^{t \cdot a}) \\ &\le \frac{\mathbb{E}[e^{t \cdot X}]}{e^{t \cdot a}} &\text{by Markov's inequality}\\ \end{align}\)

I found an Example 6.22 in a course³ to compare between Markov, Chebyshev, and Chernoff Bounds.

Let $X \sim Binomial(n, p)$, find upper bounds on $P(X \ge \alpha n)$, where $p=\frac{1}{2}, \alpha = \frac{3}{4}$.

Moment Generating Function is as follows. \(M_X(t) \triangleq \mathbb{E}[e^{t\cdot X}]\) For $X \sim Binomial(n, p)$, $M_X(t) = (p e^t + q)^n$ where $q = 1 - p$.

Proof \(\begin{align} M_X(t) &= \sum_{x=0}^n e^{tx} \frac{n!}{x!(n-x)}p^xq^{n-x} \\ &= \sum_{x=0}^n (pe^{t})^x \frac{n!}{x!(n-x)}q^{n-x} \\ &= (pe^t + q)^n \end{align}\)

For $X \sim Binomial(n, p)$, \(\begin{align} \mathbb{E}[X] &= np = \frac{n}{2}\\ Var(X) &= np(1-p) = \frac{n}{4} \\ \end{align}\)

At first, Markov’s bound is as follows. \(P(X \ge \frac{3}{4}n) \le \frac{4}{3n}\mathbb{E}[X] = \frac{4}{3n} \times \frac{n}{2} = \frac{2}{3}\) Second, Chebyshev’s bound is as follows. \(\begin{align} P(X \ge \frac{3}{4}n) &= P(X - \mathbb{E}[X] \ge \frac{n}{4}) &\text{ since } \mathbb{E}[X]= \frac{n}{2}\\ &\le \frac{16}{n^2}Var(X) = \frac{16}{n^2}\times \frac{n}{4} = \frac{4}{n} \end{align}\) Finally, Chernoff bound is as follows. \(P(X \ge \frac{3}{4}) \le \underset{t > 0}{min}\frac{\mathbb{E}[e^{t\cdot X}]}{e^{t\cdot a}} = (\frac{16}{27})^{\frac{n}{4}}\)

Proof \(\begin{align} \frac{\partial}{\partial t} M_X(t) &= \frac{\partial}{\partial t}(pe^t + q)^n = npe^{t}(pe^t + q)^{n-1} = 0 \\ e^s& =\frac{aq}{np(1 - \alpha)} \end{align}\)

Hoeffding’s Inequality and Lemma⁴

Hoeffding’s Inequality

Hoeffding’s inequality provides an upper bound on the probability that the sum of bounded independent random variables deviates from its expected value by more than a certain amount.

Hoeffding’s inequality is a generalization of the Chernoff bound.

Let $X_1, \cdots , X_n$ be independent bounded random variables with $X_i \in [a_i, b_i]$ for all $i$, where $-\infty < a_i \le b_i < \infty$. Hoeffding’s inequality is as follows for $t \ge 0$.

\[\begin{align} \bar{X} &= \frac{1}{n}(X_1 + X_2 + \cdots + X_n)\\ P(\bar{X} - \mathbb{E}[\bar{X}] \ge t) &\le exp(-\frac{2n^2t^2}{\sum_{i=1}^n(b_i - a_i)^2}) \\ &\text{and} \\ P(\bar{X} - \mathbb{E}[\bar{X}] \le -t) &\le exp(-\frac{2n^2t^2}{\sum_{i=1}^n(b_i - a_i)^2})\\ \end{align}\]

The Hoeffding’s inequality can be proved using (1) Chernoff bounds and (2) Hoeffding’s lemma.

Hoeffding’s Lemma

Suppose $X$ is a random variable such that $P(X \in [a, b]) = 1$. Then \(\begin{align} \mathbb{E}[e^{t(X - \mathbb{E}[X])}] &\le exp(\frac{1}{8}t^2(b - a)^2) &\forall t \in \mathbb{R} \end{align}\)

Jensen’s Inequality

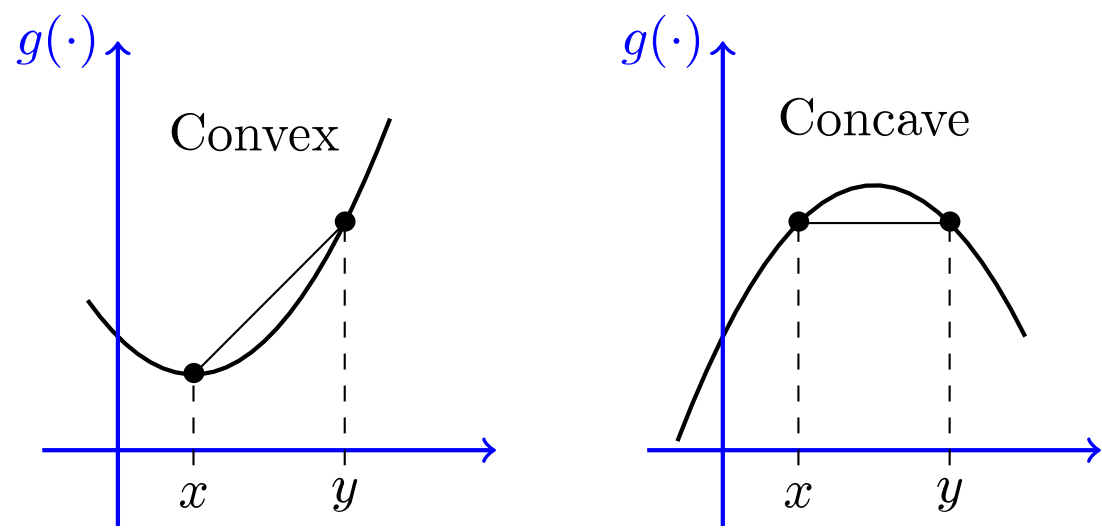
Reference

---

Appendix

Central Limit Theorem

The central limit theorem (CLT) establishes that, in many situations, when independent random variables are added, their properly normalized sum tends toward a normal distribution even if the original variables themselves are not normally distributed.

Let $\bar{X}_n$ be sample mean and $\mu$ be the ideal mean.

From CLT, if $n \rightarrow \infty$, then

$\sqrt{n}(\bar{X}_n - \mu) \sim N(0, \sigma^2)$ where $\sigma$ is ideal standard deviation.

Alternatively, $\bar{X}_n \sim N(\mu, \frac{\sigma^2}{n})$.

Notice this fact as follows when $\bar{X}_n$ is converged. \(\begin{align} X_i &\sim N(n\mu, n\sigma^2) &\text{ since } \bar{X_n} = \frac{1}{n}\sum_{i=1}^n X_i \\ \end{align}\)

1. https://en.wikipedia.org/wiki/Markov%27s_inequality “markov inequality” ↩

2. https://en.wikipedia.org/wiki/Chernoff_bound “chernoff bounds” ↩

3. https://www.probabilitycourse.com/ “See Chap6 > 6.2 Secsion” ↩

4. https://en.wikipedia.org/wiki/Hoeffding%27s_inequality “hoeffding inequality” ↩