sw Yoo

sw Yoo

No sweat, no sweet

Contents

Sort

Dynamic Programming

Greedy

Graph

Sort

c++ python

Insertion sort

incremental하게 하나씩 원소를 삽입하며 정렬하는 방식

즉, $j$ 번째 이전에 이미 정렬되어있는 상태에서 $A_j$를 삽입한후 제자리를 찾아가는 방식

1
2
3
4
5
6
7
8
9
10
11

insert(A, j, key)
	i = j - 1
    while i > 0 and A[i] > key
    	A[i+1] = A[i]
        i = i - 1
    A[i+1] = key
    

IS(A)
    for j = 2 to n 
        insert(a, j, a[j])

blog

Quicksort (increasing order)

qs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

QS(a, p, r)
	if p >= r
		return
	# select random btw p ~ r
	i = random(p,r)
	swap(a[i], a[r]) # 무조껀 뒤로 보냄
	
	# partition
	i = p - 1
	for j = p to r-1
		if a[j] <= a[r]
			i += 1
			swap(a[j], a[i])
    swap(a[i+1], a[r])
    q = i + 1 # a[q] finds a right position
    
    # divide and conquer
    QS(a, p, q-1)
    QS(a, q+1, r)

randomized quick sort가 아닐 경우 worst case time complexity

i 번째 원소에서 분할이 될 때 점화식은 다음과 같다.

$T(n) = T(i-1) + T(n-i) + O(n)$

최악의 경우 $i = 1 \,or \,n$ 이고 다음과 같다.

$T(n) = T(n-1) + O(n)$

반복대치를 통해 시간복잡도를 구해보자 \(\cancel{T(0)} = 0\\ \cancel{T(1)} = \cancel{T(0)} + O(1)\\ \cancel{T(2)} = \cancel{T(1)} + O(2)\\ ...\\ T(n) = \cancel{T(n-1)} + O(n)\\ -------------\\ T(n) = O(1)\, + \,...\, + \,O(n) = O(n^2)\)

proof by mathmatical induction 방법을 통해 randomized quicksort 의 expected time complextiy 증명 \(Suppose \;\exist c \;s.t\; T(k) \le ck\log{k} \;\forall \;2\le k <n\) $T(n) = T(i-1) + T(n-i) + O(n)$ 에서 i는 1 부터 n 중에서 uniform하게 선택되기 때문에 \(\begin{matrix} T(n) &=& \frac{1}{n}\sum_{i=1}^n {T(i-1) + T(n-i)} + O(n)\\ &=& \frac{2}{n}\sum_{k=0}^{n-1}T(k) + O(n)\\ &=& \frac{2}{n}\sum_{k=2}^{n-1}T(k) + \{O(0) + O(1) + O(n)\}\\ &\le& \frac{2}{n}\sum_{k=2}^{n-1}ck\log{k} + O(n)\leftarrow 가정\\ &\le& \frac{2}{n}\sum_{k=1}^{n-1}ck\log{k} + O(n)\\ &=& \frac{2c}{n}\{\sum_{k=1}^{[\frac{n}{2}]-1}k\log{k} + \sum_{k=[\frac{n}{2}]}^{n-1}k\log{k}\} + O(n)\\ &\le& \frac{2c}{n}\{\sum_{k=1}^{[\frac{n}{2}]-1}k\log{\frac{n}{2}} + \sum_{k=[\frac{n}{2}]}^{n-1}k\log{n}\} + O(n)\leftarrow \sum_{k=1}^{[\frac{n}{2}]-1}\log{k} \le \log{\frac{n}{2}}이므로\\ &=& \frac{2c}{n}\{\sum_{k=1}^{[\frac{n}{2}]-1}k(\log{n} - 1) + \sum_{k=[\frac{n}{2}]}^{n-1}k\log{n}\} + O(n)\\ &=& \frac{2c}{n}\{\log{n}\sum_{k=1}^{n-1}k - \sum_{k=1}^{[\frac{n}{2}]-1}k\} + O(n)\\ &\le& \frac{2c}{n}\{\log{n}\frac{n(n-1)}{2} - \frac{1}{2}(\frac{n}{2}- 1)(\frac{n}{2})\} + O(n) \leftarrow [\frac{n}{2}] \le \frac{n}{2} 이므로 \\ &=& c(n\log{n} -\log{n} - \frac{n}{8} + \frac{n}{4}) + O(n)\\ &=& O(n\log{n}) \end{matrix}\)

다른방식으로 expected running time $O(nlogn)$ 증명

intuition: quick sort에서 parition 은 $O(n)$ 번 불리게 되어있다. 이때, qicksort의 성능은 pivot이 어디 선택되어 partition 내부 안에서 비교 횟수가 몇번 불리느냐에 달려있다. 모든 $n$ 번의 patition에서 비교 횟수가 불리는 수의 합을 $X$ 라 하면, time complexity는 $O(n+X)$ 이다.

그래서 call 되는 patition 함수들 안에서 비교되는 횟수의 합의 평균 $E[X] $가 성능을 좌우한다. 이 값을 구하기위해 그 안에서 정렬된 숫자를 ${z_i, …,z_j}$ 라고 하면,

picture

그리고, $E[X]$를 estimate하기위해 i.i.d. $ X_{ij} = 1$ (if $z_i$ is compared to $z_j$, o.w., 0) 를 정의하면 ($P[$ $z_i$ is compared with $z_j] = P_{ij}$ 라 하자, iid 특성은 평균값이 확률값과 같음)

$E[X] = E[\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}X_{ij}] = \sum_{i=1}^{n-1}\sum_{j=i+1}^{n}E[X_{ij}] = $ $\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}$$P_{ij}$ 이되는데,

picture

위의 그림으로 부터 알 수 있는 것은, 서로 다른 partition에 있는 $z_i$ 와 $z_j$ 는 절대 비교 안된다는 사실로부터 partition 함수 안에 $z_i$, $z_j$ 가 있어야하며 둘중 하나는 반드시 pivot이 될것 이라는 사실이다. 따라서, $j-i+1$ element 중 $z_i, z_j$가 각각 pivot으로 뽑힐 확률인 $P_{ij} = 2/(j-i+1)$ 이다.

다시 되돌아가서, 계산해보면, $\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}$$2/(j-i+1)$ $\le \sum_{i=1}^{n} \sum_{i \le j}{2/j} = O(nlogn)$

더 나아가서 …

r.f. 항상좋은 quick sort 방법은? median of median 이용 link

quickselect c++

Mergesort

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

Merge(A, p, q, r)
    n1 = q - p + 1
    n2 = r - q
    let L[1 .. n1 + 1] and R[1 ..n2 + 1] be new arrays
    for i = 1 to n1 
        L[i] = A[p + i - 1]
    for j = 1 to n2 
        R[j] = A[q + j]
    L[n1 + 1] = Inf
    R[n2 + 1] = Inf
    i,j = 1
    for k = p to r
        if L[i] <= R[j]
            A[k] = L[i]
            i += 1
        else
            A[k] = R[j]
            j += 1

MS(A, p, r)
    if p >= r 
        return
    q = (p + r) / 2;
    MS(A, p, q);
    MS(A, q + 1, r);
    Merge(A, p, q, r);

time complexity

마스터정리를 사용하여 시간복잡도를 구해보자. \(T(n) = 2 T(\frac{n}{2}) + O(n)\\ f(n) = O(n)\\ h(n) = n^{\log_{2}{2}} = O(n) = f(n)\\ \therefore T(n) = O(n\log{n})\)

Heapsort

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

# increasing order sort를 위한 max heap 을 기준으로 설명
heapify(A, i) 
    left = 2i
    right = 2i + 1
    
    if right > n 
    	return
    
    # find largest among A[i], A[left], A[right]
    if A[i] < A[left]
    	largest = left
    else 
    	largest = i 
    if A[largest] < A[right]
    	largest = right
    
    swap(A[i], A[largest])
    
    if largest != i
    	heapify(A, largest)

# bottom up 
build_heap(A)	
	A.heapsize = |A|
    for i = A.length / 2 downto 1 
    	heapify(i) 
        
# divide and conquer
make_heap(A, i)
    left = 2i
    right = 2i + 1
    
    if right > n
    	return 
    
    make_heap(left)
    make_heap(right)
    
    if A[i] < A[left]
    	largest = left 
    else largest = i
    if A[largest] < A[right]
    	largest = right
    
    swap(A[i], A[largest])
    
    if largest != i 
    	heapify(A, largest)
        
HS(A)
	build_heap(A)
	for i = |A| downto 2 
    	swap(A[1], A[i])
        A.heapsize -= 1
        heapify(A,1)

heapify: $T(n) = T(n/2) + 1 = O(logn)$

build_heap: $T(n) = 2T(n/2) + O(logn)$ \(n^{log_2^2} > logn \\ \therefore T(n) = O(n)\) divide conquer 를 통한 build heap c++

Dynamic Programming

divide and conquer(recursive call, top down) 에서 memo를 하면 DP 가 된다.

따라서 크게 top down with memo, bottom up 2가지 접근법

DP를 사용하려면 Optimal substructure, Overlapping subproblem 2가지 성질을 증명해야함

python

Rod cutting

막대 길이에 대한 가격 $p[1..n]$ 이 주어졌을때, 최대한 비싸게 막대를 잘라서 팔아먹는 가격 $r_n$

cut을 한 경우과 안할 경우로 나누어 더 좋은것 선택 하면 다음과 같은 식으로 reculsive formula 가능 $r_n = \max(p_n, \underset{1 \le i < n}{\max}{(r_i + r_{n-i})}) \text{, if } n \ge 1$,

$i=n$을 포함 시키고, $r_i$부분을 $ p_i$로 바꾸고, $ p_n +r_0 = p_n$으로 하면, 수식 간략화가 가능하다. \(\begin{aligned} r_n &= \begin{cases} \underset{1 \le i \le n}{\max}(p_i + r_{n-i}) & \text{if } n \ge 1 \\ 0 & \text{if } n = 0\\ \end{cases} \end{aligned}\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

# topdown with memo
lookup(p, n, r)
	# 저장되어 있다면 저장된 값 return 
	if r[n] >= 0 
    	return r[n]
    # base case 
	if n == 0
    	return 0
    q = -INF
    for i = 1 to n 
    	q = max(q, p[i] + lookup(p, n-i, r))
    # memo
    r[n] = q
    return q 

rodcut(p, n)
	let r[0..n] be a new array 
    # initialization
    for i = 0 to n 
    	r[i] = -INF
    return lookup(p, n, r)

# bottom up 
rodcut(p, n)
	let r[0..n] be a new array 
    r[0] = 0
    for j = 1 to n 
    	q = -INF
        # lookup with memo 
        for i = 1 to j
        	q = max(q, p[i] + r[j-i])
        r[j] = q 
    return r[n]

entry 갯수 $n$, 각 entry 계산하는데 $O(n)$ 걸린다. 따라서, $T(n) = O(n^2)$

c++

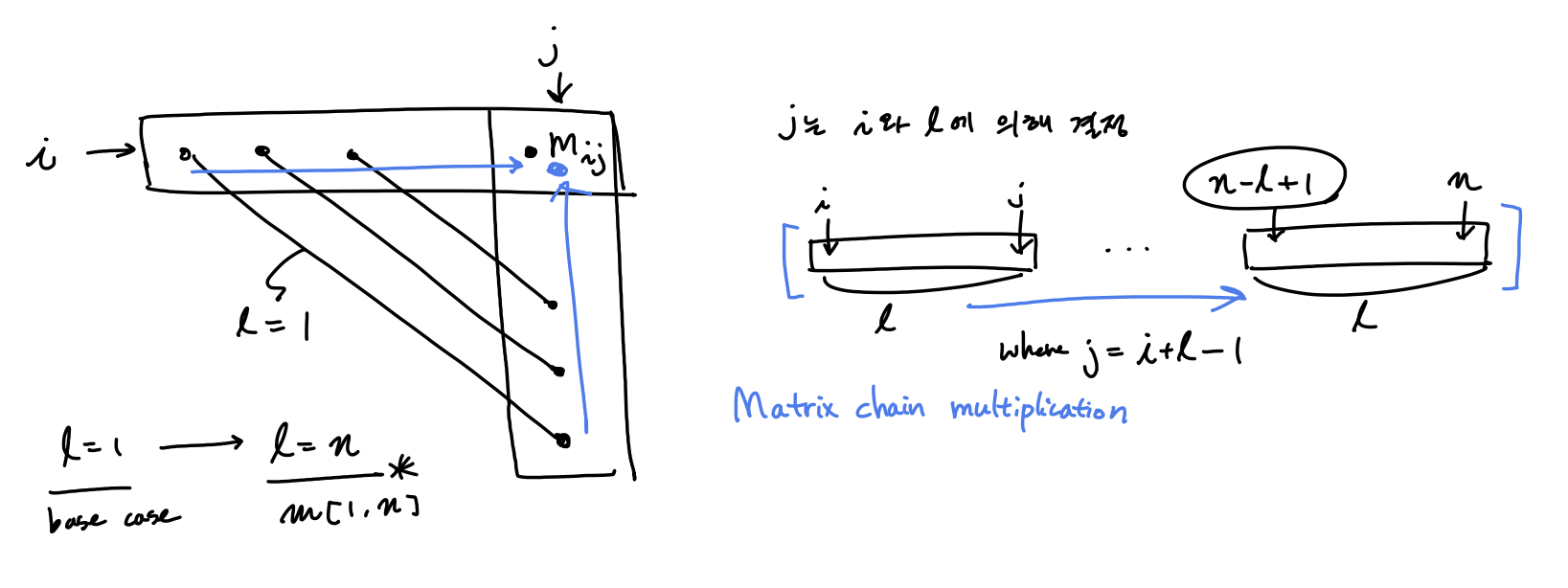
Matrix-chain multiplication

matrix multiplication 할때, 계산을 효율적으로 하기위해 parenthesization 을 어떻게 효율적으로 할 것인가? $m[i, j]$ 는 matrix chain multiplication $A_i A_{i+1} ..A_j $을 계산하는데 필요한 cost

$A_i \in \mathbb{R}^{p_{i-1} \times p_i}$ \(m[i,j] = \begin{cases} 0 & \text{if }i=j \\ \underset{i \le k <j}{\min}{(m[i,k] + m[k+1,j] + p_{i-1}p_kp_j)} & \text{if } i<j\\ \end{cases}\) $( A_i A_{i+1} ..A_k )$$( A_{k+1} A_{k+2} ..A_j )$ 에 대한 cost $m[i,k] + m[k+1,j] + p_{i-1}p_kp_j$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

# topdown with memo
lookup(p, m, i, j)
	# 저장되어있다면 저장된 값 사용
	if m[i,j] < INF
    	return m[i,j]
    # base case
    if i == j
    	return 0
    
    q = INF
	for k= i to j-1
    	q = min(q, lookup(p, m, i, k) + lookup(p, m, k+1, j) + p[i-1]*p[k]*p[j])
    m[i,j] = q
    return q 

MatrixChain(p, n)
	let m[1..n, 1..n] be a new n × n array 
    all m[:,:] be initialized by INF
    return lookup(p, m, 1, n)

# bottom up 
MatrixChain(p) # p = [p[0], ..., p[n]]
	n = |p|-1
    # base case (chain length l = 1 일때)
    for i = 1 to n 
        m[i,i] = 0
    for l = 2 to n 
    	for i = 1 to n-l+1
        	j = i+l-1
            m[i,j] = INF
            for k = i to j-1
            	q = min(q, m[i, k] + m[k+1, j] + p[i-1]*p[k]*p[j])
            m[i,j] = q
    return m[1,n]

bottom up 방식이 좀 어려울수 있다.

chain length $l = 1, …, n$ 까지 minimum cost를 업데이트 하면 optimal cost를 찾을 수 있다.

matrixchain

$T(n) = O(n^3)$

c++

Longest Common Subsequence

$C_{i,j}$ 는 $X_i$ 와 $Y_j$의 LCS 길이 $X_i = <x_1, …, x_i>, Y_j = <y_1, …, y_j>$ \(C_{i,j} = \begin{cases} 0, &\mbox{if } i = 0 \or j = 0 \\ C_{i-1,j-1} + 1 &\mbox{if } i,j > 0 \and x_i = y_j \\ \max\{C_{i-1,j}, C_{i, j-1}\} &\mbox{if } i,j > 0 \and x_i \neq y_j \end{cases}\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

# topdown with memo
lookup(X, Y, c, i, j)
	if c[i,j] >= 0
    	return c[i,j]
    # base case
    if i==0 or j==0
    	c[i,j] = 0
    	return c[i,j]
    
    # i > 0 or j > 0
    if X[i] == Y[j]
    	c[i,j] = lookup(X, Y, c, i-1, j-1) + 1
        return c[i,j]
    else
    	c[i,j] = max(lookup(X, Y, c, i-1, j), lookup(X, Y, c, i, j-1))
        return c[i,j]
    
LCS(X, Y)
	m = |X|
	n = |Y|
	let c[0..m, 0..n] be a new array 
    # initialization
    all c[:,:] be initialized by -INF
    return lookup(X, Y, c, m, n)
    
    
    
# bottom up 
LCS(X, Y)
	m = |X|
    n = |Y|
    let c[0..m, 0..n] be a new array 
    all c[:,:] be initialized by -INF
    # base case
    if i == 0 to m
    	c[i,0] = 0
    if j == 0 to m
    	c[0,j] = 0
    for i = 1 to m 
    	for j = 1 to n 
        	if X[i] == Y[j]
            	c[i,j] = c[i-1, j-1] + 1
            else 
            	c[i,j] = max(c[i-1, j], c[i, j-1])
    return c[m,n]

$T(n) = O(mn)$

c++

Assembly Line

pdf 참조

c++

0 - 1 knapsack

0-1 Knapsack problem is not satisfied with Greedy choice property

$i$ 는 item index, $w$ 는 possible weight, $v_i$는 item $i$ 의 가격

$c[i,w]$ 는 item $i$개를 주머니에 넣고, 주머니에 담을수 있는 weight가 $w$ 일때의 주머니 안의 물건들 가격
\(c[i,w] = \begin{cases} 0 &\text{if }i=0 ~ \or w=0 \\ c[i-1,w] &\text{if } i > 0 ~ \and w < w_i \\ max(v_i + c[i-1,w-w_i], c[i-1,w]) &\text{if } i > 0 ~ \and w \ge w_i \end{cases}\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

# topdown with memo
# V[i], W[i]는 item i에 대한 pric와 weight 정보 array
# W(array)와 w(scalar)는 다르다.
lookup(V, W, c, i, w)
	if c[i,w] >= 0
    	return c[i,w]
    # base case
    if i==0 || w==0
    	c[i,w] = 0
        return 0
    if W[i] > w 
    	c[i,w] = lookup(V, W, c, i-1, w)
        return c[i,w]
    else
    	c[i,w] = max(V[i] + c[i-1, w-W[i]], c[i-1, w])
		return c[i,w]

knapsack(V, W, maxW)
	n = |V|
	let c[0..n, 0..maxW] be a new array
    all c[..] initialized by -INF
    return lookup(V, W, c, n, maxW)
        
# bottom up
knapsack(V, W, maxW)
    n = |V|
	let c[0..n, 0..maxW] be a new array
    all c[..] initialized by -INF
    for i = 0 to n
    	for w = 0 to maxW
        	if i==0 || w==0
            	# base case 
            	c[i,w] = 0
            else
				if W[i] > w
                	c[i,w] = c[i-1, w]
                else
                	c[i,w] = max(V[i] + c[i-1, w-W[i]], c[i-1, w])
    return c[n, maxW]

$T(n) = O(nW_{max})$

c++

Greedy

python

Activity Selection Problem

여러 starting time, finish time 을가진 activity $a = [s,f]$들이 있을 때 주어진 시간내에 compatible 한 activity들을 가장 많이 포함시킬 수 있도록 scheduling 하는 문제

naive 하게 생각 해보면 $n$개의 activity들 이 있을때 $2^n$ 가지의 모든 subset 에서 각 subset 마다 가지고있는 activity들이 서로 compatible한지 검사하고, 모든 activity들이 compatible하다면 그 갯수를 저장하고, 그 중 최대를 갖는 subset를 찾는다.

$S_k _{k=[1,2^n]} = { \text{최대 n 개의 activity} }$

이때, ${ .. }$안의 각 activity들이 서로 compatible 한가 test (All pair로 검사한다면, $O(n^2)$걸림 )

따라서, $O(2^n n^2)$ 이므로 너무 비싸다.

조금 나아가 생각해보면, activity 들이 만약 finishing time에 의해 sorting 되어 있다고 가정해보자.

그러면 compatible test 에서 linear하게 scan하면 된다. ($i$번째에서 starting time이 $i-1$번째의 finishing time보다 앞선 다면 compatible하지 않은 것이므로 즉, $a_i.s < a_{i-1}.f$ 이면 non compatible 함)

따라서, $O(2^n n)$ 으로 약간 개선된다. (activity 들이 만약 finishing time에 의해 sorting 되어 있다고 가정한 상황이므로 sorting 시간 무시)

DP 이용

여기서 더 개선 하기 위해선, 모든 subset을 보지 않고, overlapping되는 subproblem들을 이용한다.

(새롭게 notation을 정의함)

가정 상황: activity 들이 finishing time에 의해 sorting 되어 있다.

여기선 어떻게 문제를 정의 하느냐에따라 time complexity가 달라질 수 있다.

**approach1 **교재의 방식은

act1

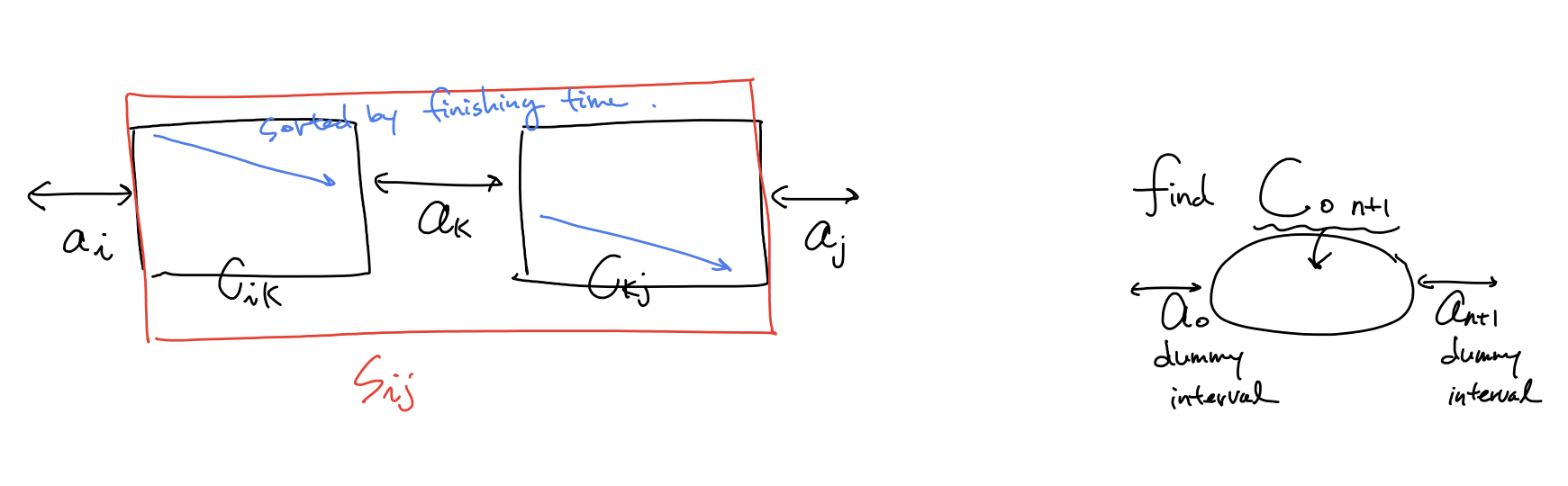
$S_{0,n+1}$ 의 원소 갯수가 최대가 되도록 선택을 하고 싶다! (dummy 원소 $a_0, a_{n+1}$ 두고)

$c[i,j]$를 $S_{ij}$ 안에서 compatible한 activity들의 최대수로 정의 \(c[i,j] = \begin{cases} 0 & \text{if}~ S_{ij} = \empty \\ \underset{i < k < j ~ s.t. ~ a_k ∈ S_{ij}}{\max}(c[i,k] + c[k,j] + 1) & \text{if}~ S_{ij} \neq \empty \end{cases}\) $T(n) = O(n^3) $

approach2 또 다른 방식으로 entry수를 $n$으로 줄여 보았다.

act2

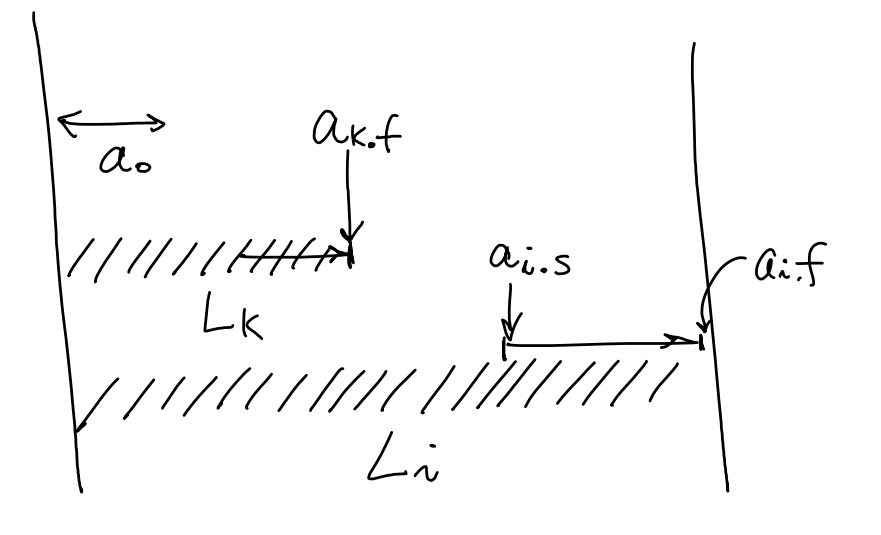
$L_i$ 는 $a_i$를 포함 하는 $0,…, i $에 대해 compatible 한 activity 갯수

따라서, $L[0..n]$까지 업데이트 후에 가장 max인 값을 택해야한다. $$ \begin{aligned} L_i &= \begin{cases} \underset{0 \le k<i ~ s.t ~ a_k.f \le a_i.s}{\max}{(L_k + 1)} & \text{if } a_0.f \le a_i.s &\text{#하나라도 compatible 한 activity존재}
1 & \text{o.w} \end{cases}
result &= \underset{1 \le i \le n}{\max}{L_i}

\end{aligned} $$ $T(n) = O(n^2) $

c++

greedy choice이용

greedy choice는 compatible한 activity중 finishing time이 가장 빠른것을 선택.

redefine for greedy algorithm

$S_{ij} -> S_k $ = {$a_i ∈ S: s_i \ge f_k $}

If we use greedy algorithm, DP formula can be transformed.

\[\begin{aligned} c[0,n+1] &= c[0,m_1] + c[m_1, n+1] + 1 &m_1\text{ is greedy choice} \\ &= c[m_2, n+1] + 1 + 1 &m_2\text{ is greedy choice}\\ &= c[m_3, n+1] + 1 + 1 + 1 &m_3\text{ is greedy choice}\\ &= ~ ... \\ &= c[m_m, n+1] + m \end{aligned}\]

note that $c[0,m] = 0, c[m_1,m_2] = 0, … ,c[m_{m-1},c_m] = 0$ , where $m \le n $

따라서, entry를 줄일 수 있다(entries are decreased by O(n), each entry takes O(1)).

greedy algorithm에 대한 recursive formula 를 적어보았다. $$ \begin{aligned} m_k &= \begin{cases} 0 & \text{if } k=0 &\text{ base case}
k & \text{if } a_{m_{k-1}.f} \le a_k.s &\text{find a first compatible activitiy}
m_{k-1} & \text{o.w } \end{cases} \

A_k &= \begin{cases} A_{k-1} + 1 & \text{if } a_{m_{k-1}}.f \le a_k.s &# k\text{ is greedy choice}
A_{k-1} \end{cases} \end{aligned}
$$ $A_n$ 값을 찾으면 된다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# recursive version 
def Recursive_Greedy(s,f,k,n)
    m = k+1
    # Find appropriate m for using optimal sol
    # m은 compatible한 activity중  finishing time이 가장 빠른 activity index 
    while m <= n and s[m] < f[k]
        m = m + 1 
    
    if m <= n 
        return 'a_m' union Recursive_Greedy(s,f,m,n)
    else:
        return None
        
# iterative version 
def Iterative_Greedy(s,f)
    n = |s|
    A = 'a_1' # A always has a1 
    k = 1 
    for m = 2 to n:
        if s[m] >= f[k]:
            A = A union 'a_{}'.format(m)
            k = m 
    return A

Therefore, \(T(n) = O(n), \text{ suppose that prepressing sortng }~ a_k \text{ with finishing time }\) c++

Fractional Knapsack

Fractional Knapsack Problem through Greedy algorithm

Greedy choice : first of all, an item with higher Unit price per weight must be selected

preprocessing으로 quick sort를 이용하여 무게당 가격이 높은 순으로 $O(nlogn)$시간에 sorting하고,

그 순서대로 아이템을 $O(n) $시간에 linear scan하며 물건을 담을 수있다면 물건을 담고, 아니면 일부만 담는다.

notation은 0-1 knapsack problem 과 동일

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# assume that V[i], W[i] sort by decreasing order with (V[i]/W[i])
knapsack(V, W, maxW) {
    n = |V|
	residualw = maxW;
    profit = 0
	for i = 1 to n
    	# 담을 수 있다면, 담는다.
		if W[i] <= residualw
			profit = profit + V[i]
			residualw = residualw - W[i]
		# 담을 수 없다면, 일부만 담고 종료
    	else {
			# w[i] > residualw
			profit += V[i]*(residualw/w[i]);
			break;
		}
	}
	return result;

c++

Graph

Implementation Pros and Cons

Describe the linked list representation of a graph

각 정점에 인접한 정점들을 2차원 배열의 자료구조로 표현하는 방법이다.

정점의 개수가 n개인 그래프가 주어졌을 때 n$\times$ n matrix를 준비한다.

가중치가 없는 그래프라면 가중치의 값을 항상 1로 할당한다.

정점 i에서 정점 j로 가는 간선이 존재하면 그 가중치의 값을 원소의 값으로 할당한다.

간선이 존재하지 않으면 값을 0으로 할당한다.

  • Advantage
    • 간선의 존재여부를 확인하는데 상수 시간 (O(1))이 소요된다.
  • Disadvantage
    • 그래프를 생성하는데 $n^2$ 의 메모리와 O($n^2$) 의 시간이 소요된다.

Describe the adjacency matrix representation of a graph

각 정점에 인접한 정점들을 리스트로 표현하는 방법이다.

정점의 개수가 n개인 그래프에서 n 길이의 list를 준비한다.

각 정점에 인접한 정점들을 연결리스트로 매단다.

각 노드는 정점번호, 가중치, 다음 정점의 포인터 로 구성된다.

필요한 총 노드 수는 총 간선수의 두배이다.

  • Advantage
    • 그래프를 생성하는데 2 E 만큼의 메모리가 소요되므로 간선 수가 적은 경우 유용하다.
  • Disadvantage
    • 간선 수가 많은 경우 ( E > V ) 오히려 필요한 오버헤드가 크다.
    • 간선의 존재여부를 확인 하는데 O(n) 시간이 소요된다.

BFS

Queue를 이용하여 search 혹은 shortest path 찾음

가장 쉬운 알고리즘으로는 모든 edge weight(distance)를 1로 둔 방식

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

BFS(G, s)
	let visited[1 ..|G.V|] be a boolean array and all initialized by False
	create queue Q
	Q.push(s)
	visited[s] = True

	while !Q.empty()
		u ← Q.pop()
        
		# update u.d timing
        # print u
        
		for v in G.adj[u]
        	# 이전에 방문한적이 없다면 방문
			if visited[v] == False
				Q.push(v)
				visited[v] = True

# for forest G 
BFSAll(G)
	let visited[1 ..|G.V|] be a boolean array and all initialized by False
    for s in G.V
    	if visited[s] == False
            # 기존 BFS에 visited를 argument로 import하여 사용
        	BFS(G, s, visited)
adjacent list 자료구조를 사용한 graph라면 모두 한번씩 보게 되므로 $T(n) = O( V + E )$

blog 설명 python c++

DFS

stack을 이용하여 search 혹은 shortest path 찾음

DFS can be implemented by recursive call without stack

because recursive call means using a stack in our main memory(stack field)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

# iterative version
DFS(G, s)
	let visited[1 ..|G.V|] be a boolean array and all initialized by False
	create stack S
	S.push(s)
	visited[s] = True

	while !S.empty()
		u ← S.pop()
        
		# update u.d timing
        # print u
        visited[u] = True
        
		for v in G.adj[u]
        	# 이전에 방문한적이 없다면 방문
			if visited[v] == False
				S.push(v)
                
# recursive version
# function call시 내재된 stack이용 
Util(G, u, visited)
	# similar with u ← S.pop() 
    
	# update u.d timing
    # print u
	visited[u] = True;
    
    for v in G.adj[u]
    	if visited[v] == False
        	Util(G, v, visited)
    
    # update v.f set timing
    # ..
    return 

DFS(G, s)
	let visited[1 ..|G.V|] be a boolean array and all initialized by False
    # similar with S.push(s)
    Util(G, s, visited)

# for forest G 
DFSAll(G)
	let visited[1 ..|G.V|] be a boolean array and all initialized by False
    for s in G.V
        if visited[s] == False
        	# same with Until(G, s, visited)
        	DFS(G, s, visited)
adjacent list 자료구조를 사용한 graph라면 모두 한번씩 보게 되므로 $T(n) = O( V + E )$

blog 설명 python c++

Topological Sort

DFS 를 쓰는 application 중 한가지인 Topological sort 방법

기본 가정: DAG(Directed Acyclic graph)에서만 쓸수 있다.

DAG에서 즉, 방향 그래프에 존재하는 각 정점들의 선행 순서를 위배하지 않으면서 모든 정점을 나열하는 것

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

topoDFS(G, u, visited, S)
	visited[u] = True
    for v in G.adj[u]
    	if visited[v] == False
        	topoDFS(G, S, visited, v)
            
	# update v.f set timing
    S.push(v)
    
TopoSort(G)
    create stack S
    create list L
    let visited[1 ..|G.V|] be a boolean array and all initialized by False;

    # DFS를 하면서 finishing time의 increasing order로 Stack S 에 넣는다.
    # adjacent list 에서의 순서에 따라 search 순서가 다를 수 있으므로 생각할때는 다음과 같이 가정
    # Let assume that the node with small number has a higher priority when DFS search  
    for u in G.V
        if (visited[u] == false)
            # DFS search starts at 'u' ...
            topoDFS(G, u, visited, S)
    
    # Stack S를 뒤집은 결과를 L이라하면, 이 결과가 곧 topolgical sort 
    while !S.empty()
        L ← S.pop()

    return L
adjacent list 자료구조를 사용한 DFS 를 이용했으므로 $T(n) = O( V + E )$

c++ python greeksforgeeks 설명 한국어 블로그

Single Shortest Path

source vertex 로부터의 shortest path 와 distance를 찾아 내는 알고리즘

Bellman Ford

기본가정: no negative weight cycle(있다면 False return)

Dijkstra’s algorithm과 달리 Bellman Ford 알고리즘은 가중치가 음수인 경우에도 적용 가능. 음수 가중치가 사이클(cycle)을 이루고 있는 경우에는 작동하지 않는다.

naive 하게 그래프 정점 수만큼 그래프 내 모든 엣지에 대해 edge relaxation을 수행한다. 그러면 (negative weight cycle 이 없다는 가정하에) 모든 정점수 만큼의 relaxation을 돌았을때, shortest path를 찾을 수 있다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

Bellman(G, s)
	# shortest distance 값을 저장할 array
	let d[1 ..|G.V|] be a new array
    
    # initialization
    d[k] = INF for all k in G.V except for k == s 
    d[s] = 0
    
    # edge relaxations for all cases O(VE)
    for i = 1 to |G.V|
    	for (u,v) in G.E
        	if d[v] > d[u] + w(u,v)
            	d[v] = d[u] + w(u,v)
    
    # check whether eixist negative weight cycle
    # negative edge 가 있다면 edge relaxation을 했을때
    # shortest path distance보다 작은 distance 가 존재 할 것이다.
    for (u,v) in G.E
    	if d[v] > d[u] + w(u,v)
        	return False
        
    return d

모든 cases 에 대해 edge relaxation을 수행해야하므로 $T(n) =O(VE)$

c++ python 한국어 블로그

DAG

Topological sort를 사용하여 Bellman Ford 를 좀더 개선한 방식

기본가정: Topological sort를 사용해야하므로 DAG에 대해서만 사용가능

Bellman ford 알고리즘은 naive하게 모든 가능한 경우의 수에 대해서 edge relaxation 을 수행하였다.

DAG algorithm은 좀더 효율적이게 topolgical sort를 한 순서의 정점 리스트를 바탕으로 edge relaxation을 수행

1
2
3
4
5
6
7
8
9
10
11
12
13
14

Bellman(g, s)
	let d[1 ..|G.V|] be a new array
	# initialization
    d[k] = INF for all k in G.V except for k == s 
    d[s] = 0
    
    # edge relaxations for a efficient way 
    L = TopoSort(G);
    for u in L
    	for (u,v) in G.E
        	if d[v] > d[u] + w(u,v)
            	d[v] = d[u] + w(u,v)
                
    return d

Topological sort를 한 List 순으로 진행되므로 $T(n) =O(V + E)$

c++ python

Dijkstra

기본가정: 모든 edge가 non negative 이어야함 (가중치가 음수인 경우 작동하지 않는다)

priority queue 를 이용한 알고리즘

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

# version 1 
Dijkstra(G, s)
	# initialization
    k.d = INF for all k in G.V except for k == s 
    s.d = 0
     
    # vertices in set S have already shortest path distance
    create set S 
    # priority queue Q(min heap)의 {key=vertex, value=vertex.d]}
    # value가 낮을 수록 priority is higher 
    create priority queue Q
    Q ← all G.V 
    
    while !Q.empty()
    	u = Q.pop()
        S ← u
       	for v in G.adj[u]
        	if v not in S and v.d > u.d + w(u,v)
            	v.d = u.d + w(u,v)
                # update distance of v in O(log|V|)
                Q.update_value(v, v.d) 

# version 2 (priority queue에 update_value 함수가 없는 경우)
# 대신, 느림
Dijkstra(G, s)
    let d[1 ..|G.V|] be a new array
    # initialization
    d[k] = INF for all k in G.V except for k == s 
    d[s] = 0

    # vertices in set S have already shortest path distance
    create set S 
    # priority queue Q(min heap)의 {key=vertex, value=d[vertex]}
    create priority queue Q
    Q ← {s, d[s]}

    while !Q.empty()
        u = Q.pop()
        S ← u
        for v in G.adj[u]
            if v not in S and d[v] > d[u] + w(u,v)
                d[v] = d[u] + w(u,v)
                # push updated {v, v.d} in Q
                Q.push(v, v.d)
version 1 의 time complexity 로 설명하면, $O(( V + E )log V )$

geeksforfeeks c++ python python hw

Dijkstra algorithm correctness 증명

proof by Induction 을 통해 증명하겠다.

loop invariant 는 매 iteration의 시작점에서 $u.d = \delta(s,u)$ 즉, shortest path distance

shortest path 가 결정된 vertex 집합을 $S$라 하고, 매 iteration 마다 정점 하나씩 추가된다.

base case: 시작점 source vertex의 shortest distance 는 0이므로 $s.d = \delta(s,s) = 0$ correct

dijkstra

Induction step: 임의의 iteration 이전까지는 S안에 shortest path distance들이 결정된 vertex들만 들어가다가 dijkstra 알고리즘에의해 처음으로 $\color{red}u.d \neq \delta(s.u)$ 인 $\color{red}u$가 queue에서 뽑혔다고 하자.(모순을 이끌어내겠다.)

이때, $s$부터 $u$ 까지의 shortest path에서 $S$의 경계점 바로 직전과 직후의 정점 $x$와 $y$ 를 생각해 보자.

일단. $x.d = \delta(s,x)$ 가 자명하다($S$가 shortest path distance가 결정된 정점 집합이라고 했으므로)

그래서, $y.d = \delta(s,x) + w(x,y) = \delta(s,y)$ 는 shortest distance 인 상황이며,

이 사실과 negative edge가 없다는 사실로부터 ($\delta(y,u) \ge 0$) \(\begin{aligned} u.d &> \delta(s,u) = y.d + \delta(y,u)\ge y.d \\ \therefore u.d &> y.d \end{aligned}\) 임을 주목해보자.

이 상황에서, 우리의 처음 가정이 맞다면, $u.d \le y.d $이어야한다. ( dijkstra 알고리즘에의해 처음으로 $u.d \neq \delta(s.u)$ 인 u가 queue에서 뽑혔다고 했으므로 $u.d$가 같거나 더 작아야한다.)

하지만, 그렇지 않기 때문에 모순이 된다.

따라서, $\color{red}u.d = \delta(s,u)$ 인 $\color{red}u$가 뽑혀야만 한다.

web 영문 설명

All pair shortest path

Naive DP

$ l_{ij}^{(m)}$ node $i$ 부터 node $j$ 까지 가는데 최대 $m$ 개의 edge를 거쳐서 가는 path의 minimum weight

[intution]

이때, 총 노드의수 를 $n$ 이라하면, 거쳐가는 edge의 수 $m$이 $n-1$보다 많으면 반복되는 node가 존재한다는 뜻이므로 cycle이 있다는 뜻인데, negative edge가 없다고 가정했으므로 당연히 cycle을 돌면 shortest path의 wieght sum 보다 높은 path sum이 된다. 즉, $m = n - 1$ 까지 update하면 optimal solution이 됨

$ {min}{(l_{ij}^{(m-1)}, \underset{1 \le k \le n}{min}{(l_{ik}^{(m-1)} + w_{kj} )} )} = \underset{1 \le k \le n}{min}{(l_{ik}^{(m-1)} + w_{kj} )} ~~~~ \text{if } m \ge 1$

$\because k = j $ 이면 $w_{jj}=0$ 이 되므로 case가 합쳐질수 있다.

따라서, recursive formula 는 다음과 같다.
\(l_{ij}^{(m)} = \begin{cases} \underset{1 \le k \le n}{min}{(l_{ik}^{(m-1)} + w_{kj})} & \text{if } m \ge 1 \\ l_{ij}^{(0) } = \begin{cases} 0 & \text{if } i = j\\ \infty & \text{if } i \neq j \end{cases} & \text{if } m = 0 \\ \end{cases}\)

여기서 또 주목할 만한점은 $m=1 $ 일때는 $l_{ij}^{(1)} = w_{ij}$ 이므로 $l_{ij}^{(0)}$을 굳이 계산할 필요는 없다.

$O(n^4)$ 이 걸리는 아주 비싼 알고리즘이다. $ \because n^3$ entries, each entry takes $O(n)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# update next step for m 
update(L,W)
	n = len(L)
	let L`[1..n, 1..n] be a new array
	for i = 1 to n 
		for j = 1 to n 
			L`[i,j] = INF
			# each entry can be calculated in O(n)
            for k = 1 to n 
            	L`[i,j] = min(L`[i.j], L[i.j] + W[k,j])
    return L`

# given a graph's weight matrix W[1..n, 1..n]
APSP(W)
	n = len(W)
	let L[1..n, 1..n] be a  new array
	
	# initialization
	L = W
	
	# update L for m 
	for m = 2 to n-1
		L =  update(L, W)
    
    retrun L

python

$m$ 에 대해 linear 하게 update 하는 위의 방식을 조금 더 개선해보자.

L 의 계산이 associative한 성질을 가지며, $m \ge n - 1$이면 shortest path weight는 고정되어 L 은 바뀌지 않는다.

따라서, associative 하게 $k$번 계산하여 $2^k \ge n-1$ 일 경우 optimal sol으로 고정된다.

따라서, optimal sol에 도달하기 까지$k = O(logn)$ 번 연산하게 됨.
\(\begin{aligned} L^{(1)} &= W \\ L^{(2)} &= W^2 = WW \\ L^{(4)} &= W^4 = W^2W^2\\ ... \\ L^{(2^k)} &= W^{2^k} = W^kW^k\\ L^{(2^k \ge~ n-1)} &= W^{2^k \ge ~ n-1} (fixed)\\ \end{aligned}\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14

# given a graph's weight matrix W[1..n, 1..n]
faster_APSP(W)
	n = len(W)
	let L[1..n, 1..n] be a  new array
	
	# initialization
	L = W
	
	# update L for m 
	for m = 2 < n-1
		L =  update(L, L)
		m = m*2
    
    retrun L

$O(n^3logn)$ 으로 계선되었지만 여전히 비싼 알고리즘이다.

Floyd Warshall Algorithm

All pair shortest path with DP 를 조금더 효율적으로 해보자는 접근

기본 가정: no negative cycle

먼저 주어진 그래프에 대한 edge정보로 부터 matrix $C$ 정의 \(C_{ij} = \left \{ \begin{matrix} 0 & \text{if } i=j \\ c(i,j) \ge 0 & \text{if } i \ne j, (i,j) \in E \\ \infty & \text{if } i \ne j, (i,j) \notin E \\ \end{matrix}\right.\) $d_{ij}^{(k)}$: $v_i \text{~} v_j$ 까지 가는데 $v_1, .., v_k$를 거쳐가는지에 대한 유무가 update된 shortest path distance ($k$ 가 증가함에따라 점점 더 많은 노드정보를 거쳐가는것에 대한 정보를 업데이트 된다).

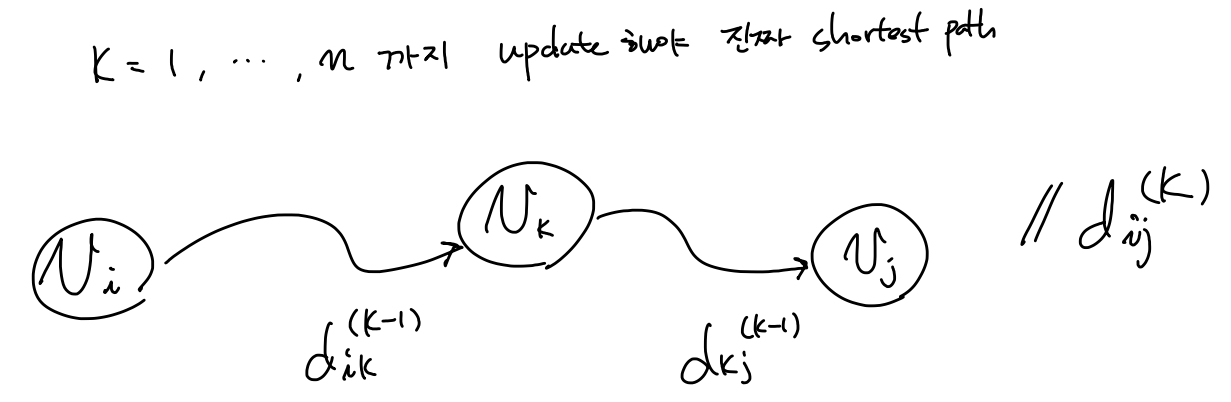그림 \(d_{ij}^{(k)} = \left \{ \begin{matrix} c(i,j) \ge 0 & \text{if } k=0 \\ min \{ d_{ij}^{(k-1)}, d_{ik}^{(k-1)} + d_{kj}^{(k-1)} \} & \text{if } k \ge 1 \\ \end{matrix} \right.\) Time complexity: $O(n^3)$ because all entry $(1\le i,j,k\le n)$ , is $n^3$, each entry takes $O(n)$ time

back propagation: $P^{(k)}$의 각 entry $P_{ij}^{(k)}$가 의미하는것은 현재까지 업데이트된 $v_k$ 를 지나는 $v_i \rightsquigarrow v_k \rightsquigarrow v_j$ 의 shortest path 정보를 의미한다. ($k = 1,..,n$ 까지 모두 update되어야 진짜 shortest path가 됨)

algorithm

python c++

Johnson

Dijkstra 와 BallmanFord를 이용한 알고리즘

c++ python

MST

MST(Minimum Spanning Tree) 를 구하는 것

기본 용어 설명

light edge: 어떤 정점 집합을 둘로 나누는 cut을 했을때, crossing edge 중에 weight가 가장 작은 edge

safe 하다: weight의 sum 이 minimum을 갖는 spanning tree에 대해서 어떤 edge $(u,v)$ 를 더해도 그 특성이 유지 된다면 safe 하다고 한다.

일반적인 MST 알고리즘은 다음과 같다

1
2
3
4
5
6

MST(G)
	create set A 
	while A does not form a spanning tree
		find an edge (u,v) that is safe for A 
		A = A union {(u,v)}
    return A

Kruskal

greedy method 을 이용하여 네트워크(가중치를 간선에 할당한 undirected 그래프)의 모든 정점을 최소 비용(최소 경로)으로 연결하는 최적 해답을 구하는 것

disjoint set 자료구조를 활용하며, greedy 하게 light edge 를 추가하면 safe함을 이용함

방법: disjoint set 자료구조를 활용하여 independent 한 tree들을 만들고, 작은 weight를 가진 edge 순서대로 crossing하는 edge에 대해서 tree들을 merge해 나간다. 즉, safe 할때, merge한다.

disjoint set에 2 가지 heuritic 이 사용된다.

  1. path compression
  2. union by rank

이 2가지의 heuristic을 사용하면, n 개의 disjoint set이 있을때(n 번의 makeset operation 이 수행된 상태),

makeset, findset,union operation이 모두 m 번 call 된다고하면,

전체 operation을 수행하는데 $O(m\alpha(n))$만큼의 시간이 걸린다.

여기서, $\alpha(n)$ 은 $logn$ 에 upper bounded 되어있어서 효율적인 operation 수행이 된다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

DisjointSet
	__init__(n)
    	let parent[1..n] be a new array
        let rank[1..n] be a new array
        # DisjointSet을 만드는 순간 n 번의 makeset operation 
    	for i=1 to n 
        	rank[i] = 0
            parent[i] = i 
    
    findset(u)
    	# path compression(한번 representative를 찾을때 이어놓는다)
    	if u != parent[u]
        	parent[u] = findset(parent[u])
        retun parent[u]
	
    union(x, y)
    	# find each representative for the set that includes x and y
    	x = findset(x)
        y = findset(y)
        
        # union by rank(rank가 작은 disjoint set을 큰쪽에 연결)
        # y 의 rank 가 x 보다 같거나 크면, y를 x.p 로 한다. 
        # (rank가 같을때는 y에 연결후, y rank만 1증가) 
        if rank[x] > rank[y]
        	parent[y] = x 
        else 
        	parent[x] = y
        if rank[x] == rank[y]
        	rank[y] = rank[y] + 1

kruskal(G)
	# weight sum 
    sum = 0;
    
    # initialization
    create DisjointSet Ds;
    # makeset for all v in G.V : O(V)
    Ds ← all v in G.V 
    create a empty MST set A 
    
    # preprocessing
    # sort G.E by (weight)increasing order : O(ElogE) 
    sort(G.E);  
    
    # 서로 다른 distinct component를 crossing하는 edge 중에서 
    # weight가 가장 작은 light edge를 greedy 하게 찾는과정(DisjointSet 이용)
    # O((V+E)α(V)) 여기서 α(V) upper bounded by O(logV)
    for (u,v) in G.E
        if Ds.findset(u) != Ds.findset(v) 
            # (u,v) edge is a greedy choice 
            # update the sum of MST weight 
            sum = sum + w(u,v);
            Ds.union(u, v);
            A = A union {(u,v)}

    return sum;
kruskcal 알고리즘이 전체과정에서 makeset $O( V )$, findset $O( E )$, union $O( V )$ 번 call 되므로
kruskcal 알고리즘에서 for문에서 쓰인 disjoint set의 operation 수는 $ V + E $ 번이므로
time complexity는 $O(( V + E )\alpha( V )$ 인데,

$\alpha(n)$ 은 $logn$ 에 upper bounded 되어 있고,

graph G가 connected 되어있다면, $ E \ge V -1 $ 이고,

graph G가 sparse 하다면 $|E| > |V|^2$ 이므로,
\(\begin{aligned} T(n) &= O((V|+|E|)\alpha(|V|)) \\ &\le O(|E|\alpha(|V|)) \\ &\le O(|E|log|V|) \\ &\le O(|E|log|E|) \\ &\le O(|E|log|V|^2) = O(|E|log|V|) \end{aligned}\)

c++ python

Prim

root note $r$ 을 주면 undirected graph $G$에서 priority queue를 이용하여 모든 vertex중에서 근접한 edge의 weight를 업데이트 해나가면서 light edge 를 찾아 MST를 찾는다. 즉, safe한 edge를 더해나간다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

prim(G, r)
    # MST에서 predecessor vertex를 저장하고, 업데이트 할 array
    let parent[1..|G.V|] be a new array 
    
    # initialization
    u.d = INF for all u in G.V except for k == r 
    r.d = 0
    parent[u] = Nan for all u in G.V 
    
    # priority queue Q(min heap by value)의 {key=vertex, value=vertex.d}
    create priority queue Q 
    Q ← all G.V 
    
    while !Q.empty()
    	u = Q.pop()
       	for v in G.adj[u]
        	# light edge가 발견되면 v의 value를 update하고, Q에도 반영
        	if v in Q and w(u,v) < v.d
            	v.d = w(u,v)
                parent[v] = u
                # update distance of v in O(log|V|)
                Q.update_value(v, v.d)

light edge를 발견하면 Q 에서 나오고 더이상 parent와 d 가 업데이트 되지 않고, 그에 해당하는 edge가 MST가 됨을 주목하자!

따라서, Q에서 모든 vertex를 꺼내면 MST가 찾아지는데

이 알고리즘에 binary heap을 사용했을때, Q.pop()이나 Q.update_value() 연산이 $logV$ 만큼 걸림을 우린 알고있다.

그래서 알고리즘 내부의 수행 시간을 생각해보면,

1
2
3
4
5
6
7
8
9

# O(VlogV)
while !Q.empty()
	u = Q.pop()
	
# adjacent list를 썻다면 O(ElogV) 
# 왜냐하면 모든 edge를 돌게 되고, update_vale가 O(logV) 
while !Q.empty()
 	u = Q.pop()
	for v in G.adj[u]
따라서, $T(n) = O((V+E)logV) = O(ElogV)$ $\because $ graph G가 connected1 되어있다면, $ E \ge V -1 $ 이므로

wiki python hw

Prim algorithm correctness 증명

proof by induction, or mathmatical induction을 이용 하여 증명하겠다!

loop invariant 는 매 iteration의 시작점에서의 tree 는 MST 의 subtree

base case: 처음 시작할때 tree는 아무 노드도 없으니까 당연 optimal

induction step: k번째로 edge를 추가하려는 상황 지금까지의 알고리즘에 의한 tree는 optimal이라 가정

$T^{(k)}$는 MST $T^*$의 subgraph 인 상황

알고리즘 동작대로 해보고 다음 iteration 시작하기전 $T^{(k+1)}$ 역시 $T^* $의 subgraph인지 확인하겠다.

만약 알고리즘에 의해 어떤 edge $e = (u,v)$ 를 추가하는데 $e$가 $T^* $의 edge가 아니라고 가정! (모순을 찾겠다)

일단, $T^* \cup e$ 는 사이클이 반드시 생긴다. ($T^*$는 minimums panning tree2인데 edge를 추가했으니까 )

MST

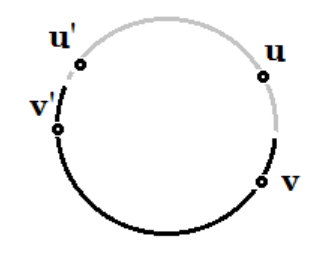
이 사이클 안에서 $u’$은 $T^{(k)}$ 안에 있고, $v’$ 은 $T^{(k)}$ 밖에 있는 $e$와 다른 어떤 한 edge $e’=(u’,v’)$ 을 고르자

(회색선은 $T^{(k)}$ 의미)

그때 prim 알고리즘에서는 weight가 작은 edge를 선택하므로 $e$를 선택 했다면 $ w(e) \le w(e’)$ 인 상황이다.

$T ‘ = T^* - e’ + e$ 라고하면,

$ T’ \le T^* $ 가 되므로 $T^* $는 optimal 이 아닌 모순적 상황이다.

따라서, 매 iteration 마다 prim 알고리즘에 의해 추가되는 $e$는 MST $T^*$ 에 포함된 edge이다.

한글 blog 증명

Flow Maximization

flow network (2018_2 APM hw3 참조)

(1) flow network definition: 그래프에는 src, sink node가 있고, edge가 있으면 nonnegative capacity 를 갖고, edge가 없으면 capacity가 0 이됨.

flow definition: capacity $c$ , src, sink 노드 $s, t$ 를가진 flow network $G = (V,E)$ 에 대해서 edge $E$ 를 어떤 실수값 $ \R $ 로 mapping 시켜주는 함수 인데, 2가지 성질을 갖는다.

  1. Capacity constraint: $ 0 \le f(u,v) \le c(u,v) $ ,$\forall (u,v) \in E $

    flow 값이 제한됨

  2. Flow conservation: $\sum_{(u,v)\in E}{f(u,v)} = \sum_{(v,w)\in E}{f(v,w)} $ ,$\forall v \in V - {s,t} $

    src, sink 를 제외한 노드 $v$에 들어온 flow 양과 나가는 flow 양이 같다.

**(2) flow maximization problem definition: **Given a flow network G with source s and sink t , find a flow of maximum value from s to t

**LP formula: **$Maximize$ $\sum_{v\in V}{f(s,v)}$ $s.t$ Capacity Constarint, Flow conservation

이때, capacity 는 주어진 graph의 weights $c(u, v) = w(u,v)$

이 문제는 residual network와 augmenting path 라는 개념을 통해

Ford Fulkerson algorithm에 의해 풀릴 수 있다.

Ford Fulkerson

이 알고리즘을 설명하기전에 먼저, residual network $G_f$ 와 augmenting path의 개념을 알아야한다.

Definition of $G_f$: 주어진 flow network $G$ 와 동일한 정점과 간선을 갖는다. 그리고,

residual capacity 정의는 다음과 같다.

(주의사항: edge가 $(u,v),(v,u)$ 둘다 있을때는 $c_f(u,v) = c(u,v) - f(u,v) + f(v,u)$ ) \(c_f(u,v) = \left \{ \begin{matrix} c(u,v) - f(u,v) & \text{if } (u,v) \in E \\ f(v,u) & \text{if } (v,u) \in E \\ 0 & \text{o.w } \\ \end{matrix} \right.\)

augmenting path는 src $s$ 에서 sink $t$ 까지 모든 residual capacity가 0 이상인 simple path를 말한다.

$G_f$ 는 augmentation 연산이 superposition으로 계산될 수 있는 특성을 가진다. ($G_f$는 flow $f$에 의해 생성된 residual network 이고, $f’$ 은 $G_f$의 또 다른 flow. 따라서, flow는 포화 될때 까지 계속 augmented될 수있다.)

$f \uparrow f $ $= f + f’ $

augmentation 연산을 다음과 같다. \(f \uparrow f' (u,v) = \left \{ \begin{matrix} f(u,v) + f'(u,v) - f'(v,u) & \text{if } (u,v) \in E \\ 0 &\text{o.w} \\ \end{matrix}\right.\)

먼저, Ford-Fulkerson 방식에 대한 pseudo code

Time complexity: $O( E f^)$ , $f^$ 은 flow를 업데이트 한 총 횟수 (운이 나쁘면 매우 오래걸릴 수 있다.)

Ford-Fulkerson

Edmonds-Karp algorithm

(Ford-Fulkerson 방법의 한가지 구현 방법)

이제, 본론으로 돌아와서 Edmonds-Karp algorithm의 기본 idea는 다음과 같다.

$G_f$ 에서 $s \rightarrow t$ 로 가는 path를 찾을 때, 모든 edge들의 weight를 1로 한(unit distance로 본) BFS 알고리즘 을 이용함. DFS, BFS c++

이때 주목해야 할 intuition은 각 iteration 마다 찾아진 augmenting path 중에 적어도 한개의 edge는 saturated($c_f(e) = 0$) 되며 (왜냐하면 flow가 update 될때, $G_f$ 의 residual capacity값이 바뀌게 되는데 그에 따라 BFS 하는 방향 이 계속 바뀜 ), 점점 augmenting path의 길이는 길어진다. 이때, 증가되는 augmenting path의 최대 길이는 $V$ $-1$이기 때문에 모든 iteration에서 flow가 증가한 수$ f^* $는 $O( V   E )$ 로 bounded 된다.

pseudo code ref

Edmonds($G, s, t$)

​ $G_f \leftarrow G$

​ for each edge $(u,v)$ in $G.E$

​ $(u,v).f$ = 0

​ # iteration

​ while $\exist ~ p$ from $s$ to $t$ using $BFS(G_f)$

​ $c_f(p) = min { c_f(u, v): (u,v) ~ in ~ p}$

​ # aumentations

​ for each edge $(u,v)$ in $p$

​ if $(u,v) \in G.E$

​ $(u.v).f = (u,v).f + c_f(p)$

​ else

​ $(u.v).f = (u,v).f - c_f(p)$

time complexity: $O( V   E ^2 )$ 왜냐하면, BFS 하는데 $O( E )$, 총 flow augmented 수 $O( V   E )$

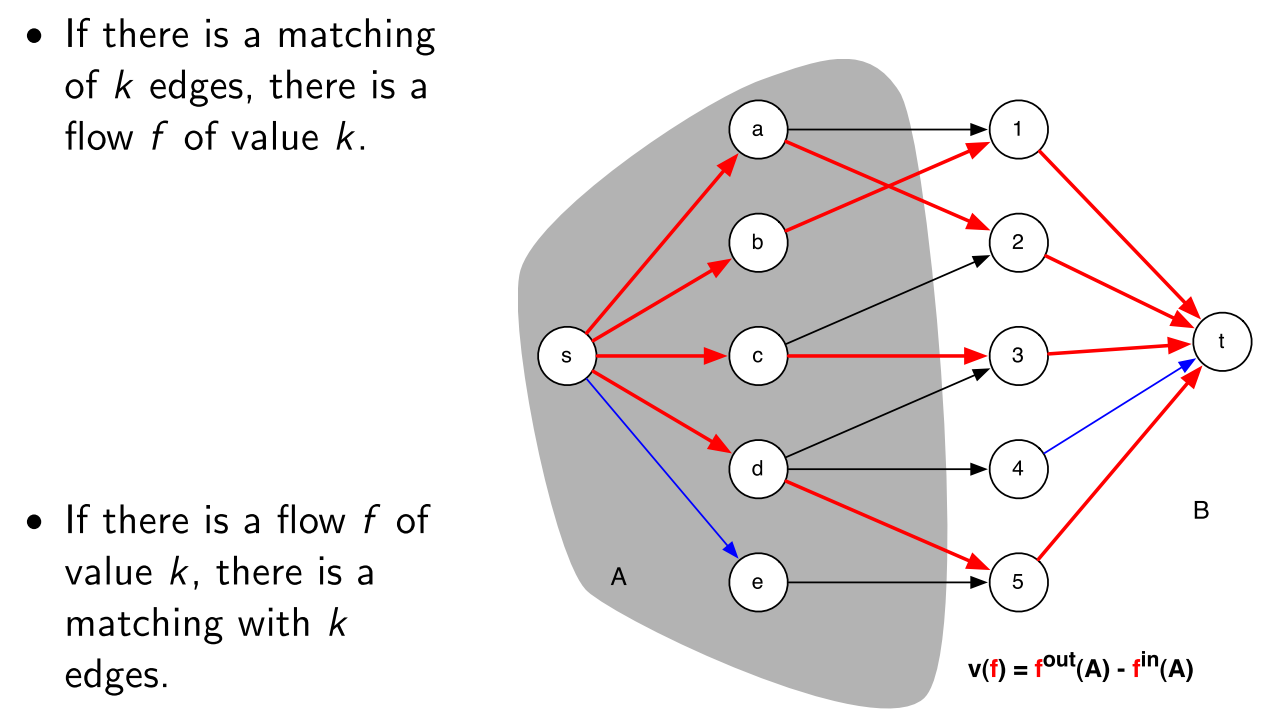
Maximum Bipartite Matching

bipartite그래프에서 최대한 많은 수의 matching3을 찾는 문제

이 문제는 Flow Maximization를 푸는 것을 이용할 수있다.

max matching size = total net flow 를 이용한다.

1
2
3
4
5
6

1 Given bipartite graph G
2 Add new vertices s and t.
3 Add an edge from s to every vertex in L.
4 Add an edge from every vertex in R to t.
5 Make all the capacities 1.
6 Solve maximum network flow problem on this new graph G'

maxmatching

pdf 영문 slide 설명

Min Cut

ST-Min Cut 문제는 directed edge weighted graph $G$의 vertex set $V$를 2개의 set $S, T$로 나누는데 $S$는 $s$를 포함한 집합, $T$는 $t$를 포함한 집합이다. 이때, $S$와 $T$를 crossing하는 edge weight를 최소화 하고 싶은게 이 문제이다.

Given an directed (edge weighted) graph $G=(V,E)$, with a source vertex $s$ and a sink vertex $t$, compute a st-cut ($S,T$) so that the sum of the crossing edge weights is the minimum.

이 문제는 Flow Maximization를 푸는 것을 이용할 수있다.

max-flow min-cut theorem (three conditions are equivalent)

  1. $f$ is a maximum flow in $G$. (flow maximization problem solution)

  2. The residual network $G_f$ contains no augmenting paths. (terminate condition of flow maximization)

  3. $ f = c(S, T)$ for some st-cut $(S, T)$ of $G$. (mincut problem solution)

    $ c(S, T) = \sum_{u \in S} \sum_{v \in T}{c(u,v)}$ ,여기서 $c(u,v)$ 는 residual capacity of $(u,v)$

Proof. We will prove 3 $\Rightarrow$ 1, 1 $\Rightarrow$ 2, 2 $\Rightarrow$ 3

(3 $\Rightarrow$ 1) From the capacity constraint, any flow f and any st-cut $(S’, T’)$, we have that $|f| ≤ c(S’, T’).$ \(\begin{aligned} \mbox{total net flow } |f| &= \sum_{u\in S'}\sum_{v\in T'}{f(u,v)} - \sum_{v\in S'}\sum_{u\in T'}{f(v,u)} \\ &\le \sum_{u\in S'}\sum_{v\in T'}{f(u,v)} &\because |f| \ge 0 \\ &\le \sum_{u\in S'}\sum_{v\in T'}{c(u,v)} &\because f(u,v) \le c(u,v)\\ &= c(S',T') \end{aligned}\)

From this inequality, $ f =c(S’, T’)$ implies $f$ is max flow. Thus, we have that 3 $\Rightarrow$ 1.

(1 $\Rightarrow$ 2) 모순을 이끌어 내기 위한 가정으로 1은 True인데, 2는 False라고 가정해보자.

즉, $f$ 는 $G$의 max flow인데, $G_f$ 는 augmenting path $f’$를 가진하고 하자.

그러면, $G_f$의 augmenting path $f’$을 더 함으로서 $ f+f’ = f + f’ $ property에 의해 $f$를 증가시킬 수 있다.

이 상황에서, 우리는 1 이 False($f$는 더이상 max flow가 아님)가 된다.

따라서, 모순이므로, 1이 True면 2는 반드시 True여야한다.

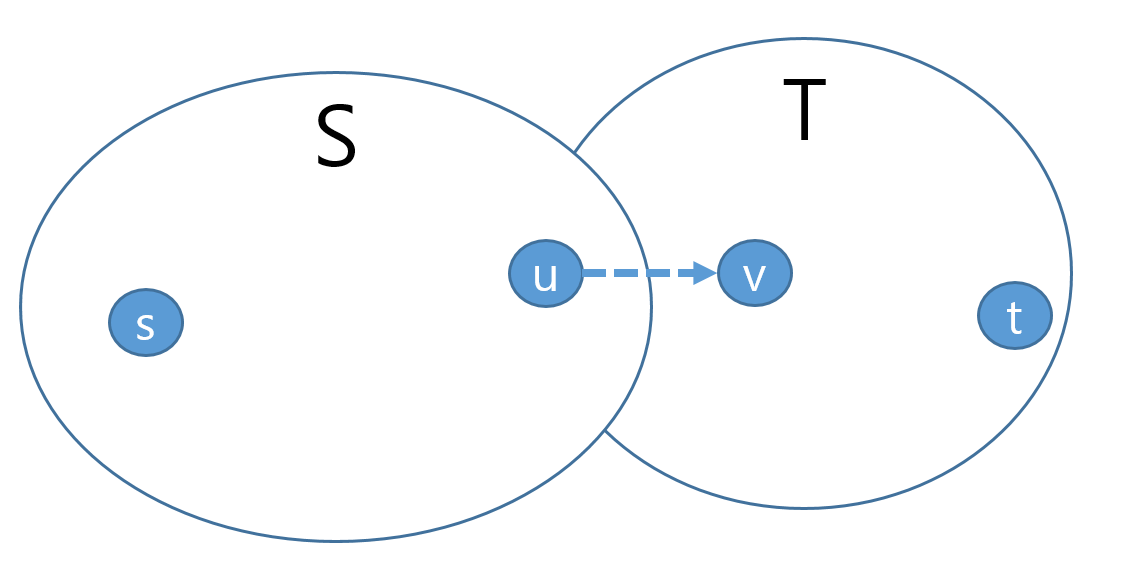
(2 $\Rightarrow$ 3) Let $S$ to be the set of vertices in $G$ that is reachable from $s$ by a path with positive edge capacities (of $G_f$), and let $T = V − S$.

mincut

2가 True이면 augmenting path가 더이상 없으므로 T에 속한 v 에 절대 reachable 할수 없다. 그래서, $ f = c(S,T)$ (3 도 True)라고 할 수 있다.

만약 2가 True가 아니라면, augmenting path가 있다는 것이고, 그말은 즉슨, residual capacity 보다 작은 flow f(u,v) 가 존재한다는 뜻( $\exist f(u,v) < c(u,v)$)이여서 $u$에서 $v$로 갈수 있는 augmenting path가 존재하게 되어 T에 속한 v 에 reachable 할수있게 된다. 즉,2가 False 가 되는 모순이 되므로 반드시 2가 True인 상태에서 3 이 True 가 된다.

Max Cut

Efficient algorithm: Goemans and Williamson (Approximate algorithm)

Approximate algorithm에서 다루도록 하겠다.

Reference

  1. 어떤 그래프가 connected 되었다는건 모든 정점들 간에 path가 반드시 존재하는 그래프 ↩

  2. 최상의 정점(중심)을 루트(Root Node)로 하고, 모든 그룹 멤버들을 자손으로 갖는 트리구조 ↩

  3. A matching in a graph is a subset of its edges, no two of which share an endpoint. ↩

Leave a comment

You may also enjoy

Reeds-Shepp (RS) Path

18 minute read

이동체의 운동 구속조건을 반영하면 전진과 후진 경로에 대한 48가지 경로의 조합을 체크하는 RS path를 배워보자.

Model Predictive Control (MPC)

17 minute read

motion model로 다음 상태를 예측하여 비용함수를 만들고 모델을 제약사항으로 최적화를 하여 제어값을 찾아내는 MPC에 대해서 배워보자

RRT star

15 minute read

RRT star 알고리즘에 대해서 알아보자.