1
2
3
4
5
6
7
8
9
import sys, random, string
sys.path.append("/home/swyoo/algorithm/")
from utils.verbose import visualize_graph, logging_time
from utils.generator import randomString
from collections import defaultdict
from pprint import pprint
from copy import deepcopy
from typing import List, Tuple
import numpy as np
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
def generate_graph(n, m, randrange:Tuple[int, int], verbose=False):
""" |V|: n, |E|: m """
# S = set(' '.join(string.ascii_lowercase).split()[:n])
S = set(range(n))
seen = set()
edges = []
for _ in range(m):
while True:
# start = randomString(length=1, samples=list(S))
# end = randomString(length=1, samples=list(S - {start}))
while True:
start, end = random.choices(population=range(n - 1), k=2)
if start != end: break
if (start, end) not in seen:
seen.add((start, end))
break
edges.append((start, end, random.randint(randrange[0], randrange[1])))
if verbose: visualize_graph(edges, weighted=True)
graph = defaultdict(list)
for i in S: graph[i]
for u, v, w in edges:
graph[u].append((v, w))
return graph, edges
INF = 1e20
def g2m(graph):
n, nodes = len(graph.keys()), sorted(graph.keys())
n2i = {k: v for k, v in zip(nodes, range(n))}
weights = [[INF] * n for _ in range(n)]
for i in nodes: weights[n2i[i]][n2i[i]] = 0
for i in nodes:
for j, w in graph[i]:
weights[n2i[i]][n2i[j]] = w
return n2i, weights
def hasNcycles(weights, verbose=False):
n = len(weights)
ans = deepcopy(weights)
for k in range(n):
for i in range(n):
for j in range(n):
ans[i][j] = min(ans[i][j], ans[i][k] + ans[k][j])
# check if negative cycle exist
for i in range(n):
if ans[i][i] < 0:
if verbose: print("negative cycle exists from node[{}] to node[{}]".format(i, i))
return True
return False
def generate_graph_no_neg_cycle(n, m, randrange):
weights = graph = None
while True:
graph, edges = generate_graph(n, m, randrange, verbose=False)
n2i, W = g2m(graph)
if not hasNcycles(W):
weights = deepcopy(W)
return n2i, weights, graph, edges
n, m = 5, 7
n2i, weights, graph, edges = generate_graph_no_neg_cycle(n, m, randrange=(-10, 100))
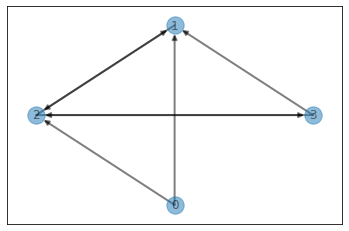
visualize_graph(edges=edges, weighted=True)
graph
1
2
3
4
5
6
defaultdict(list,
{0: [(1, 48), (2, -9)],
1: [(2, 0)],
2: [(1, 72), (3, 26)],
3: [(1, 3), (2, 95)],
4: []})
Bellman Ford
기본가정: no negative weight cycle(있다면 False return)
Dijkstra’s algorithm과 달리 Bellman Ford 알고리즘은 가중치가 음수인 경우에도 적용 가능.
음수 가중치가 사이클(cycle)을 이루고 있는 경우에는 작동하지 않는다.
naive 하게 그래프 정점 수만큼 그래프 내 모든 엣지에 대해 edge relaxation을 수행한다.
그러면 (negative weight cycle 이 없다는 가정하에) 모든 정점수 만큼의 relaxation을 돌았을때, shortest path를 찾을 수 있다.
Pseudo Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Bellman(G, s)
# shortest distance 값을 저장할 array
let d[1 ..|G.V|] be a new array
# initialization
d[k] = INF for all k in G.V except for k == s
d[s] = 0
# edge relaxations for all cases O(VE)
for i = 1 to |G.V|
for (u,v) in G.E
if d[v] > d[u] + w(u,v)
d[v] = d[u] + w(u,v)
# check whether eixist negative weight cycle
# negative weight cycle 가 있다면 edge relaxation을 했을때
# shortest path distance보다 작은 distance 가 존재 할 것이다.
for (u,v) in G.E
if d[v] > d[u] + w(u,v)
return False
return d
Time Complexity
모든 cases 에 대해 edge relaxation을 수행해야하므로 $T(n) =O(VE)$
Implementation
graph 의 엣지정보인 edges와 노드의 총 개수 $n$ 만 알면 된다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
INF = 1e20
n = len(graph.keys())
@logging_time
def bellman(src, edges, n):
ans = [INF] * n
ans[src] = 0
for _ in range(n):
for i, j, w in edges:
ans[j] = min(ans[j], ans[i] + w)
for i, j, w in edges:
if ans[j] > ans[i] + w:
return False # detect negative weight cycle.
return ans
1
2
3
4
5
6
7
n, m = 5, 7
n2i, weights, graph, edges = generate_graph_no_neg_cycle(n, m, randrange=(-10, 100))
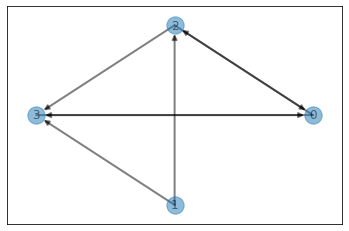
visualize_graph(edges=edges, weighted=True)
pprint(graph)
print(edges)
print("after run bellman ford algorithm ...")
bellman(0, edges, n, verbose=True)
1
2
3
4
5
6
7
8
9
10
defaultdict(<class 'list'>,
{0: [(2, 86), (3, 99)],
1: [(2, 79), (3, 23)],
2: [(3, 54), (0, 29)],
3: [(0, 0)],
4: []})
[(0, 2, 86), (0, 3, 99), (2, 3, 54), (2, 0, 29), (1, 2, 79), (3, 0, 0), (1, 3, 23)]
after run bellman ford algorithm ...
WorkingTime[bellman]: 0.01311 ms
1
[0, 1e+20, 86, 99, 1e+20]
Application
It can be used to detect negative weight cycle like floyd warshall algorithm!
DAG
Topological sort를 사용하여 Bellman Ford 를 좀더 개선한 방식
기본가정: Topological sort를 사용해야하므로 DAG에 대해서만 사용가능
Bellman ford 알고리즘은 naive하게 모든 가능한 경우의 수에 대해서 edge relaxation 을 수행하였다.
DAG algorithm은 좀더 효율적이게 topolgical sort를 한 순서의 정점 리스트에 대해서
adjacent list 를 바탕으로 edge relaxation을 수행
Pseudo Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Bellman(g, s)
let d[1 ..|G.V|] be a new array
# initialization
d[k] = INF for all k in G.V except for k == s
d[s] = 0
# edge relaxations for a efficient way
L = TopoSort(G);
for u in L
for (u,v) in G.adj[u]
if d[v] > d[u] + w(u,v)
d[v] = d[u] + w(u,v)
return d
Topological sort를 한 List 순으로 진행되므로 $T(n) =O(V + E)$
Step1. Generate DAG and Topological Sort
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def toposort(g:dict):
seen, finish = set(), set()
topo = []
hascycle = False
def dfs(i):
nonlocal hascycle
seen.add(i)
for j, w in g[i]:
if j not in seen:
dfs(j)
elif j not in finish:
hascycle = True
return
topo.append(i), finish.add(i)
for i in g.keys():
if i not in seen:
dfs(i)
return topo[::-1], hascycle
toposort(graph)
1
([4], True)
1
2
3
4
5
6
7
8
def generate_graph_no_cycle(n, m, randrange):
weights = graph = None
while True:
graph, edges = generate_graph(n, m, randrange, verbose=False)
n2i, W = g2m(graph)
if not toposort(graph)[1]:
weights = deepcopy(W)
return n2i, weights, graph, edges
1
2
3
n2i, weights, graph, edges = generate_graph_no_cycle(6, 10, randrange=(-10, 30))
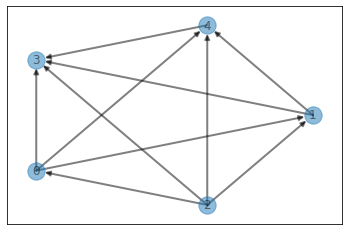
visualize_graph(edges, weighted=True)
pprint(graph)
1
2
3
4
5
6
7
8
defaultdict(<class 'list'>,
{0: [(1, -10), (4, 24), (3, 0)],
1: [(4, 10), (3, -5)],
2: [(0, 29), (4, -6), (3, 1), (1, 21)],
3: [],
4: [(3, 15)],
5: []})
1
toposort(graph)
1
([5, 2, 0, 1, 4, 3], False)
Step 2. DAG Algorithm
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
INF = 1e20
@logging_time
def DAG(src, g, n):
def toposort(g:dict):
seen, finish, topo, hascycle = set(), set(), [], False
def dfs(i):
nonlocal hascycle
seen.add(i)
for j, w in g[i]:
if j not in seen:
dfs(j)
elif j not in finish:
hascycle = True
return
topo.append(i), finish.add(i)
for i in g.keys():
if i not in seen:
dfs(i)
return topo[::-1], hascycle
ans = [INF] * n
ans[src] = 0
L, hascycle = toposort(g)
for i in L:
for j, w in g[i]:
ans[j] = min(ans[j], ans[i] + w)
return ans if not hascycle else False
1
2
3
4
5
n2i, weights, graph, edges = generate_graph_no_cycle(6, 10, randrange=(-10, 30))
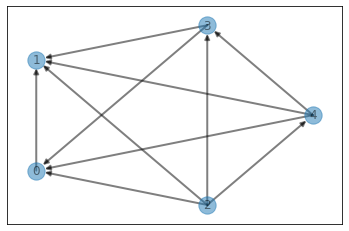
visualize_graph(edges, weighted=True)
pprint(graph)
n = len(graph.keys())
DAG(src=0, g=graph, n=n, verbose=True)
1
2
3
4
5
6
7
8
9
defaultdict(<class 'list'>,
{0: [(1, 6)],
1: [],
2: [(1, 10), (3, -5), (4, -9), (0, -3)],
3: [(1, 8), (0, 28)],
4: [(3, -4), (1, 6), (0, -6)],
5: []})
WorkingTime[DAG]: 0.01574 ms
1
[0, 6, 1e+20, 1e+20, 1e+20, 1e+20]
1
2
for i in graph.keys():
print(DAG(src=i, g=graph, n=n, verbose=False)[0])
1
2
3
4
5
6
7
[0, 6, 1e+20, 1e+20, 1e+20, 1e+20]
[1e+20, 0, 1e+20, 1e+20, 1e+20, 1e+20]
[-15, -9, 0, -13, -9, 1e+20]
[28, 8, 1e+20, 0, 1e+20, 1e+20]
[-6, 0, 1e+20, -4, 0, 1e+20]
[1e+20, 1e+20, 1e+20, 1e+20, 1e+20, 0]
Ballman Ford vs DAG
비교를 위해서는 두 알고리즘을 돌리기 위한 제한사항을 둘다 만족해야한다.
따라서, cycle이 없는 두 그래프를 만든 후, 비교하겠다.
1
2
3
4
5
6
n2i, weights, graph, edges = generate_graph_no_cycle(300, 400, randrange=(-10, 30))
visualize_graph(edges, weighted=True)
n = len(weights)
ans1 = bellman(0, edges, n, verbose=True)
ans2 = DAG(src=0, g=graph, n=n, verbose=True)
assert ans1 == ans2

1
2
3
WorkingTime[bellman]: 28.24116 ms
WorkingTime[DAG]: 0.32878 ms
Reference
[1] Floyd Warshall
[2] Topological Sort


Leave a comment