1
2
3
4
5
6
7
8
9
10
import sys, random
sys.path.append("/home/swyoo/algorithm/")
from utils.generator import generate_graph, generate_graph_no_neg_cycle
from utils.verbose import logging_time
from binarytree import build
from pprint import pprint
plot = lambda a: build(a).pprint()
from heapq import heappop, heappush, heappushpop, heapify
from collections import defaultdict, OrderedDict
Dijstra Algorithm
기본가정: 모든 edge가 non-negative weight 이어야함 (가중치가 음수인 경우 작동하지 않는다)
priority queue 를 이용한 알고리즘
Pseudo Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Dijkstra(G, s)
# initialization
k.d = INF for all k in G.V except for k == s
s.d = 0
# vertices in set S have already shortest path distance
create set S
# priority queue Q(min heap)의 {key=vertex, value=vertex.d]}
# value가 낮을 수록 priority is higher
create priority queue Q
Q ← all G.V
while !Q.empty()
u = Q.pop()
S ← u
for v in G.adj[u]
if v not in S and v.d > u.d + w(u,v)
v.d = u.d + w(u,v)
# update distance of v in O(log|V|)
Q.update_value(v, v.d)
$S$는 shortest path가 결정된 node들을 keep track 할때 쓰이므로 꼭 필요하진 않으므로 생략해도 된다.
Time complexity: $O((|V|+|E|)log|V|)$
1
2
n, m = 5, 7
graph, edges, nodes = generate_graph(n, m, randrange=(0, 100), character=True, verbose=True)
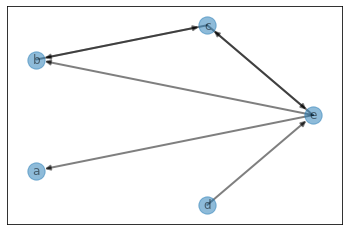
1
graph
1
2
3
4
5
defaultdict(list,
{'e': [('c', 93), ('b', 54), ('a', 54)],
'b': [('c', 81)],
'c': [('e', 73), ('b', 36)],
'd': [('e', 85)]})
1
nodes
1
{'a', 'b', 'c', 'd', 'e'}
Implementation
single source shortest path를 구한다.
주목할 점은 heap에서 뽑혀나온 노드 i 의 인접한 노드 j 에 대해 heap에 distance 를 update 해야하는데
heap에서 j의 위치를 알아야 update할 수있다. (update하는 방법은 예를 들면 지웠다가 새로운 노드를 넣으면 됨).
그런데, heap에서 j의 위치를 아는데 (heappush, heappop를 heapq라이브러리를 가져다가 사용하여서)
heappush, heappop 내부 함수에 추적하는것을 구현 해놓지 않았으므로 $O(n)$이 걸리게 된다.
우리가 원하는 것은 $O(logn)$에 업데이트 해야한다.
update를 구현하지 않고도 어느정도 잘 동작하도록 하는 방법은 그냥 update할 새로운 값을 push하는 것이다.
왜 이것이 가능하냐면, 어짜피 heap에서 최소의 값을 우선순위로 선택하기 때문에 distance가 높은 값들은 나중에야 pop된다.
따라서, 우선순위가 낮은 값들은 shortest path를 찾는데는 영향을 끼치지 못한다.
하지만, 이렇게 구현하면 최악의 경우에 $O(n^2)$인 dijkstra algorithm이 된다.
그것이 싫다면, heap에서 노드의 위치를 O(1)에 바로 알수 있도록 구현하여야한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
INF = 1e20
def dijstra(G, nodes, src, show=False):
dist = defaultdict(lambda: INF)
dist[src] = 0
Q = [(dist[e], e) if e != src else (0, src) for e in nodes]
heapify(Q)
if show:
plot(map(lambda e: e[0], Q))
print(Q)
while Q:
d, i = heappop(Q)
for j, w in G[i]:
if d + w < dist[j]:
dist[j] = d + w
heappush(Q, (dist[j], j))
if show: print(dist)
return dist
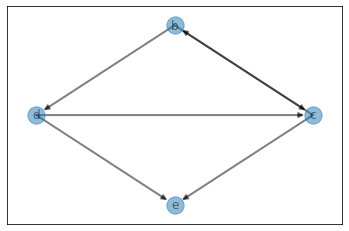
n, m = 5, 6
graph, edges, nodes = generate_graph(n, m, randrange=(0, 100), character=True, verbose=True)
pprint(graph)
src = random.choice([e for e in nodes])
print("src={}".format(src))
print("start dijkstra algorithm ... ")
ans = dijstra(graph, nodes, src, show=True)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
defaultdict(<class 'list'>,
{'b': [('c', 97), ('d', 40)],
'c': [('b', 88), ('e', 61)],
'd': [('e', 66), ('c', 97)]})
src=b
start dijkstra algorithm ...
__0__
/ \
__1e+20 1e+20
/
1e+20
[(0, 'b'), (1e+20, 'd'), (1e+20, 'c'), (1e+20, 'e')]
defaultdict(<function dijstra.<locals>.<lambda> at 0x7fa5365a8ef0>, {'b': 0, 'c': 97, 'd': 40, 'e': 106})
Improved
heap에서 노드의 위치를 pos dictionary mapping을 사용해서 바로 추적할 수 있도록 구현하자.
1
min([(50, 20),(20, 30), (40, 10)])
1
(20, 30)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
INF = 1e20
def improved(G, nodes, src, show=False):
pos = OrderedDict()
def _down(a, i):
left, right, n = 2 * i, 2 * i + 1, len(a)
if left > n - 1: return
smallest = min([k for k in [left, right, i] if k < n], key=lambda idx: a[idx])
if i != smallest:
a[smallest], a[i] = a[i], a[smallest]
pos[a[smallest][1]], pos[a[i][1]] = pos[a[i][1]], pos[a[smallest][1]]
_down(a, smallest)
def build(a):
for i in range((len(a) // 2) , -1, -1):
_down(a, i)
def heappop(a, i):
new, old = a[-1], a[i]
n = len(a)
pos.pop(a[i][1])
a[i] = a[n - 1]
pos[a[n - 1][1]] = i
a.pop()
if n > 1:
_up(a, i) if new[0] < old[0] else _down(a, i)
return old
def _up(a, i):
up = (i - 1) // 2
if up < 0: return
if a[up] > a[i]:
a[up], a[i] = a[i], a[up]
pos[a[up][1]], pos[a[i][1]] = pos[a[i][1]], pos[a[up][1]]
_up(a, up)
def heappush(a, item):
a.append(item)
pos[a[-1][1]] = len(a) - 1
_up(a, len(a) - 1)
dist = defaultdict(lambda: INF)
dist[src] = 0
Q = [(dist[e], e) if e != src else (0, src) for e in sorted(nodes)]
for i, item in enumerate(Q):
key, name = item
pos[name] = i
build(Q)
while Q:
if show:
plot(map(lambda e: e[0], Q))
print(Q)
print(pos)
d, i = heappop(Q, 0)
for j, w in G[i]:
if d + w < dist[j]:
dist[j] = d + w
heappop(Q, pos[j])
heappush(Q, (dist[j], j))
if show: print(dist)
return dist
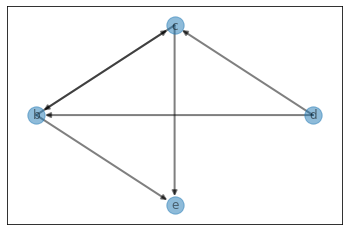
n, m = 5, 6
graph, edges, nodes = generate_graph(n, m, randrange=(0, 100), character=True, verbose=True)
pprint(graph)
src = random.choice([e for e in nodes])
print("src={}".format(src))
print("start dijkstra algorithm ... ")
# ans1 = dijstra(graph, nodes, src, show=True)
ans2 = improved(graph, nodes, src, show=True)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
defaultdict(<class 'list'>,
{'b': [('e', 99), ('c', 22)],
'c': [('e', 74), ('b', 5)],
'd': [('c', 83), ('b', 80)]})
src=d
start dijkstra algorithm ...
__0__
/ \
__1e+20 1e+20
/
1e+20
[(0, 'd'), (1e+20, 'b'), (1e+20, 'c'), (1e+20, 'e')]
OrderedDict([('b', 1), ('c', 2), ('d', 0), ('e', 3)])
__80
/ \
1e+20 83
[(80, 'b'), (1e+20, 'e'), (83, 'c')]
OrderedDict([('e', 1), ('c', 2), ('b', 0)])
_83
/
179
[(83, 'c'), (179, 'e')]
OrderedDict([('c', 0), ('e', 1)])
157
[(157, 'e')]
OrderedDict([('e', 0)])
defaultdict(<function improved.<locals>.<lambda> at 0x7fa53648c9e0>, {'d': 0, 'b': 80, 'c': 83, 'e': 157})
All pair shortest path
모든 vertices를 source로 두고 dijstra 알고리즘을 적용하면 All pair shortest path를 구할 수있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def solve(G, nodes, show=False):
n = len(nodes)
n2i = dict(zip(sorted(nodes), range(n)))
D = [[INF] * n for _ in range(n)]
for src in nodes:
dist = improved(G, nodes, src, show=show)
for end, ans in dist.items():
D[n2i[src]][n2i[end]] = ans
print("n2i:",n2i)
pprint(D)
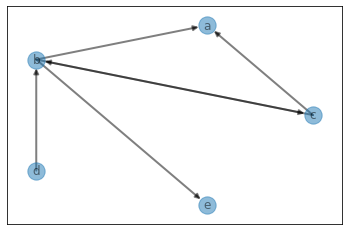
n, m = 5, 6
graph, edges, nodes = generate_graph(n, m, randrange=(0, 100), character=True, verbose=True)
pprint(graph)
ans = solve(graph, nodes)
pprint(ans)
1
2
3
4
5
6
7
8
9
10
11
12
defaultdict(<class 'list'>,
{'b': [('a', 23), ('c', 90), ('e', 21)],
'c': [('a', 3), ('b', 79)],
'd': [('b', 85)]})
n2i: {'a': 0, 'b': 1, 'c': 2, 'd': 3, 'e': 4}
[[0, 1e+20, 1e+20, 1e+20, 1e+20],
[23, 0, 90, 1e+20, 21],
[3, 79, 0, 1e+20, 100],
[108, 85, 175, 0, 106],
[1e+20, 1e+20, 1e+20, 1e+20, 0]]
None
Dijkstra Algorithm Correctness Proof
proof by Induction 을 통해 증명하겠다.
loop invariant 는 매 iteration의 시작점에서 $u.d = \delta(s,u)$ 즉, shortest path distance
다음 그림을 보면서 이해

shortest path 가 결정된 vertex 집합을 $S$라 하고, 매 iteration 마다 정점 하나씩 추가된다.
Base Case
시작점 source vertex의 shortest distance 는 0이므로 $s.d = \delta(s,s) = 0$ correct
Induction step:
임의의 iteration 이전까지는 S안에 shortest path distance들이 결정된 vertex들만 들어가다가
dijkstra 알고리즘에의해 처음으로 $\color{red}u.d \neq \delta(s.u)$ 인 $\color{red}u$가 queue에서 뽑혔다고 하자.(모순을 이끌어내겠다.)
이때, $s$부터 $u$ 까지의 shortest path에서 $S$의 경계점 바로 직전과 직후의 정점 $x$와 $y$ 를 생각해 보자.
일단. $x.d = \delta(s,x)$ 가 자명하다($S$가 shortest path distance가 결정된 정점 집합이라고 했으므로)
그래서, $y.d = \delta(s,x) + w(x,y) = \delta(s,y)$ 는 shortest distance 인 상황이며,
이 사실과 negative edge가 없다는 사실로부터 ($\delta(y,u) \ge 0$)
\(\begin{aligned}
u.d &> \delta(s,u) = y.d + \delta(y,u)\ge y.d \\
\therefore u.d &> y.d
\end{aligned}\)
임을 주목해보자.
이 상황에서, 우리의 처음 가정이 맞다면, $u.d \le y.d $이어야한다.
( dijkstra 알고리즘에의해 처음으로 $u.d \neq \delta(s.u)$ 인 u가 queue에서 뽑혔다고 했으므로 $u.d$가 같거나 더 작아야한다.)
하지만, 그렇지 않기 때문에 모순이 된다.
따라서, $\color{red}u.d = \delta(s,u)$ 인 $\color{red}u$가 뽑혀야만 한다.
Application
leetcode problem - Network Delay Time3
Use library heapq
\(T(n) = O(n^2)\)
https://leetcode.com/submissions/detail/354416404/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
from typing import List
from collections import defaultdict
from heapq import heapify, heappush, heappop
class Solution:
@logging_time
def networkDelayTime(self, times: List[List[int]], N: int, K: int) -> int:
""" warning: node index should be -1. """
INF = 1e20
graph = defaultdict(list)
for i, j, w in times:
graph[i - 1].append((j - 1, w))
dist = [INF if i != (K - 1) else 0 for i in range(N)]
Q = [(dist[i], i) for i in range(N)]
heapify(Q)
while Q:
# plot(map(lambda e: e[0], Q))
d, i = heappop(Q)
for j, w in graph[i]:
if d + w < dist[j]:
dist[j] = d + w
heappush(Q, (dist[j], j))
res = set(dist)
return max(res) if INF not in res else -1
times, N, K = [[2,1,1],[2,3,1],[3,4,1]], 4, 2
sol1 = Solution()
print(sol1.networkDelayTime(times, N, K, verbose=True))
1
2
3
WorkingTime[networkDelayTime]: 0.01597 ms
2
Customized Heap
\[T(n) = O(nlogn)\]https://leetcode.com/submissions/detail/354416104/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
from typing import List
from collections import defaultdict, OrderedDict
class Custom:
@logging_time
def networkDelayTime(self, times: List[List[int]], N: int, K: int) -> int:
""" warning: node index should be -1. """
INF = 1e20
pos = OrderedDict()
def _down(a, i):
left, right, n = 2 * i + 1, 2 * i + 2, len(a)
if left > n - 1: return
smallest = min([k for k in [left, right, i] if k < n], key=lambda idx: a[idx])
if i != smallest:
a[smallest], a[i] = a[i], a[smallest]
pos[a[smallest][1]], pos[a[i][1]] = pos[a[i][1]], pos[a[smallest][1]]
_down(a, smallest)
def build(a):
for i in range((len(a) // 2), -1, -1):
_down(a, i)
def heappop(a, i):
new, old = a[-1], a[i]
n = len(a)
pos.pop(a[i][1])
a[i] = a[n - 1]
pos[a[n - 1][1]] = i
a.pop()
if n > 1:
_up(a, i) if new[0] < old[0] else _down(a, i)
return old
def _up(a, i):
up = (i - 1) // 2
if up < 0: return
if a[up] > a[i]:
a[up], a[i] = a[i], a[up]
pos[a[up][1]], pos[a[i][1]] = pos[a[i][1]], pos[a[up][1]]
_up(a, up)
def heappush(a, item):
a.append(item)
pos[a[-1][1]] = len(a) - 1
_up(a, len(a) - 1)
graph = defaultdict(list)
for i, j, w in times:
graph[i - 1].append((j - 1, w))
dist = [INF if i != (K - 1) else 0 for i in range(N)]
Q = [(dist[i], i) for i in range(N)]
for i, item in enumerate(Q):
_, name = item
pos[name] = i
build(Q)
while Q:
d, i = heappop(Q, 0)
# if Q: plot(map(lambda e: e[0], Q))
for j, w in graph[i]:
if d + w < dist[j]:
dist[j] = d + w
heappop(Q, pos[j])
heappush(Q, (dist[j], j))
res = set(dist)
return max(res) if INF not in res else -1
times, N, K = [[2,1,1],[2,3,1],[3,4,1]], 4, 2
sol2 = Custom()
print(sol2.networkDelayTime(times, N, K, verbose=True))
1
2
3
WorkingTime[networkDelayTime]: 0.04482 ms
2
1
2
3
4
5
6
7
n, m = random.randint(1, 100), random.randint(1, 6000)
_, edges, nodes = generate_graph(n, m, randrange=(1, 100), verbose=False)
n, m = len(nodes), len(edges)
K = random.randint(1, n)
print(n, m, K)
ans1 = sol1.networkDelayTime(times, n, K, verbose=True)
ans2 = sol2.networkDelayTime(times, n, K, verbose=True)
1
2
3
4
42 1347 20
WorkingTime[networkDelayTime]: 0.04935 ms
WorkingTime[networkDelayTime]: 0.33307 ms


Leave a comment