Frevialds Algorithms for checking Matrix Multiplication randomly

In [1]:

import sys
import numpy as np
import random, math
import matplotlib.pyplot as plt
sys.path.append("/home/swyoo/algorithm/")
from utils.verbose import logging_time, printProgressBar

In [2]:

# sys.stdin = open('input.txt')
# n = int(sys.stdin.readline())
# a = [list(map(int, sys.stdin.readline().split())) for _ in range(n)]
# b = [list(map(int, sys.stdin.readline().split())) for _ in range(n)]
# c = [list(map(int, sys.stdin.readline().split())) for _ in range(n)]

# toy example at wikiwand
a = [[2, 3],[3, 4]]
b = [[1, 0],[1, 2]]
c = [[6, 5],[8, 7]]

Naive

Time Complexity

\(O(n^3)\)

In [3]:

@logging_time
def naive(a, b, c):
    """ naive approach """
    def matmul(x, y):
        assert len(x) == len(y), "x, y shapes not matched!"
        n = len(x)
        res = [[-1 for _ in range(n)] for _ in range(n)]
        for i in range(n):
            for j in range(n):
                res[i][j] = 0
                for k in range(n):
                    res[i][j] += x[i][k] * y[k][j]
        return res
    return matmul(a, b) == c

In [4]:

naive(a, b, c, verbose=True)

WorkingTime[naive]: 0.01073 ms

(False, 0.010728836059570312)

Freivalds’ Algorithm

Randomized algorithm to determine whether $\textbf{A}\textbf{B} = \textbf{C}$ is True or False.
, where $\textbf{A}, \textbf{B}, \textbf{C}$ are $n \times n$ matrix.

Freivalds’ algorithm utilizes randomization in order to reduce this time bound to $O(n^{2})$ with high probability.

Key Idea

• Check if $\textbf{A}\textbf{B}\textbf{r} = \textbf{C}\textbf{r}$, where $\textbf{r}$ is a size $n$ vector with each element 0 or 1 (randomly, equally likely generated).
• The randomly generated vector $\textbf{r}$ determines the output with bounded error probability $1/2$.
• The error probability is decayed exponentially as checking process repeat (proved on later).

In our toy example above, we can notice the intuition.
when $\textbf{r} = \begin{bmatrix} 1\ 1 \end{bmatrix}$, $\textbf{A}\textbf{B}\textbf{r} - \textbf{C}\textbf{r} = \begin{bmatrix} 0\ 0 \end{bmatrix}$.
However, when $\textbf{r} = \begin{bmatrix} 1\ 0 \end{bmatrix}$, $\textbf{A}\textbf{B}\textbf{r} - \textbf{C}\textbf{r} = \begin{bmatrix} -1\ -1 \end{bmatrix}$.

Among cases of $\textbf{r} =$ ($\begin{bmatrix} 0\ 0 \end{bmatrix}, \begin{bmatrix} 1\ 0 \end{bmatrix}, \begin{bmatrix} 0\ 1 \end{bmatrix}, \begin{bmatrix} 1\ 1 \end{bmatrix}$), the cases ($\begin{bmatrix} 0\ 0 \end{bmatrix}, \begin{bmatrix} 1\ 1 \end{bmatrix}$) lead to $\begin{bmatrix} 0\ 0 \end{bmatrix}$.
which means, 1/2 cases lead to non-zeros vector, which is the error probability.
We can notice that the result is True only when $\textbf{A}\textbf{B}\textbf{r} - \textbf{C}\textbf{r} = \begin{bmatrix} 0\ 0 \end{bmatrix}$ ,$\forall \textbf{r}$.

Time Complexity

\(O(n^2)\)

In [5]:

def freivald(a, b, c):
    """ check if (abr == cr) for one iteration, with probability 1/2.
    n is dim of a, b, c, where they are square matrix."""
    assert len(a) == len(b), "x, y shapes not matched!"
    n = len(a)
    
    r = [random.randint(0, 1) for _ in range(n)]
    # print(r)

    br = [0] * n
    for i in range(n):
        for j in range(n):
            br[i] += b[i][j] * r[j]

    abr = [0] * n
    for i in range(n):
        for j in range(n):
            abr[i] += a[i][j] * br[j]

    cr = [0] * n
    for i in range(n):
        for j in range(n):
            cr[i] += c[i][j] * r[j]

    # check if non-zero exist
    for i in range(n):
        if abr[i] - cr[i] != 0:
            return False
    return True

@logging_time
def check(a, b, c, k):
    """ error probabilities is decayed exponentially as checking process repeats
    when # of iteration is k, P[error] <= 2^{-k}"""
    for _ in range(k):
        if not freivald(a, b, c):
            return False
    return True

In [6]:

check(a, b, c, 2, verbose=True)

WorkingTime[check]: 0.03672 ms

(False, 0.036716461181640625)

Error Analysis

Note that All elements of $\textbf{A}\textbf{B} - \textbf{C}$ should be $0$ if matched case is happened.
We generate $\textbf{r}$ and use it for checking process to reduce time complexity.
How can this algorithm do that?

Let’s prove that algorithm’s $P[error] \le 1/2$.

• Case 1: $\textbf{A}\textbf{B} = \textbf{C}$
  If a non-zero element exist in the result of $\textbf{A}\textbf{B}\textbf{r} - \textbf{C}\textbf{r}$, it is error. However, this case is not going to be happended.
  This is because
  $\textbf{A}\textbf{B}\textbf{r} - \textbf{C}\textbf{r}$ always $\begin{bmatrix} 0 …0 \end{bmatrix}$.
  Therefore, error cases never happen, so $P[error]$ = 0
• Case 2: $\textbf{A}\textbf{B} \neq \textbf{C}$
  Let $\textbf{A}\textbf{B} - \textbf{C}$ be $\textbf{D}$.
  $\textbf{A}\textbf{B}\textbf{r} - \textbf{C}\textbf{r} =\textbf{D}\textbf{r}$ is not $\begin{bmatrix} 0 …0 \end{bmatrix}$, which is represented as $\begin{bmatrix} p_1\ …\ p_n \end{bmatrix}$ because non zero $d_{ij} \neq 0, \exists (i, j)$, where $d_{ij} \in D$
  Assume that $d_{ij} \neq 0$. ($y$ is a constant)
  \(p_i=\sum_{k=1}^{n}{d_{ik}r_k} = d_{ij}r_j + y\) If all $p_i$ become $0$, it is error.
  Therefore, the bound of error probability is computed as follows. \(\begin{align} P[\bigcap_{1 \le i \le n}{(p_i = 0)}] &\le P[p_i = 0] \\ & = P[p_i=0|y=0]P[y=0] + P[p_i=0|y\neq0]P[y\neq0] \\ & = P[r_j=0]P[y=0] + P[r_j=1 \cap d_{ij} = -y]P[y\neq0] \\ & \le P[r_j=0]P[y=0] + P[r_j=1]P[y\neq0] \\ & = \frac{1}{2}P[y=0] + \frac{1}{2}P[y\neq0] \\ & = \frac{1}{2}P[y=0] + \frac{1}{2}(1 -P[y=0]) \\ & \le \frac{1}{2} \end{align}\)

In [7]:

SEED = 0
np.random.seed(seed=SEED)
random.seed(SEED)

num_exp = 10
t1, t2 = [0] * num_exp, [0] * num_exp
sizes = list(np.linspace(start=1, stop=500, num=num_exp))
for i, size in enumerate(sizes):
    size = int(size)
    a = np.random.randint(0, 100, size=(size, size)).tolist()
    b = np.random.randint(0, 100, size=(size, size)).tolist()
    # select ground truth as True or False equally likely.
    if random.random() <= 0.5:
        c = np.matmul(a, b).tolist()
        gt = True
    else:
        c = np.random.randint(0, 100, size=(size, size)).tolist()
        gt = False
    ans1, t1[i] = naive(a, b, c)
    ans2, t2[i] = check(a, b, c, k=2) # P[error] <= 2^{-k}
    # print("size={}, ground truth={}".format(size, gt))
    printProgressBar(iteration=i+1, total=num_exp, msg='experiments ...', length=50)
    assert gt == ans1 == ans2, "not correct!, where size={}, gt={}, ans1={}, ans2={}".format(size, gt, ans1, ans2)

|██████████████████████████████████████████████████| 100.0 % - experiments ...

In [8]:

plt.xlabel('size')
plt.ylabel('time')
plt.title("Time Complexity Analysis")
plt.plot(sizes, t1, 'o-g', label="naive")
plt.plot(sizes, t2, '*-r', label='frevald')
plt.legend(loc='upper left')
plt.show()

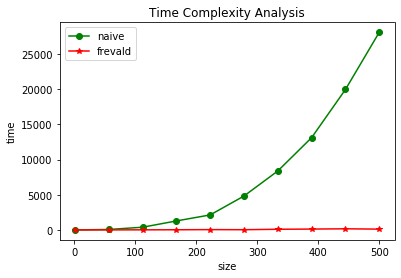
Report

Freivalds 알고리즘은 두개의 매트릭스와 그 결과 값으로 예상되는 매트릭스가 주어졌을때, 정말 그 결과가 두 매트릭스의 multiplication인지 check 하고자하는 determinisitic problem을 빠른 수행시간에 해결할 수 있다.
naive한 방식으로 계산을 하면 $O(n^3)$ 이 걸리며, divide and conquer 방식을 사용하는 strassen’s matrix multiplication algorithm은 $O( n^{log_2{7}}$ ) 수행시간이 걸린다.
하지만, strassen’s algorithm은 overhead가 큰 단점이 있다.

단순히 martrix의 multiplication결과가 일치하는지만 알고자하는 deterministic한 문제의 경우, Freivalds 알고리즘은 k 번의 iteration을 통해 error bound 를 $2^{-k}$까지 낮출 수 있어 매우 효과적이다. 하지만 주의해야할 점은 k의 선택을 잘해야한다는 점이다.

처음에 geeksforgeeks에서 random.random() % 2 이 부분이 0 또는 1로 output 하지 않아서, 구현하는데 실수가 있었다.

Reference

[1] wikiwand - Frevald
[2] geeksforgeeks