Climing the Leaderboard - hackerrank

In [1]:

#!/bin/python3
import sys
import numpy as np
import random, math
import logging, argparse, yaml, copy
import matplotlib.pyplot as plt
from utils.verbose import logging_time, printProgressBar
from collections import deque

In [2]:

toy_examples = \
"""7
100 100 50 40 40 20 10
4
5 25 50 120"""
msg = toy_examples
with open('input.txt', 'w') as f:
    f.write(msg)
    
toy_examples

'7\n100 100 50 40 40 20 10\n4\n5 25 50 120'

Climbing the Leaderboard

hackerrank

Given scores, user’s scores, find ordered statistic array for each time step.

Note that

1. given scores array is decreasing order.
2. given scores array of a user is increasing order.

It means a rank of a score does not affect each other.
Therefore, it is not necessarily to update scores.
e.g.,

scores = [100, 90, 70, 50]
alice = 30, 60, 102
30  is 5-th order.
60  is 4-th order, which is lesser than previous rank 5. 
102  is 1-th order, which is lesser than previous rank 4.

Also, when we find an order, only unique number is needed.

Key Idea

1. At first, we need to make scores array to be distinct numbers. This is because we can easily find ordered statistics.
2. Find each order from the distinct number, and then append it to ans.

Linear Search

I used linear seach for the first approach.
Time complexity is as follows.
\(O(nm)\)

In [3]:

# Complete the climbingLeaderboard function below.
@logging_time
def solve1(scores, alice):
    def linear(scores, x):
        """
        1. find index, assume that scores are sorted by decreasing order.
        2. insert x at right position.
        3. update scores.
        4. return ordered statistic. """
        for i in range(len(scores)):
            if x >= scores[i]:
                if x > scores[i]:
                    scores = scores[:i] + [x] + scores[i:]
                return i + 1
        scores.append(x)
        return i + 2
    
    # make distinct 
    new_scores = [scores[0]]
    for s in scores:
        if s != new_scores[-1]:
            new_scores.append(s)
    scores = new_scores

    ans = []
    for x in alice:
        ans.append(linear(scores, x))
    return ans

In [4]:

if __name__ == '__main__':
    # fptr = open(os.environ['OUTPUT_PATH'], 'w')
    sys.stdin = open('input.txt')

    n = int(sys.stdin.readline())
    scores = list(map(int, sys.stdin.readline().split()))
    m = int(sys.stdin.readline())
    alice = list(map(int, sys.stdin.readline().split()))

    result = solve1(scores, alice)
    print(result)

([6, 4, 2, 1], 0.008344650268554688)

However, it is too slow.

How can this algorithm be faster?

At first, it is not necessarily to change scores array. This is because given alice’s scores is ascending order. As I mentioned before, a rank of a score does not affect each other.

we only find within front range more and more. Also, we don’t need to update scores array.

Binary Search

Secondly, I used binary search approach. It takes

\[O(mlogn)\]

Please note that we should use binary search carefully!
This is because there are few exception we have to control in order to solve this problem.

Exceptions are as follows.

• the number x is not exist in scores.
  • The first and the last order are explicitly handled.
  • if x is no way to be found from binary search recursion, s > e case happend!

      if s > e:
          for i in range(e, s + 1):
              if scores[i] < x:
                  break
          return i + 1
    

  These code lines were hard to think for me.

In [5]:

@logging_time
def solve2(scores, alice):
    def bs(scores, s, e, x):
        # exceptions
        if scores[0] < x:
            return 1
        if scores[-1] > x:
            return len(scores) + 1
        if s > e:
            for i in range(e, s + 1):
                if scores[i] < x:
                    break
            return i + 1
        # base case
        elif s == e and scores[s] == x:
            return s + 1

        mid = (s + e) // 2
        if scores[mid] < x:
            return bs(scores, s, mid - 1, x)
        elif scores[mid] == x:
            return mid + 1
        else:
            return bs(scores, mid + 1, e, x)

    new_scores = [scores[0]]
    for s in scores:
        if s != new_scores[-1]:
            new_scores.append(s)
    scores = new_scores

    ans = []
    last = len(scores) - 1
    for x in alice:
        if ans != [] and (0 <= ans[-1] <= len(scores)-1): 
            last = ans[-1]
        ans.append(bs(scores, 0, last, x))
    return ans

In [6]:

if __name__ == '__main__':
    # fptr = open(os.environ['OUTPUT_PATH'], 'w')
    sys.stdin = open('input.txt')

    n = int(sys.stdin.readline())
    scores = list(map(int, sys.stdin.readline().split()))
    m = int(sys.stdin.readline())
    alice = list(map(int, sys.stdin.readline().split()))

    result = solve2(scores, alice)
    print(result)

([6, 4, 2, 1], 0.009775161743164062)

Therefore, I could pass all test.

Analysis

To generate data simply, let n = m.

In [7]:

num_seed = 1
num_exp = 100
step, num_step = 1, num_seed*num_exp
seeds = [random.randint(0, 100) for _ in range(num_seed)]
for j, SEED in enumerate(seeds):
    random.seed(SEED)
    np.random.seed(SEED)
    t1 = [[0]*num_exp for _ in range(num_seed)]
    t2 = [[0]*num_exp for _ in range(num_seed)]
    sizes = np.linspace(start=100, stop=10000, num=num_exp)
    for i, size in enumerate(sizes):
        size = int(size)
        scores = sorted(list(np.random.randint(0, size*10, size)), reverse=True)
        user = sorted(list(np.random.randint(0, size*10, size)))
        ans1, t1[j][i] = solve1(scores, user)
        ans2, t2[j][i] = solve1(scores, user)
        assert ans1 == ans2
        printProgressBar(iteration=step, total=num_step, msg="experiment...", length=50)
        step += 1 

|██████████████████████████████████████████████████| 100.0 % - experiment...

In [8]:

f, ax = plt.subplots(1,1)
colors = ['steelblue', 'peru', 'olivedrab', 'firebrick', 'darkolivegreen', 'darkblue', 'teal','coral',
              'lightblue', 'lime', 'orange','darkgreen', 'lavender', 'tan', 'salmon', 'gold','darkred',
              'turquoise','blue', 'green', 'red', 'cyan', 'magenta', 'yellow', 'black', 'purple', 'pink']
    
for i,j,k in zip(range(num_seed),t1,t2): 
    plt.plot(sizes, j, color=colors[i] , label='linear_{}'.format(i))
    plt.plot(sizes, k, color=colors[i+8], label='binary search_{}'.format(i))
    
plt.xlabel('size')
plt.ylabel('time')
plt.title("Time Complexity Analysis")
plt.legend(loc='upper left')
plt.show()

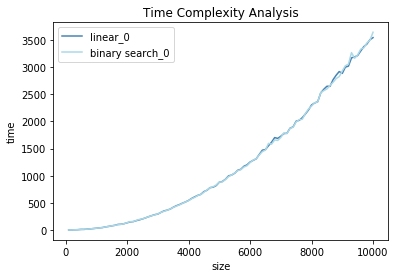
Report

먼저 unique한 array를 만들고, linear search를 생각하는데 까지는 쉽게 성공했다. 그러나, binary search를 하는 과정에서 exception 처리하는 부분이 나에게는 처리하는데 힘들었고, 마침내 성공했다.

binary search 를 연습하기에 아주 좋은 문제였다. offical한 binary search code 는 이 링크에 따로 적어두었다.