1
2
3
4
5
6
7
8
9
10
11
12
import networkx as nx
import numpy as np
import matplotlib.pyplot as plt
from collections import deque
from IPython.display import HTML
from matplotlib.animation import FuncAnimation
import copy
%matplotlib inline
Toy example
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
G = nx.DiGraph()
G.add_nodes_from(["w{}".format(i) for i in range(16)])
G.add_edges_from([('w{}'.format(i),'w{}'.format(i+1)) for i in range(0,5)])
G.add_edges_from([('w{}'.format(i),'w{}'.format(i+1)) for i in range(6,10)])
G.add_edges_from([('w{}'.format(i),'w{}'.format(i+1)) for i in range(11,15)])
G.add_edges_from([('w0','w6'),('w0','w11'),
('w1','w7'),('w2','w8'),('w6','w2'),('w7','w3'),('w8','w4'),
('w6','w12'),('w7','w13'),('w11','w7'),('w12','w8')])
pos = {'w0':[0,0], 'w6':[0,1], 'w7':[0,2], 'w8':[0,3], 'w9':[0,4], 'w10':[0,5],
'w1':[1,1], 'w2':[1,2], 'w3':[1,3], 'w4':[2,4], 'w5':[3,5],
'w11':[-1,1], 'w12':[-1,2], 'w13':[-1,3], 'w14':[-2,4], 'w15':[-3,5]}
labels = {'w{}'.format(i) : 'w{}'.format(i) for i in range(16)}
plt.figure(figsize=(10, 6))
nx.draw_networkx_nodes(G, pos, node_size=300, alpha=0.8, node_shape='o', node_color='red', label=pos.keys())
nx.draw_networkx_edges(G, pos, width=3, alpha=0.8, edge_color='blue')
nx.draw_networkx_labels(G,pos,labels,font_size=16)
plt.show()
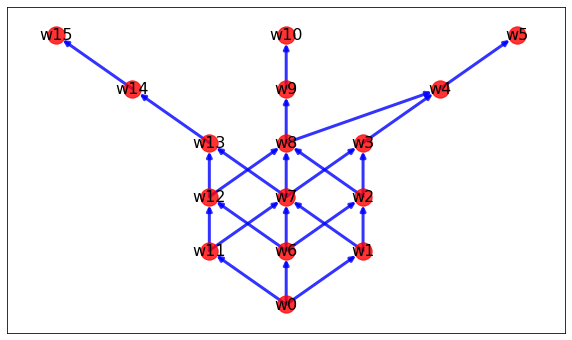
목표
아래와 같은 trajectory를 뽑아내는 것을 목표로 하자.
1
2
3
4
5
6
7
8
9
10
11
12
Go = nx.DiGraph()
Go.add_nodes_from(["w{}".format(i) for i in range(16)])
Go.add_edges_from([('w{}'.format(i),'w{}'.format(i+1)) for i in range(0,5)])
Go.add_edges_from([('w{}'.format(i),'w{}'.format(i+1)) for i in range(6,10)])
Go.add_edges_from([('w{}'.format(i),'w{}'.format(i+1)) for i in range(11,15)])
Go.add_edges_from([('w0','w6'),('w0','w11')])
plt.figure(figsize=(10, 6))
nx.draw_networkx_nodes(Go, pos, node_size=300, alpha=0.8, node_shape='o', node_color='red', label=pos.keys())
nx.draw_networkx_edges(Go, pos, width=3, alpha=0.8, edge_color='blue')
nx.draw_networkx_labels(Go, pos,labels,font_size=16)
plt.show()
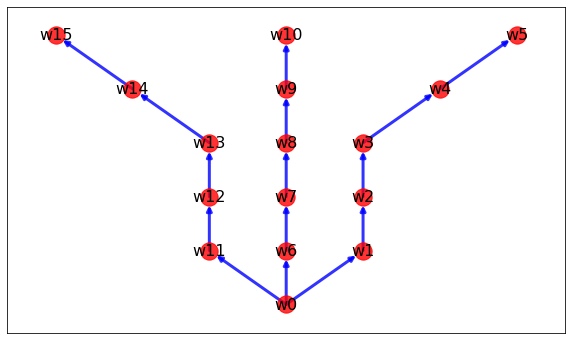
문제상황
그냥 dfs를 했을 때 back edge로 인한 싸이클 때문에 제대로 search가 불가능
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def dfs(G,i, max_depth=6):
ans = []
seen = {}
path = [i]
stack = [(i, 0, path)]
edges = []
while stack:
k, depth, path = stack.pop()
if depth == max_depth:
continue
seen[k] = True
print("visit node[{}], depth={}, path = {}".format(k, depth, path))
if depth == max_depth - 1:
ans.append(path)
print(ans)
for j in G.adj[k]:
if j not in seen:
edges.append((k,j))
path_ = copy.deepcopy(path)
if depth < max_depth - 1:
path_.append(j)
stack.append((j, depth+1, path_))
return edges, ans
edges, path = dfs(G,'w0')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
visit node[w0], depth=0, path = ['w0']
visit node[w11], depth=1, path = ['w0', 'w11']
visit node[w7], depth=2, path = ['w0', 'w11', 'w7']
visit node[w13], depth=3, path = ['w0', 'w11', 'w7', 'w13']
visit node[w14], depth=4, path = ['w0', 'w11', 'w7', 'w13', 'w14']
visit node[w15], depth=5, path = ['w0', 'w11', 'w7', 'w13', 'w14', 'w15']
[['w0', 'w11', 'w7', 'w13', 'w14', 'w15']]
visit node[w3], depth=3, path = ['w0', 'w11', 'w7', 'w3']
visit node[w4], depth=4, path = ['w0', 'w11', 'w7', 'w3', 'w4']
visit node[w5], depth=5, path = ['w0', 'w11', 'w7', 'w3', 'w4', 'w5']
[['w0', 'w11', 'w7', 'w13', 'w14', 'w15'], ['w0', 'w11', 'w7', 'w3', 'w4', 'w5']]
visit node[w8], depth=3, path = ['w0', 'w11', 'w7', 'w8']
visit node[w9], depth=4, path = ['w0', 'w11', 'w7', 'w8', 'w9']
visit node[w10], depth=5, path = ['w0', 'w11', 'w7', 'w8', 'w9', 'w10']
[['w0', 'w11', 'w7', 'w13', 'w14', 'w15'], ['w0', 'w11', 'w7', 'w3', 'w4', 'w5'], ['w0', 'w11', 'w7', 'w8', 'w9', 'w10']]
visit node[w12], depth=2, path = ['w0', 'w11', 'w12']
visit node[w6], depth=1, path = ['w0', 'w6']
visit node[w2], depth=2, path = ['w0', 'w6', 'w2']
visit node[w1], depth=1, path = ['w0', 'w1']
1
2
3
4
5
6
7
8
print(edges)
Ans = nx.DiGraph()
Ans.add_edges_from(edges)
plt.figure(figsize=(10, 6))
nx.draw_networkx_nodes(Ans, pos, node_size=300, alpha=0.8, node_shape='o', node_color='red', label=pos.keys())
nx.draw_networkx_edges(Ans, pos, width=3, alpha=0.8, edge_color='blue')
nx.draw_networkx_labels(Ans,pos,labels,font_size=16)
plt.show()
1
2
[('w0', 'w1'), ('w0', 'w6'), ('w0', 'w11'), ('w11', 'w12'), ('w11', 'w7'), ('w7', 'w8'), ('w7', 'w3'), ('w7', 'w13'), ('w13', 'w14'), ('w14', 'w15'), ('w3', 'w4'), ('w4', 'w5'), ('w8', 'w9'), ('w9', 'w10'), ('w6', 'w2')]
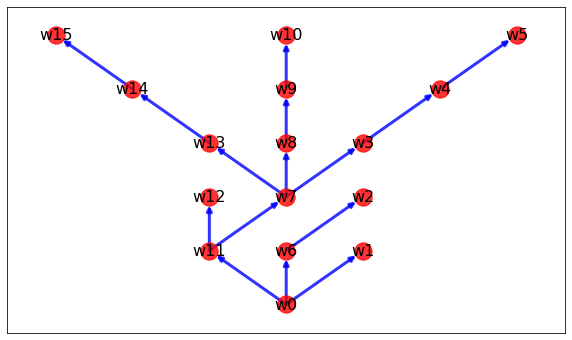
1
2
3
4
5
print(path)
Ans = nx.DiGraph()
for p in path:
nx.add_path(Ans, p)
nx.draw_networkx(Ans, pos=pos, with_label=True)
1
2
[['w0', 'w11', 'w7', 'w13', 'w14', 'w15'], ['w0', 'w11', 'w7', 'w3', 'w4', 'w5'], ['w0', 'w11', 'w7', 'w8', 'w9', 'w10']]
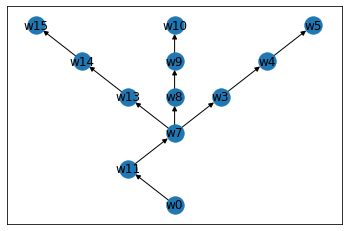
IDEA
그래프에서 시작점에서 멀어질수록 edge마다 weight를 부여하고,
그래프에서 w0를 start 로 하고 w15, w10, w5 까지 가는
최단 경로를 찾으면 된다.
간선의 가중치가 음이 아닌 일반적인 경우이고,
single source shortest path를 찾는 경우이므로 다익스트라 알고리즘을 사용하면 된다.
거리에 따라 weight부여
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
G_new = nx.DiGraph()
G_new.add_nodes_from(["w{}".format(i) for i in range(16)])
G_new.add_weighted_edges_from([('w{}'.format(i),'w{}'.format(i+1),1) for i in range(1,5)])
G_new.add_weighted_edges_from([('w{}'.format(i),'w{}'.format(i+1),1) for i in range(6,10)])
G_new.add_weighted_edges_from([('w{}'.format(i),'w{}'.format(i+1),1) for i in range(11,15)])
G_new.add_weighted_edges_from([('w0','w6',1),('w0','w1',1.5), ('w0','w11',1.5),
('w1','w7',2),('w2','w8',2),('w6','w2',2),('w7','w3',2),('w8','w4',2),
('w6','w12',2),('w7','w13',2),('w11','w7',2),('w12','w8',2)])
pos = {'w0':[0,0], 'w6':[0,1], 'w7':[0,2], 'w8':[0,3], 'w9':[0,4], 'w10':[0,5],
'w1':[1,1], 'w2':[1,2], 'w3':[1,3], 'w4':[2,4], 'w5':[3,5],
'w11':[-1,1], 'w12':[-1,2], 'w13':[-1,3], 'w14':[-2,4], 'w15':[-3,5]}
labels = {'w{}'.format(i) : 'w{}'.format(i) for i in range(16)}
plt.figure(figsize=(10, 6))
nx.draw_networkx_nodes(G_new, pos, node_size=300, alpha=0.8, node_shape='o', node_color='red', label=pos.keys())
nx.draw_networkx_edges(G_new, pos, width=3, alpha=0.8, edge_color='blue')
nx.draw_networkx_labels(G_new,pos,labels,font_size=16)
weight_labels = nx.get_edge_attributes(G_new,'weight')
nx.draw_networkx_edge_labels(G_new,pos,edge_labels=weight_labels)
plt.show()
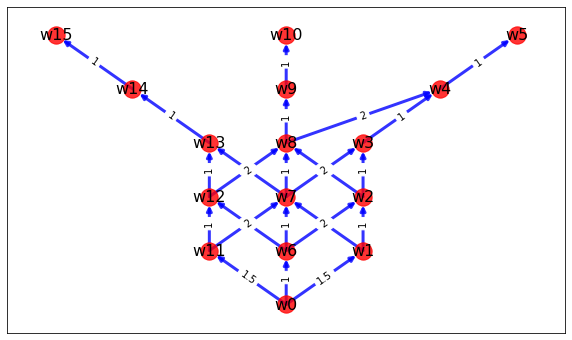
다익스트라를 이용한 search
우선순위 큐가 구현된 모듈인 heapq를 사용해서 구현하겠다.
heapq 모듈 사용법 참조1
heapq 모듈 사용법 참조2
조심해야 할점은 Q의 key로 참조하는 부분이 tuple의 맨앞이라는 점이다.
그리고 Queue를 업데이트 할때 heapq 모듈사용하면
새로운 힙을 만들고 다시 하나씩 push하도록 동작한다. 즉 build heap이기 때문에 O(n)가 소요된다.
하지만 새로운 heap을 만들지 않고 그 구조차체를 변경하는 경우 O(log(n)) 이 소요된다.
그렇게 하기 위해서는 아래의 두가지를 고려해야 한다.
- 변경할 key의 index를 log n 시간안에 찾기.
- heapify를 log n 시간안에 하기.
첫번째는 변경할 위치의 key를 업데이트 하기 위해서 그 index를 찾아야한다.
hash table을 사용해서 노드의 key를 갖고있고 그것을 계속 업데이트 해주면된다.
두번째는 값을 올리는 경우 위로 heapify하고 값을 내리는 경우 아래로 heapify한다.
1
import heapq
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
def Dijstra(Graph,r):
S = []
Q = []
D = {}
P = {}
for u in Graph.nodes:
if u == r:
D[u] = 0
else:
D[u]= float('inf')
P[u] = None
heapq.heappush(Q, (D[u], u))
while len(Q) != 0:
u = heapq.heappop(Q)[1] # O(VlgV)
print(" >> ", u, " vertex 꺼냄")
# 결정이 완료
S.append(u)
# relaxation을 통해 v.d 를 update 한다.(queue의 값 역시 update 필요)
# for each vertex v ∈ G.adj[u]
for v in list(Graph.adj[u]):
if (v not in S) and (D[u]+Graph[u][v]['weight'] < D[v]):
D[v] = D[u] + Graph[u][v]['weight']
# queue update
idx = 0
for i,q in enumerate(Q):
if q[1] == v:
idx = i
Q[idx] = (D[v], v)
heapq.heapify(Q)
P[v] = u
print(" >> Q's size: ", len(Q))
print("shortest path가 결정된 vertices set : ", S)
print("shortest path가 결정된 vertices 개수 : ", len(S))
# running time : O(( |V| + |E| )lg|V| )
return P
P = Dijstra(G_new,'w0')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
>> w0 vertex 꺼냄
>> Q's size: 15
>> w6 vertex 꺼냄
>> Q's size: 14
>> w1 vertex 꺼냄
>> Q's size: 13
>> w11 vertex 꺼냄
>> Q's size: 12
>> w7 vertex 꺼냄
>> Q's size: 11
>> w12 vertex 꺼냄
>> Q's size: 10
>> w2 vertex 꺼냄
>> Q's size: 9
>> w8 vertex 꺼냄
>> Q's size: 8
>> w13 vertex 꺼냄
>> Q's size: 7
>> w3 vertex 꺼냄
>> Q's size: 6
>> w9 vertex 꺼냄
>> Q's size: 5
>> w14 vertex 꺼냄
>> Q's size: 4
>> w4 vertex 꺼냄
>> Q's size: 3
>> w10 vertex 꺼냄
>> Q's size: 2
>> w15 vertex 꺼냄
>> Q's size: 1
>> w5 vertex 꺼냄
>> Q's size: 0
shortest path가 결정된 vertices set : ['w0', 'w6', 'w1', 'w11', 'w7', 'w12', 'w2', 'w8', 'w13', 'w3', 'w9', 'w14', 'w4', 'w10', 'w15', 'w5']
shortest path가 결정된 vertices 개수 : 16
Find path
1
P
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
{'w0': None,
'w1': 'w0',
'w2': 'w1',
'w3': 'w2',
'w4': 'w3',
'w5': 'w4',
'w6': 'w0',
'w7': 'w6',
'w8': 'w7',
'w9': 'w8',
'w10': 'w9',
'w11': 'w0',
'w12': 'w11',
'w13': 'w12',
'w14': 'w13',
'w15': 'w14'}
1
2
3
4
5
6
7
8
9
10
11
12
paths =[]
for node in list(G_new.nodes):
path = []
parent = node
while True:
if parent is None:
break
path += [parent]
parent = P[parent]
path.reverse()
paths.append(path)
paths
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
[['w0'],
['w0', 'w1'],
['w0', 'w1', 'w2'],
['w0', 'w1', 'w2', 'w3'],
['w0', 'w1', 'w2', 'w3', 'w4'],
['w0', 'w1', 'w2', 'w3', 'w4', 'w5'],
['w0', 'w6'],
['w0', 'w6', 'w7'],
['w0', 'w6', 'w7', 'w8'],
['w0', 'w6', 'w7', 'w8', 'w9'],
['w0', 'w6', 'w7', 'w8', 'w9', 'w10'],
['w0', 'w11'],
['w0', 'w11', 'w12'],
['w0', 'w11', 'w12', 'w13'],
['w0', 'w11', 'w12', 'w13', 'w14'],
['w0', 'w11', 'w12', 'w13', 'w14', 'w15']]
1
2
3
4
5
6
7
8
9
Solution = nx.DiGraph()
for path in paths:
Solution.add_path(path)
plt.figure(figsize=(10, 6))
nx.draw_networkx_nodes(Solution, pos, node_size=300, alpha=0.8, node_shape='o', node_color='red', label=pos.keys())
nx.draw_networkx_edges(Solution, pos, width=3, alpha=0.8, edge_color='blue')
nx.draw_networkx_labels(Solution, pos,labels,font_size=16)
plt.show()
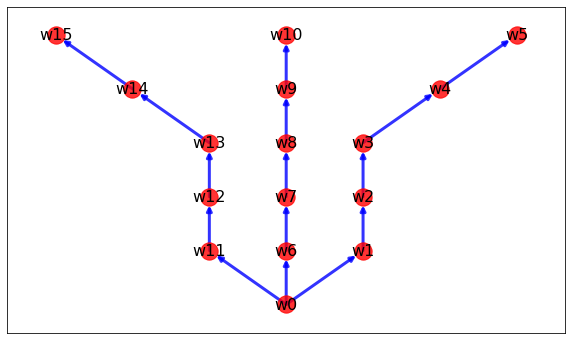
A star를 이용한 search
목적지가 정해져있고 하나의 path만 찾고싶다면
굳이 weight를 부여하고 할 필요없이 A star 알고리즘을 사용하면 된다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
class Node():
"""A node class for A* Pathfinding"""
def __init__(self, name, parent=None, position=None):
self.name = name
self.parent = parent
self.position = position
self.g = 0
self.h = 0
self.f = 0
# 연산자 오버로딩
def __eq__(self, other):
return self.position == other.position
def astar(G, pos, start, end):
"""Returns a list of tuples as a path from the given start to the given end in the given maze"""
# Create start and end node
start_node = Node(start, None, pos[start])
start_node.g = start_node.h = start_node.f = 0
end_node = Node(end, None, pos[end])
end_node.g = end_node.h = end_node.f = 0
# Initialize both open and closed list
open_list = [] # 탐색중인 Node가 담긴 container : heap자료구조이면 좋다. 근데 귀찮으니 그냥 list로..
closed_list = [] # path설정이 완료된 Node
# Add the start node
open_list.append(start_node)
# Loop until you find the end
while len(open_list) > 0:
# Get the current node
current_node = open_list[0]
current_index = 0
# openlist에 들어있는 Node 들 중 가장작은 f값을 갖는 Node를 꺼내온다.
for index, item in enumerate(open_list):
if item.f < current_node.f:
current_node = item
current_index = index
# Pop current off open list, add to closed list
open_list.pop(current_index)
closed_list.append(current_node)
# Found the goal
# Node 백트랙캉하면서 위치좌표를 path에 넣고 마지막에 path에 들어간 순서를 뒤집어서 순서대로 해줌
if current_node == end_node:
path = []
current = current_node
while current is not None:
path.append(current.name)
current = current.parent
return path[::-1] # Return reversed path
# Generate children
# children은 인접하고 길이될 수 있는 노드들의 list이다.
children = []
for new_name in list(G.adj[current_node.name]): # Adjacent squares
# Get node position 인접한 노드의 위치
node_position = pos[new_name]
# Create new node
new_node = Node(new_name, current_node, node_position)
# Append
children.append(new_node)
# Loop through children
for child in children:
# Child is on the closed list
# 경로설정이 완료된 노드는 통과
finished = False
for closed_child in closed_list:
if child == closed_child:
finished = True
if finished:
continue
# Create the f, g, and h values
child.g = current_node.g + 1
child.h = math.sqrt(((child.position[0] - end_node.position[0]) ** 2)
+ ((child.position[1] - end_node.position[1]) ** 2))
child.f = child.g + child.h
# Child is already in the open list
# 인접한 노드들 중 탐색 중인 노드를 이전 값과 비교하여 g값이 update가 필요하다면 update
# 이미 탐색중이므로 중복되서 open_list 에 들어갈 필요 없으니 continue로 넘김
is_exist = False
index = 0
for open_node in open_list:
if child == open_node:
is_exist =True
index = i
if is_exist:
if child.g > open_list[index].g:
continue
# update open list
open_list.pop(index)
# Add the child to the open list
open_list.append(child)
path1 = astar(G,pos, 'w0', 'w15')
path2 = astar(G,pos, 'w0', 'w10')
path3 = astar(G,pos, 'w0', 'w5')
paths = []
paths.append(path1)
paths.append(path2)
paths.append(path3)
1
paths
1
2
3
[['w0', 'w11', 'w12', 'w13', 'w14', 'w15'],
['w0', 'w6', 'w7', 'w8', 'w9', 'w10'],
['w0', 'w1', 'w2', 'w3', 'w4', 'w5']]
1
2
3
4
5
6
7
8
9
AstarSolution = nx.DiGraph()
for path in paths:
AstarSolution.add_path(path)
plt.figure(figsize=(10, 6))
nx.draw_networkx_nodes(AstarSolution, pos, node_size=300, alpha=0.8, node_shape='o', node_color='red', label=pos.keys())
nx.draw_networkx_edges(AstarSolution, pos, width=3, alpha=0.8, edge_color='blue')
nx.draw_networkx_labels(AstarSolution, pos,labels,font_size=16)
plt.show()
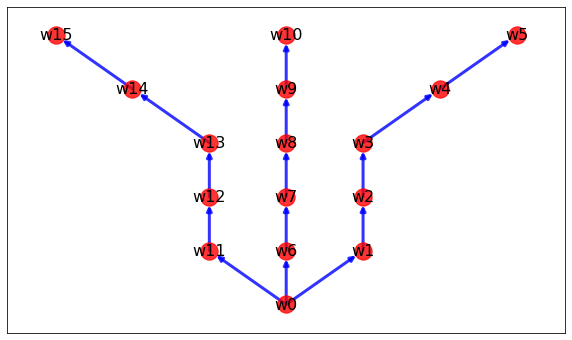


Leave a comment