Dattn [RecSys’17 review]

Dattn [Rec Sys’17]

Intro

attension mechanism (local attension, global attension) 적용.

local attension의 intuition: user’s preferences, item’s properties 에 대한 insight 제공.

detail: CNN layer로 들어가기 전에 review정보의 local window에서 유용한 keyword를 선택하는 일.

global attension 의 intuition: 전체 review text의 semantic 한 의미를 파악.

detail: 긴 review 정보로 부터 noisy하고 irrelevant한 word들을 골라냄.

이 논문에서는 review에 대한 feature들을 끄집어기위해 CNN을 사용하는데, user review와 item review를 함께 input으로 넣으면 각 user에 대한 review의 feature와 item에 대한 review feature를 따로 파악하기 힘들기 때문에 각각 독립된 neural net을 만들고, aggregate하는 작업을 한다. 따라서, user reivew와 item review에서 각각 CNN 을 거치면 user에 대해서, item에 대해서 각각 semantic meaning을 파악할 수 있다.

Convention 방법들의 한계점

• CF
  • cold start problem. 즉, records(주어진 rating 값)이 부족할 경우, reliable 하지 않다.
  • popular한 item만 계속 추천될 수 있다.
  • content정보를 무시한다.
• text를 이용한 방법들
  • ratings meet reviews, RMR 모델: item의 review로 부터 topic을 찾고 이를 이용한 model. 한계점: 각각의 user의 sentimental 한 expression 을 cover하지는 않는다. 예를 들면, ‘nice’라는 단어를 review에서 사용하는 user A, B 가있을때, A는 rating을 5점 주었지만, B는 rating을 4점을 주었다면, B에게는 nice가 rating에 무조껀 좋은것은 아니다. (즉, user들의 review를 분석해 보면, 각 user별로 고유한 preference를 파악 가능하다.)

Contribution

• CNN에 들어가기전 interpretable한 attension을 적용
• Dual attension 구조 사용
• 성능 우위

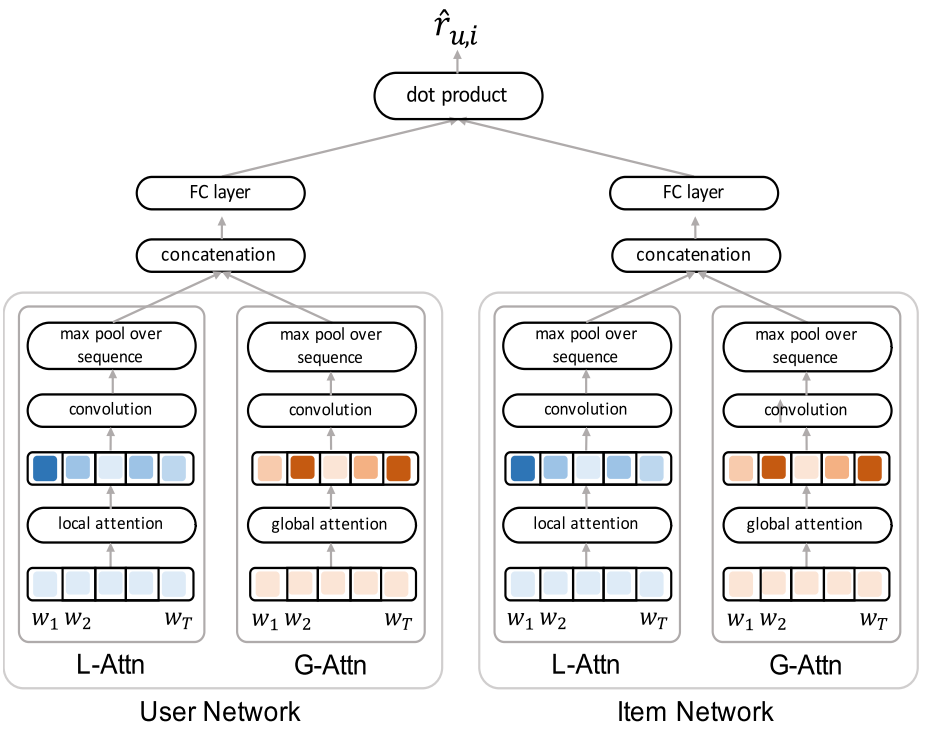
Proposed Model

L-Attn: local attension, Gttn: global attension

$D_u $: user documents, $D_i$ item documents

Embedding layer

$\mathcal{V}$ : set of words

$\mathbf{e_t} \in \mathbb{R}^{\lvert \mathcal{V} \rvert}$ : a onehot vector for a word

$\mathbf{x_t} \in \mathbb R^d$ : embedded vector for a word, $d$ : embedding dimension

$ \mathbf{W_e} \in \mathbb{R}^{d \times | \mathcal{V} |}$ : embedding weights \(\mathbf{x_t} = \mathbf{W_e} \mathbf{e_t}\) Document 가 주어졌을때, 그안의 word를 embedding 하는 과정.

($t$번째 word인 $word_t$의 onehot vector $ \mathbf{e_t}$를 기준으로 수식은 위와 같이 됨.)

$ \mathbf{W_e} $ 의 값은 pretrained 된 값을 가져다가 사용할 수 있다.(DeepCoNN, NARRE에서 그렇게 했음.)

L-Attn

$\color{red}{ \bigstar \text{ index noation이 헷갈려서 조금 변경하였다.}}$

user Network를 기준으로 설명하면,

$\mathbf{T}$ 개의 words 로 이루어진 $ D_u $가 있을 때 $\mathbf {W_e}$를 통해 embedding 하면, $(\mathbf{x_1, …, x_T})$를 얻는다.

어떤 word( $t$번째 word)를 중심으로 attension window 안에 있는 local attension score $s(t)$, $t =1, ..,\mathbf{T}$ 값을 얻고, 이를 바탕으로 attension값이 반영된 embedding vector $ \mathbf{ \hat{x_t^L}} \in \mathbb{R^d}$ , $t = 1, .., \mathbf T$를 계산한다.

이때, sliding window size $w$ 에 대해 local attension silding kernel $\mathbf{W_{l-att}^1} \in \mathbb{R^{w \times d}} $ 이고, $t$번째 word 가 중심에 있는 silding window 에 해당 되는 word에 대한 embedding vectors $\mathbf{X_{l-att,t}} \in \mathbb{R^{w \times d}} $ 이라 하면 다음과 같이 계산 (여기서, $\mathbf{ *}$는 element wise product, $g(.) = sigmoid(.)$ ) $\color{red}{\text{ (중심이 딱 안맞는 경우는 어떻게 할지는 NARRE 참고하겠다.) }}$ \(\mathbf{X_{l-att,t} = (x_{t+ \frac{-w+1}{2}}, x_{t+ \frac{-w+3}{2}}, .., x_t, ..., x_{t+ \frac{w-1}{2}})^T} \\ s(t) = g(\mathbf{X_{l-att,t} * W_{l-att}^1 + b_{l-att}^1}), ~~~~~~ t\in [1,T] \\ \mathbf{\hat{x_t^L}} = s(t)\mathbf{x_t} ~~~~ \color{green}{\text{# attension이 걸린 embedding vector}}\) 위에서 구해진 local attension이 걸린 embedded word vector이 CNN의 input으로 들어가게 된다.

local attension 부분의 CNN 에서의 kernel 은 size가 1인데, 그 이유는 user의 preference 또는 propery keywords에 를 반영하기 위해서 이다.(즉, 개별적인 word별 feature를 뽑아냄)

따라서, word에 대한 index $t $, kernel에 대한 index $j$ 라 하고, kernel의 수를 $ n_{l-att}$라고 할때,

kernel $\mathbf{W_{l-att}^2} \in \mathbb{R^{ d \times n_{l-att}}}$ 를 이용하여 convolution을 하면 $\mathbf{Z_{l-att}}(t= .. , j=..) \in \mathbb{R^{\mathbf{T} \times n_{l-att}}}$ 를 얻고, 각 word 에 대해서 $ \mathbb{R^{ \mathbf{T} \times d }}$ dimension을 가진 kernel로 max pooling 하면, 각 knerel 별로 scalar 값 $\mathbf{z_{l-att}}(j) \in \mathbb{R}, j = 1,.., n_{l-att}$를 얻을 수 있다.

(여기서, $g(.) = tanh(.)$ , $\mathbf{Z_{l-att}}(t,j) \in \mathbb{R}$ ) \(\mathbf{Z_{l-att}}(t,j) = g(\mathbf{\hat{x}_t^L * W_{l-att}^1}(:,j) + \mathbf{b_{l-att}^1}(j)), ~~~j \in [1,n_{l-att}] ~~~~ \color{green}{ \text{# convolution} }\\ \mathbf{z_{l-att}}(j) = \underset{ 1\le t \le \mathbf{T}}{\operatorname{Max}}( \mathbf{Z_{l-att}}(t=..,j)) ~~~~ \color{green}{ \text{# max pooling} }\)

G-Attn

global attension 이 걸린 embedding은 각 word에 대한 score $s(t)$를 구할때, attension window가 자기 자신이 된다. 그렇게 구한 attensioned embedding vector들을 $ \mathbf{\hat{x}{_{t}^{G}}} , \forall t$ 라 하고, CNN의 input이 된다. $\color{red}{\text{ ( local은 가운데를 중심으로 했는데 global은 어떻게 계산하는지는 확실히 아직 모르겠음, NARRE를 참고 해보겠다.) }}$

CNN 에서는 local 때와 다르게, kernel size $w_f$ 를 갖게 되며, (이렇게 하는 이유는, 단어들 사이의 관계를 고려한 feature를 추출해 내기 위함인것 같다.) kernel의 수를 $n_{g-att}$ 이라하자. 그렇게 kernel $\mathbf{W_{g-att}} \in \mathbb{R^{ w_f \times d \times n_{g-att}}}$ 로 convolution을 하고, L-attn 때와 동일한 방식으로 $ \mathbb{R^{ (\mathbf{T}-w_f+1) \times d }}$dimension을 가진 kernel로 max pooling을 하면, 각 knerel 별로 scalar 값 $\mathbf{z_{g-att}}(j) \in \mathbb{R}, j = 1,.., n_{g-att}$를 얻을 수 있다.

(여기서, $g(.) = tanh(.)$ , $\mathbf{Z_{g-att}}(i,j) \in \mathbb{R}$ ) \(\mathbf{\hat{X}_{g-att,i} = (\hat{x}_{i}^G, \hat{x}_{i+1}^G, .., \hat{x}_{i+w_f-1}^G)^T}, ~i\in [1,\mathbf{T}-w_f+1] ~ \color{green}{\text{# attensioned embedding vectors }}\\ \mathbf{Z_{g-att}}(i,j) = g(\mathbf{\hat{X}_{g-att,i}^G * W_{g-att}}(:,:,j) + \mathbf{b_{g-att}}(j)), ~~~j \in [1,n_{g-att}] ~~~~ \color{green}{\text{# convolution}} \\ \mathbf{z_{g-att}}(j) = \underset{ 1\le i \le (\mathbf{T}-w_f+1)}{\operatorname{Max}}( \mathbf{Z_{g-att}}(i=..,j)) ~~~~ \color{green}{ \text{# max pooling} }\)

위의 수식은 kernel size = $w_f$ 에 대해서만 convolution을 하였는데, 여러 kernel size를 사용할 수 있다. ex., $[w_f^1, w_f^2, .., w_f^{n_w}]$. 따라서, kernel size의 갯수를 $n_w$ 로 하겠다.

FC layer

L-Attn 의 output과 G-attn의 outputs 를 concatenation하여 FC의 input으로 만든다. 그리고, FC layer에서 2개의 Affline layer를 사용하여 dimension을 축소시켜 user, item에 대한 latent vector 를 얻는다.

FC layer에서 layer size = $[500,50]$으로 가정하면,
\(\mathbf{W}_{FC}^1 \in \mathbb{R}^{500 \times (n_{l-att} + n_w \times n_{g-att})} \\ \mathbf{W}_{FC}^2 \in \mathbb{R}^{50 \times 500}\)

$\oplus$는 concatenation 연산, \(\mathbf{z}_{out}^1 \in \mathbb{R}^{n_{l-att} + n_w \times n_{g-att}} \\ $g(.) = ReLu(.)\)

\[\mathbf{z}_{out}^1 = \mathbf{z}_{l-att} \oplus \mathbf{z}_{g-att}^1 \oplus ... \oplus \mathbf{z}_{g-att}^{n_w} ~~ \color{green}{\text{# flattened}} \\ \mathbf{z}_{out}^2 = g(\mathbf{W}_{FC}^1\mathbf{z}_{out}^1 + \mathbf{b}_{FC}^1) \\ \gamma_u = g(\mathbf{W}_{FC}^2\mathbf{z}_{out}^2 + \mathbf{b}_{FC}^2)\]

Training

estimated rating 값은 user NN part와 item NN part를 inner product 함으로써 얻는다. 이러한 접근은 각 user에 대한 latent vector값과 item에 대한 latnet vector 값에 대해서 MF(Matrix Factorizaion) 방법을 사용한 것이다. \(\hat{r}_{u,i} = \gamma_u^T \gamma_i\) Attension layer의 weights, CNN layer의 kneral weights, FC layer의 weights 를 learn하기 위해서는 위의 estimated rating 값이 정확해 질수 있도록 하는 objective function이 필요하다.

그 loss function은 MSE를 이용하여 learning 한다.

$N $ = rating값을 알고있는 entry의 갯수 \(L = \frac{1}{N}\sum_{(u,i)}{(r_{u,i} - \hat{r}_{u,i} )^2}\)

Experiments

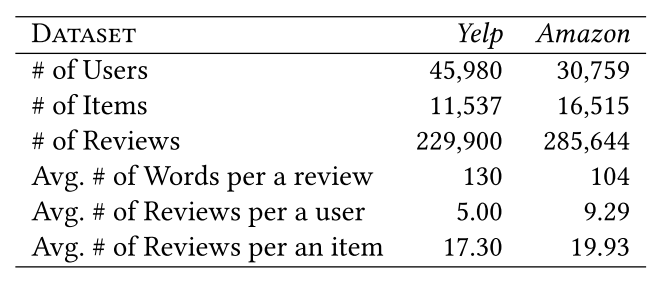
Dataset의 Statistic

Yelp[^1], Amazon[^2] dataset에 대한 statistic

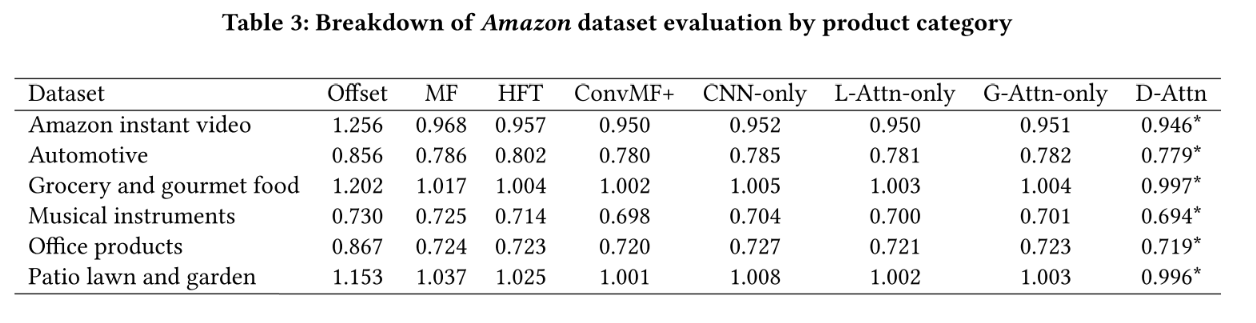
성능 표, 다른 모델들과의 비교