RRT star

RRT*

지난 절에 이어서 RRT*에 대해서

알고리즘을 알아보고

코딩과 결과를 분석해보자.

RRT*는 RRT를 개선하여 optimal path를 찾게 하도록 개선한 알고리즘이다.

*의 의미는 optimal의 의미를 담고 있다.

어떤 부분을 변경했는지 알아보자.

Pseudo Code

차이가 있는 부분은 두가지 이다.

기본적으로 path의 길이를 고려하여 cost를 만들고 tree를 만들게 된다.

확장된 노드의 부모를 거리를 고려하여 바꾸는 것 Chooseparent와

기존의 노드들을 부모를 거리를 고려하여 바꾸는 것 Rewire Tree 가 추가되었다.

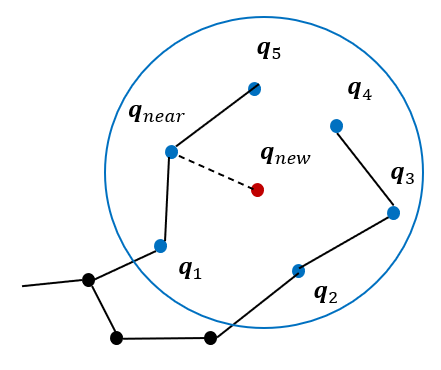
새로 추가된 노드 근방의 여러 노드 중

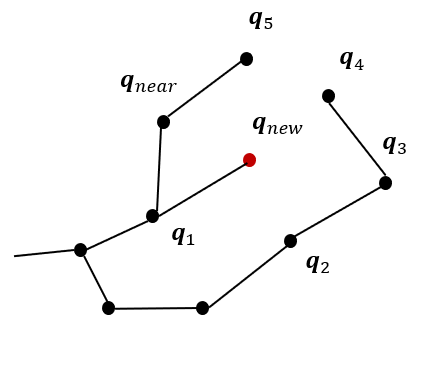
루트에서 부터의 거리를 고려하여 가장 가까운 노드를 찾고 그것을 부모노드로 설정한다.

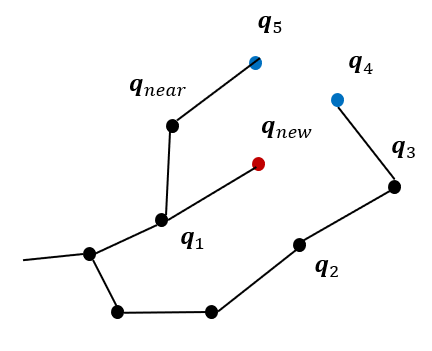
또한 주변 노드들 중에서 새로운 노드를 부모로 바꾸었을 때 cost가 줄어든다면

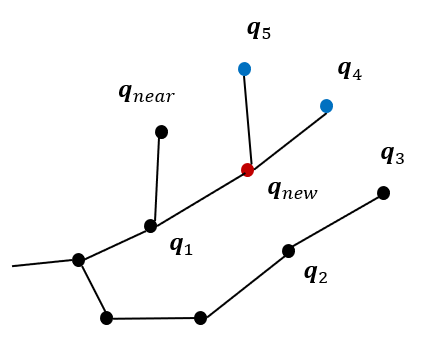
그 노드들의 부모를 바꾸어 Tree를 rewiring한다.

코드

아래 부분이 RRT*의 핵심 계획부분이다.

def plan(self):
        """Plans the path from start to goal while avoiding obstacles"""
        self.node_list = [self.start]
        for i in range(self.max_iter):
            # Create a random node inside the bounded environment
            rnd = self.get_random_node()
            # Find nearest node
            nearest_node = self.get_nearest_node(self.node_list, rnd)
            # Get new node by connecting rnd_node and nearest_node
            new_node = self.steer(nearest_node, rnd, self.max_extend_length)
            # If path between new_node and nearest node is not in collision:
            if not self.collision(new_node, nearest_node, self.obstacle_list):
                near_inds = self.near_nodes_inds(new_node)
                # Connect the new node to the best parent in near_inds
                new_node = self.choose_parent(new_node, near_inds)
                self.node_list.append(new_node)
                # Rewire the nodes in the proximity of new_node if it improves their costs
                self.rewire(new_node, near_inds)
        last_index, min_cost = self.best_goal_node_index()
        if last_index:
            return self.final_path(last_index), min_cost
        return None, min_cost

다른 부분은 RRT와 같고 choose_parent, rewire, new_cost 부분의 함수만 자세히 살펴보자.

new_cost는 다음과 같이 시점부터 종점까지 거리에 따른 비용을 계산한다.

    def new_cost(self, from_node, to_node):
        """to_node's new cost if from_node were the parent"""
        d = np.linalg.norm(from_node.p - to_node.p)
        return from_node.cost + d

부모의 비용에 현재의 노드까지 거리가 더해져서 비용함수를 계산한다.

choose parent 함수로 들어가보자.

	def choose_parent(self, new_node, near_inds):
        """Set new_node.parent to the lowest resulting cost parent in near_inds and
        new_node.cost to the corresponding minimal cost
        """
        min_cost = np.inf
        best_near_node = None
        # modify here: Go through all near nodes and evaluate them as potential parent nodes by        
        if not near_inds:
            return None            
        for i in near_inds:          
          # 1) checking whether a connection would result in a collision,
          near_node = self.node_list[i]                    

          # 2) evaluating the cost of the new_node if it had that near node as a parent,
          new_cost = np.inf if self.collision(new_node, near_node, self.obstacle_list) else self.new_cost(near_node, new_node)     

          # 3) picking the parent resulting in the lowest cost and updating
          #    the cost of the new_node to the minimum cost.
          if min_cost > new_cost:
            min_cost = new_cost
            best_near_node = near_node          

        if min_cost == np.inf:
          print("There is no good path.(min_cost is inf)")
          return None

        # Don't need to modify beyond here
        new_node.cost = min_cost
        new_node.parent = best_near_node
        return new_node

새로운 노드의 주변 노드들 중에서 edge를 만들었을 때 collision없고

cost가 최소가 되는 노드로 부모를 바꾸게 된다.

이어서 rewire함수로 들어가보자.

	def rewire(self, new_node, near_inds):
        """Rewire near nodes to new_node if this will result in a lower cost"""
        # modify here: Go through all near nodes and check whether rewiring them
        # to the new_node would:                         
        for i in near_inds:
          near_node = self.node_list[i]     

          # A) Not cause a collision and
          not_collision = not self.collision(new_node, near_node, self.obstacle_list)          

          # B) reduce their own cost.
          new_cost = self.new_cost(new_node, near_node)
          improved_cost = near_node.cost > new_cost

          # If A and B are true, update the cost and parent properties of the node.
          if not_collision and improved_cost:        
            near_node.cost = new_cost
            near_node.parent = new_node
            
            # Don't need to modify beyond here
            self.propagate_cost_to_leaves(new_node)

새로운 노드의 주변 노드들의 부모를 새로운 노드로 바꾸었을 때

충돌이 생기지 않고 cost가 개선된다면 부모를 새로운 노드로 바꾼다.

	def propagate_cost_to_leaves(self, parent_node):
        """Recursively update the cost of the nodes"""
        for node in self.node_list:
            if node.parent == parent_node:
                node.cost = self.new_cost(parent_node, node)
                self.propagate_cost_to_leaves(node)

이후 새로운 노드에 subtree가 추가 되었기 때문에

그 subtree 들의 leaf 노드들까지 cost를 reculsive하게 업데이트해 주어야한다.

결과

RRT*를 통해 생성된 결과는 다음과 같다.

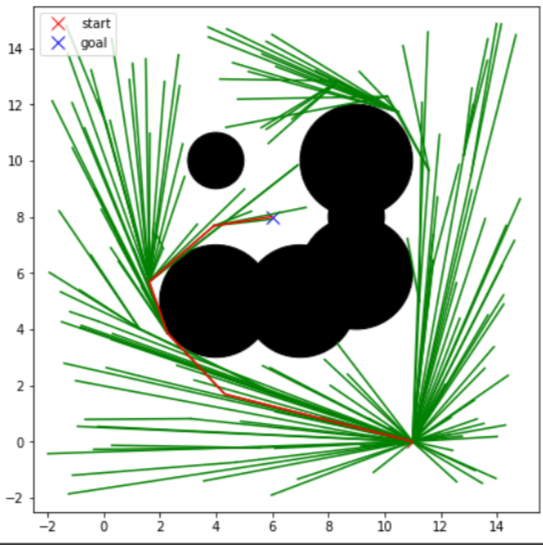
Span된 Tree는 RRT와 달리 Fan shaped Structure를 갖게 되고

이러한 특징이 목표지점까지 optimal path를 그리도록 만든다.

고찰

최적 경로를 생성하는 문제는 해결했지만

고차원이고 Search space가 넓을 경우 샘플링 영역에 대한 이슈는 여전하다.

그리고 이동체의 운동역학을 고려하지 않은점,

dynamic한 장애물이 있을 경우의 문제점등을 여러가지 이슈가 있다.

랜덤 샘플들을 통해서 목표까지 도달해야 하기 때문에

탐색과 활용(exploration and exploitation)의 균형이라는 문제를 안고 있다.

샘플링에 대한 이슈는 균일하게 샘플을 만드는 것이 아니고

일정 목적에 따라서 편향된 샘플링 전략을 만들면 위 문제를 다룰 수 있다고 한다.

지능 샘플링(intelligent sampling), 두 단계 샘플링(two-stage sampling), 포텐셜 필드(potential field) 방법들이 존재한다고 한다.

하지만 편향된 샘플링을 하면 목표까지 빠르게 경로를 생성할 수 있지만 형상공간 전체를 탐색하지 못해서

최적 경로를 만들지 못할 수도 있는 문제가 있다.

Reference

RRT설명 블로그

RRT Colab코드

Pseudo Code

RRT와 RRT* 비교 블로그