Word2Vec Algorithm
Word2Vec [1] 는 단어를 벡터로 나타내는 방법 이다.
단어를 어떻게 벡터로 나타내기 위해 가정상황이 필요하다.
Word2Vec에서는 동일 문맥에 등장하는 단어는 비슷한 의미를 지닌다는 distributional hypothesis에 근거하여 단어를 벡터 표현으로 바꾼다.
이때의 Word2Vec가 가정하는 핵심사항은 다음과 같다.
- 동일 문맥을 특정 중심단어를 기준으로 일정 크기의 윈도우 안의 주변 단어로 생각 $\Rightarrow$ 동일 문맥(특정 윈도우)안에 자주 등장한다면 비슷한 단어
- 비슷한 의미를 지닌 두 단어, 즉 중심단어에 대한 벡터 표현과 주변 단어에 대한 벡터 표현 사이 내적값이 크도록 학습 $\Rightarrow$ softmax 함수를 통해 중심단어로 주변단어 예측 혹은 주변단어로 중심단어 예측
따라서, 다음과 같은 과정을 통해 위의 가정상황을 반영한 단어 벡터 표현을 찾는다.
- 자연어로 구성된 Corpus가 주어지면 일정크기의 윈도우를 슬라이딩 해가며 중심단어와 그 주변단어 데이터 셋을 구성한다.
- 그 데이터 셋에 대해 동일 문맥에 등장하는 중심단어와 주변단어를 벡터 표현으로 바꾸고 그 벡터 표현 사이의 내적값이 커지도록 하는 예측 모델을 학습한다.
예측모델은 앞서 말했듯 두 가지의 예측 모델을 구성할 수 있다.
- 중심단어로 주변단어를 예측 - Skip Gram 모델
- 주변단어로 중심단어 예측 - Continuous Bag Of Words (CBOW) 모델
각 모델의 Architecture 는 다음과 같다.
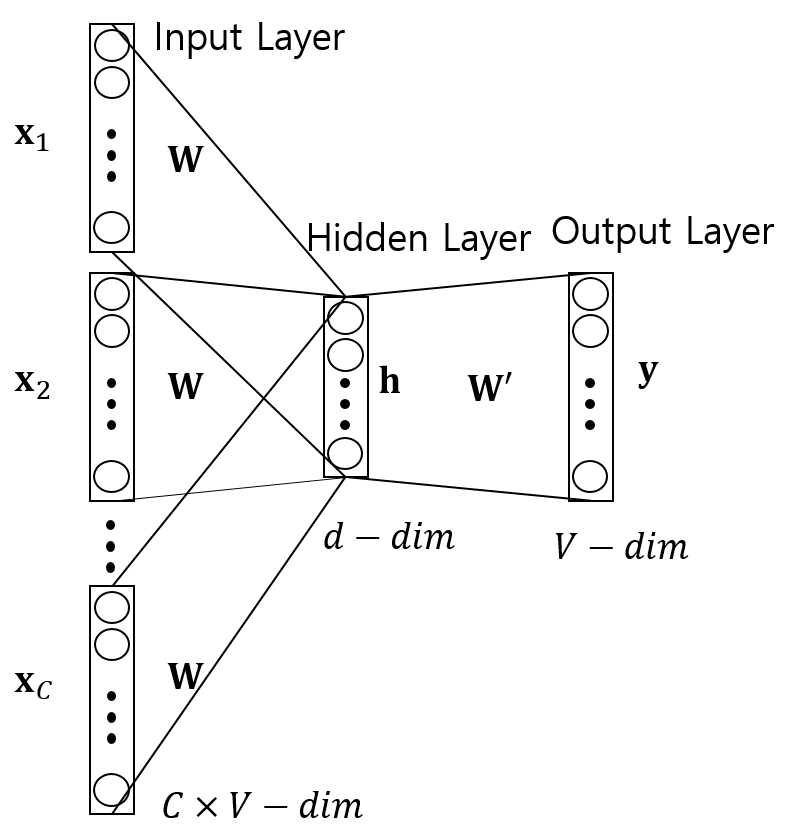

동일 문맥을 특정 중심단어를 기준으로 일정 크기의 윈도우 안의 주변 단어 이다.
동일 문맥안의 중심단어는 하나씩만 존재한다는 사실을 주목하자.

Training Instance #1:
[Target (natural)], [Context (language, processing)]
[list([1, 0, 0, 0, 0, 0, 0, 0, 0]), list([[0, 1, 0, 0, 0, 0, 0, 0, 0], [0, 0, 1, 0, 0, 0, 0, 0, 0]])]
위의 그림과 같이 Training Instance를 만들때,
CBOW 모델처럼 주변단어로 중심단어를 예측하는 경우는 하나의 문맥에 하나의 Training Instance 밖에 만들지 못한다.
반면, Skip-Gram 모델처럼 중심단어로 주변단어를 에측하도록 하면 하나의 문맥에서 여러 Training Instance 들을 만들 수 있다.
따라서, Skip-Gram의 경우에 하나의 문맥 정보로부터 그 중심단어는 여러번의(주변단어 수 만큼) 업데이트 기회를 갖게 된다.
이러한 차이점 때문에 이 Article 에서 다음과 같이 특성을 주장하고 있다.
| CBOW | Skip-Gram |
|---|---|
| 주변단어로 중심단어 예측 | 중심단어로 주변단어 예측 |
| 적은양의 단어 corpus로 많은양의 Training Instance 생성 | 동일 Corpus에 대해 Skip-Gram모다 학습량이 적음 |
| Corpus안의 적은 빈도 수의 단어도 벡터표현으로 잘 학습됨 | 자주 등장하는 단어에 대해 잘 학습됨 |
전체적인 performance는 Skip-Gram 방식이 더 좋은 것으로 알려져 있다.
수식적인 설명
CBOW 와 Skip-Gram 둘중 Skip-Gram에 집중하여 설명하겠다.

수식적 설명에 앞서 Notation을 정리하면 다음과 같다.
| 수식 표현 | 의미 | <div style="width:100px">Shape</div> | <div style="width:150px">조건</div> |
|---|---|---|---|
| $V$ | Corpus안의 전체 단어 수 | 1 | - |
| $C$ | 동일 문맥안의 주변 단어 수 | 1 | - |
| $d$ | 임베딩된 단어 벡터 차원 | 1 | - |
| $x$ | 중심단어 | $1$ | one-hot 인코딩된 벡터 $\mathbf{x}$, where shape$=V$ |
| $t_{c}$ | 주변단어 | $1$ | one-hot 인코딩된 벡터 $\mathbf{t}_c$, where shape$=V$ and $c \in [1, C]$ |
| $\mathbf{y}_{c}$ | 주변단어의 logit | $V$ | $c \in [1, C]$ |
| $\mathbf{W}$ | 중심단어 임베딩 행렬 | $V \times d$ | - |
| $\mathbf{W}^{\boldsymbol{‘}}$ | 주변단어 임베딩 행렬 | $d \times V$ | - |
| $\mathbf{h}$ | 중심단어의 은닉층 표현 | $d$ | - |
Skip-Gram의 신경망 네트워크에서 $\mathbf{W}$는 각 단어를 벡터 표현으로 변환하는 Embedding Matrix를 의미한다.
예를 들면 Corpus 내에 존재하는 중심단어 $x$는 one-hot 인코딩되어 $\mathbf{x}$가 되고, 다음의 과정을 거쳐 은닉층의 단어의미가 집약된 벡터표현 $\mathbf{h}$를 얻을 수 있다.
\(\mathbf{h} = \mathbf{W} \mathbf{x}\)
그 후, 중심단어 $x$에 대한 $c=1, 2, …, C$ 번째 주변단어에 대한 logit $\mathbf{y}_{c}$를 다음과 같이 얻는다. \(\mathbf{y}_{c} = \mathbf{W}^{\boldsymbol{'}T}\mathbf{h}, \forall c \in [1, C]\)
이때, Word2Vec에서 주장하는 학습 원리는 다음과 같다.
중심단어에 대한 의미가 집약된 벡터표현 ($\mathbf{h}=\mathbf{W}\mathbf{x}$ 즉, $\mathbf{W}$의 $x$에 대응되는 행벡터)와
$c$번째 주변단어에 대한 의미가 집약된
벡터표현 $ \mathbf{t}_c \odot \mathbf{W}^{\boldsymbol{‘}T}$즉, $\mathbf{W}^{‘^T}$의 $t_c$에 대응되는 행 벡터, where $c\in [1, C]$)
사이의 내적 값인 유사도 \(\mathbf{y}_{c, t_c} = (\mathbf{t}_c \odot \mathbf{W}^{\boldsymbol{'}T}) \odot (\mathbf{W} \mathbf{x}) = \mathbf{t}_c \mathbf{W}^{\boldsymbol{'}T} \odot \mathbf{W} \mathbf{x} = \mathbf{t}_c \mathbf{W}^{\boldsymbol{'}T} \mathbf{h}\) ( $\mathbf{y}_{c, t_c}$ 는 $\mathbf{y_c}$ 에서 주변단어 $t_c$ 에 대응되는 원소)가 크도록 학습하는 것이 목표이다.
다음과 같이 softmax 함수를 이용하면 중심단어 $x$에 대한 $c$번째 주변단어에 대한 logit $\mathbf{y}_{c}$을 $V$개의 단어들에 대한 확률 값에 대한 예측 벡터가 된다. \(\begin{bmatrix} P(\mathbf{y}_{c, 1} \mid x) \\ P(\mathbf{y}_{c, 2} \mid x) \\ ... \\ P(\mathbf{y}_{c, V} \mid x) \end{bmatrix} = softmax(\mathbf{y}_c)\)
이때, 다음 그림과 같이
$\mathbf{y}_{c}$ 에서 $t_{c}$에 대응하는 원소 값 $\mathbf{y}_{c, t_c} \in [0, 1], \text{scalar}$이 크도록
$\mathbf{W}, \mathbf{W}^{\boldsymbol{‘}}$를 학습하는 것이($\because \mathbf{y}_{c} = \mathbf{W}^{‘T} \mathbf{W} \mathbf{x}$) 목표이다. \(\begin{bmatrix} P(\mathbf{y}_{c, 1} \mid x) \\ P(\mathbf{y}_{c, 2} \mid x) \\ ... \\ \color{red}{P(\mathbf{y}_{c, t_c} \mid x) \uparrow } \\ ... \\ P(\mathbf{y}_{c, V} \mid x) \end{bmatrix}\)
위의 목표를 달성하기 위해 cross entropy를 줄이도록 모델의 weights 값들 $\mathbf{W}, \mathbf{W}^{\boldsymbol{‘}}$를 학습한다.
\[\text{cross_entropy}(\mathbf{t}_c, \mathbf{y}_c) = -\mathbf{t}_c \odot log(softmax({\mathbf{y}_c}))\]정리하면 다음과 같이 수식으로 나타낼 수 있다. \(\begin{align} \underset{\mathbf{W}, \mathbf{W}^{'}}{\text{maximize }} P(\mathbf{y}_{1, t_1}, \mathbf{y}_{1, t_2}, ..., \mathbf{y}_{1, t_C} \mid x; \mathbf{W}, \mathbf{W}^{'}) \\ P(\mathbf{y}_{1, t_1}, \mathbf{y}_{1, t_2}, ..., \mathbf{y}_{C, t_C} \mid x) &= \Pi_{c=1}^C {P(\mathbf{y}_{c, t_c} \mid x)} \text{ suppose that } y_{1, t_1}, ..., y_{C, t_C} \text{ are independent each other} \\ P(\mathbf{y}_{c, t_c} \mid x) &= \mathbf{t}_c \odot softmax({\mathbf{y}_c}) \\ &= \frac{exp(\mathbf{y}_{c, t_c})}{\sum_{j=1}^V {exp(\mathbf{y}_{c, j})}} \\ &= \frac{exp(\mathbf{t}_c \mathbf{W}^{\boldsymbol{'}T} \odot \mathbf{W} \mathbf{x})}{\sum_{j=1}^V {exp(\mathbf{W}^{\boldsymbol{'}T}[j, :] \odot \mathbf{W} \mathbf{x})}} \\ &= \mathbf{t}_c \frac{exp( \mathbf{W}^{\boldsymbol{'}T} \odot \mathbf{W} \mathbf{x})}{\sum_{j=1}^V {exp(\mathbf{W}^{\boldsymbol{'}T}[j, :] \odot \mathbf{W} \mathbf{x})}} \\ \therefore \underset{\mathbf{W}, \mathbf{W}^{'}}{\text{maximize }} \Pi_{c=1}^C {P(\mathbf{y}_{c, t_c} \mid x)} \text{ suppose that } y_{1, t_1}, ..., y_{C, t_C} & \Longleftrightarrow \underset{\mathbf{W}, \mathbf{W}^{'}}{\text{minimize }} -\sum_{c=1}^C log {P(\mathbf{y}_{c, t_c} \mid x)} \\ -\sum_{c=1}^C log {P(\mathbf{y}_{c, t_c} \mid x)} &= -\sum_{c=1}^C log(\mathbf{t}_c \odot softmax({\mathbf{y}_c})) \\ &= -\sum_{c=1}^C \mathbf{t}_c \odot log(softmax({\mathbf{y}_c})) \\ &= \sum_{c=1}^C \text{cross_entropy}(\mathbf{t}_c, \mathbf{y}_c) \end{align}\)
따라서, $loss = \sum_{c=1}^C \text{cross_entropy}(\mathbf{t}_c, \mathbf{y}_c)$ 를 줄이는 방향으로 모델의 weights $\mathbf{W}, \mathbf{W}^{\boldsymbol{‘}}$를 학습한다.
Speed Up Training
$V$ 사이즈에 비례에 계산량이 늘기때문에 Word2Vec의 학습을 좀더 빠르게 하기위한 3가지 heuristics가 존재한다 [6].
[4]에 영어로 자세한 사항들이 적혀있고, 솔라리스의 인공지능 연구실에 한글로 자세히 번역되어 있다.
Subsampling Frequent words
그림 2를 보면 and, is와 같이 의미적으로 중요하지 않은 단어가 학습 데이터에 많이 포함되어있다는 사실에 주목하자.
이런 단어들은 자주 등장하므로 학습 시 update가 자주 되어 속도 저하를 유발한다.
따라서, 자주 등장하는 단어는 학습에서 제외시키도록 Subsampling 하는 방법이다.

단어 $v_i, i=1, 2,…, V$ 에 대해 학습 시 제외될 확률 $P(v_i)$을 $v_i$의 Frequency를 고려하여 다음과 같이 정의한다.($t$는 실험적으로 결정하는 하이퍼 파라미터로 [1]에서 $10^{-5}$를 사용하였다.) \(P(v_i) = 1 - \sqrt{\frac{t}{freq(v_i)}}\)
Negative Sampling
loss 를 계산하려면 중심단어에 대한 모든 단어 $V$ 중 주변단어를 예측하는 Softmax 함수를 다음과 같이 통과 해야한다.
\(\begin{align}
softmax({\mathbf{y}_c}) &= \frac{exp(\mathbf{y}_{c})}{\sum_{j=1}^V exp(\mathbf{y}_{c, j}) } \\
&= \begin{bmatrix}
P(\mathbf{y}_{c, 1} \mid x) \\ P(\mathbf{y}_{c, 2} \mid x) \\ ... \\ P(\mathbf{y}_{c, V} \mid x)
\end{bmatrix}
\end{align}\)
이때 분모의 연산은 $O(V)$이므로 $V$가 클 경우, 학습 속도를 저하시킨다.
이 방법은 모든 $V$에 대해서 Softmax를 취하는 게 아니라 일부만으로 계산하고자 하는 것이 목표이다.
context, 즉 중심단어를 기준으로 윈도우 안에 들어가 있는 단어들을 positive, 없는 단어를 nagtive로 정의하고,
negative 단어들 중 Frequency가 높은 단어를 우선적으로 고려하여 다음과 같은 확률(Unigram Distribution)로 뽑힌 샘플들을 뽑아 계산한다.
참고로 이 확률 값은 고정된 값이므로 preprocessing 단계에서 미리 계산해 놓는다.
(3/4 가 곱해진 이유는 frequency가 좀 낮은 경우에는 뽑힐 확률을 높히도록 완화시키는 역할)
\(P(v_i) = \frac{freq(v_i)^{3/4}}{\sum_{i=1}^V freq(v_i)^{3/4}}\)
따라서, loss 를 Softmax function 에 의한 cross entropy가 아니라
Sigmoid 함수를 이용하여
- postive 샘플에 대한 binary cross entropy와,
- negative 샘플에 대한 binary cross entropy를
합하는 방법을 사용한다.
결과적으로, 중심단어 $x$에 대한 loss 는 다음과 같이 구한다. \(\require{cancel} \require{color} \begin{align} loss &= \sum_{c=1}^C \begin{bmatrix} \textcolor{green}{\text{binary_cross_entropy}(t_c, y_{c, t_c})} &+& \textcolor{red}{\sum_{j \sim P(x)} \text{binary_cross_entropy}(t_j, y_{c, j})} \end{bmatrix} \\ &= \sum_{c=1}^{C} \begin{bmatrix} 1 \cdot log(sigmoid(\mathbf{y}_{c, t_c})) + \cancel{ (1 - 1) \cdot log(1 - sigmoid(\mathbf{y}_{c, t_c}))} &+& \sum_{j \sim P(x)} \cancel{0 \cdot log(sigmoid(\mathbf{y}_{c, j}))} + (1 - 0) \cdot log(1 - sigmoid(\mathbf{y}_{c, j})) \end{bmatrix} \\ &= \sum_{c=1}^{C} \begin{bmatrix} log(sigmoid(\mathbf{y}_{c, t_c})) &+& \sum_{j \sim P(x)} log(1 - sigmoid(\mathbf{y}_{c, j})) \end{bmatrix} \\ &= \sum_{c=1}^{C} \begin{bmatrix} log(sigmoid(\mathbf{y}_{c, t_c})) &+& \sum_{j \sim P(x)} log(sigmoid(- \mathbf{y}_{c, j})) \end{bmatrix} \text{, since } 1 - sigmoid(\mathbf{y}_{c, j}) = sigmoid(- \mathbf{y}_{c, j})\\ \end{align}\)
Hierachical Softmax
Negative Sampling 과 동일한 목표를 두고 있다.
Softmax 함수에서 분모의 연산은 $O(V)$이므로 $V$가 클 경우, 학습 속도를 저하시킨다는 단점을 개선하기 위해
$O(logV)$ 만큼의 단어만 고려하겠다는 아이디어이다.
다음 그림과 같이 각 단어를 leaves로 가지는 binary tree를 만들고,

</div>
root로 부터 해당 leaf로 가는 path에 따라 확률을 곱해나가는 random walk 확률을 구한다.
word2vec 논문에서는 이러한 Binary Tree로 Binary Huffman Tree를 사용했다고 한다.
(수식에 관한 Detail 설명은 빠뜨렸으므로 [4]혹은 [6]을 참고)
Hierachical Softmax방식과 Negative Sampling 은 양자택일로 사용된다.
Code Implementation
[5] pytorch NLP tutorial - 김성동님 참고하여 작성 예정…
Reference
[1] Word2Vec paper
[2] English blog
[3] korean blog
[4] Word2Vec learning details
[5] pytorch NLP tutorial - 김성동님
[6] Word2Vec speed up paper
[7] 한글 정리


Leave a comment