Hidden Markov Model Theory

HMM

Hidden Markov Models (HMM)은 직전 상태에만 영향받는다는 Markov chain 전제가 있다. HMM은 observable state와 관련성있는 hidden state 사이의 확률 관계들을 모델 파라미터로 갖는다. 이 모델 파라미터들이 주어진 observation들의 통계정보가 반영되도록 학습하여 이를 이용하는 모델이다. (여기서 상태는 random variable 값이다.)

observation sequence 로부터 hidden state와의 관계를 파악하는 unsupervised learning이 가능하다.

좀더 디테일한 설명

observation은 hidden state 조건에 상관없이 관찰가능한 상태 값을 의미. 내재적으로 observation은 hidden state 정보가 반영되어 관찰된다. 이 observation 값으로 계속 모델을 업데이트 하다보면 observation state와 hidden state사이의 관계가 학습됨을 이용한다. 즉, 학습 전에는 모델파라미터 값과 observation들의 관련도가 부정확하지만 수많은 관측치들로 업데이트가 많이 되면 될수록 정확해 진다.

왜 이 문제가 중요한가?

Observation들은 어떤 기록들을 의미하고, 이 기록들로부터 알고싶은 숨겨진 정보를 찾는 것이 가능하다. (숨겨진 정보의 정답 없이 학습 가능) 예를 들면, 아이스크림을 먹은 갯수 기록을 보고 숨겨진 날씨정보를 찾는다던지 단어 시퀀스(문장)에 숨겨진 품사 정보를 찾는데 이용할 수 있음.

점진적으로 학습해나가는 모델 파라미터 값들은 다음과 같다.

• Initial State Probability: hidden state가 발생할 확률.
• State Transition Probability: hidden state간의 transition 확률.

• Emission Probability: 어떤 시점에서 관측치들로 얻은 조건부 확률 p(observation state at a time step

  hidden state).

이렇게 세 종류의 probability들은 Beysian Network의 모델 파라미터를 의미하기 때문에 HMM은 Beysian Network의 일종이다.

이해하기 쉽도록 standford lecture: HMM를 한글로 정리해 놓은 ratsgo’s blog: HMM 를 먼저 보고 오자.

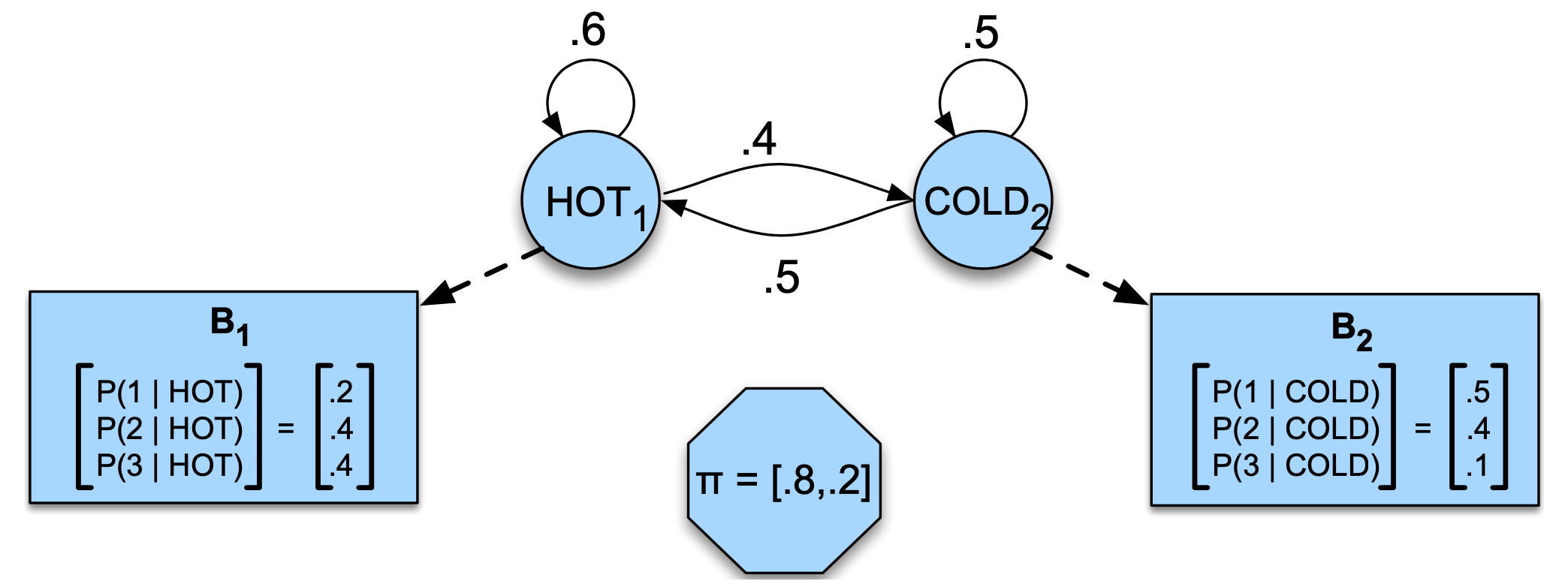
toy example로 모델이 이미 학습되었다는 가정하에 날씨와 아이스크림을 먹은 횟수에 대한 HMM model 파라미터는 다음 그림과 같다. 여기서 관측가능한 변수는 아이스크림을 먹은 횟수 (1, 2, 3) 만 가능.

Fig1. HMM 모델의 예

HMM를 이용하는 flow는 다음과 같다. 모델 파라미터(state transition probabilty, emission probability, start probabilty)는 임의의 초깃값으로 정한다. 이 값은 정확하지 않을 수 있다. 관측된 observation 값들 이용하여 likelihood를 구하고, 그 likelihood를 최대화하도록(EM 알고리즘 방식) 모델 파라미터들을 업데이트해나간다. 업데이트가 충분히 진행되었다면, observation 들의 통계정보가 모델 파라미터에 반영될 것이다.

모델 파라미터가 통계정보를 충분히 흡수하여 어느정도 수렴한다면 어떻게 이용될 수 있을까?

어떤 주어진 observation 시퀀스가 있을때 각 observation 마다 모델 파라미터의 state가 어떤 값이 되었을때 likelihood(그동안 쌓아온 통계정보에 얼마나 근접한가의 정도)가 최대가 되는지 알 수 있다.

즉, 관측 정보만 가지고 상태를 예측할 수 있다.

이 예제에서는 아이크림 먹은 갯수만 가지고 그날의 날씨를 예측하는 것이 가능해진다. 이 예제말고 사용되는 하나의 어플리케이션은 어떤 문장을 주었을때 그 문장의 형태소 마다 품사 태깅을 할 수 있다.

Train

likelihood를 최대화 하는 모델 파라미터를 최적화해야하는 데 변수가 많거나 관측할 수없는 변수가 있다면 최적화가 어렵다.

이때 파라미터를 학습하는 방법은 EM (혹은 Baum-Welch) algorithm 을 이용한다. 두 단계를 반복하며 진행된다.

Fig2. EM(Baum-Welch) Algorithm

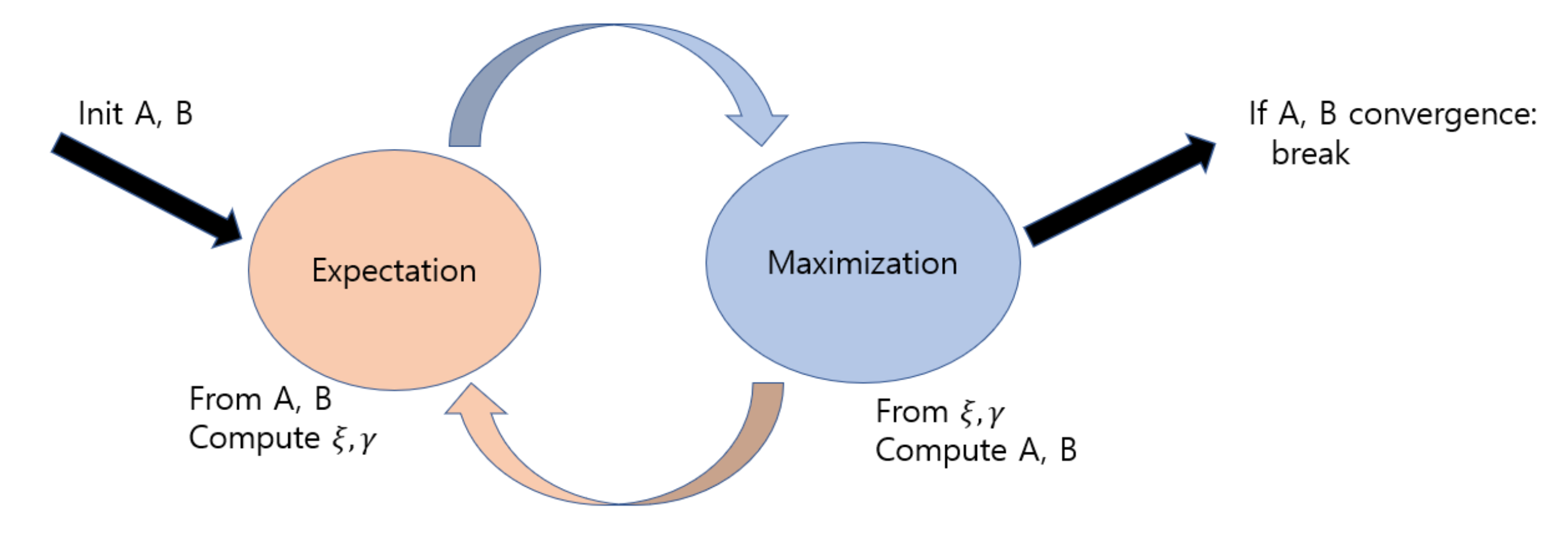
Fig3. Pseudo Code of Baum-Welch Algorithm

E-step

모델 파라미터를 바탕으로 observation state에 대한 joint log likelihood를 구한다.

맨 처음 step 에서는 추정해야하는 모델 파라미터값들을 초기화가 필요하다.

주어진 모델 파라미터에는 관측치에 대한 정보가 반영된 값이다. 현재 모델 파라미터 정보들을 바탕으로 주어진 관측치 값이 최대한 나올 수 있도록 하는 likelihood 를 찾는 것이 목표이다. (즉, upper bound를 찾는 과정이다.)

joint log likelihood를 구하는 과정에서 hidden state에 대한 observation probability 값을 marginalize 해야한다.

이때 joint log likelihood 값은 forward 혹은 backward 알고리즘을 통해 구한다. (효율적 계산을 위해 dynamic programming이 사용된다.)

observation sequecne 길이는 $T$ 이고, 상태 수는 $N$ 이라 하자.

naive 하게 계산하면 $O(T N^T)$ 이지만 dynamic programming을 쓰면 $O(N^2T)$ 에 빠르게 계산할 수 있다.

Fig4. Evaluation: Forward and Backward Algorithm

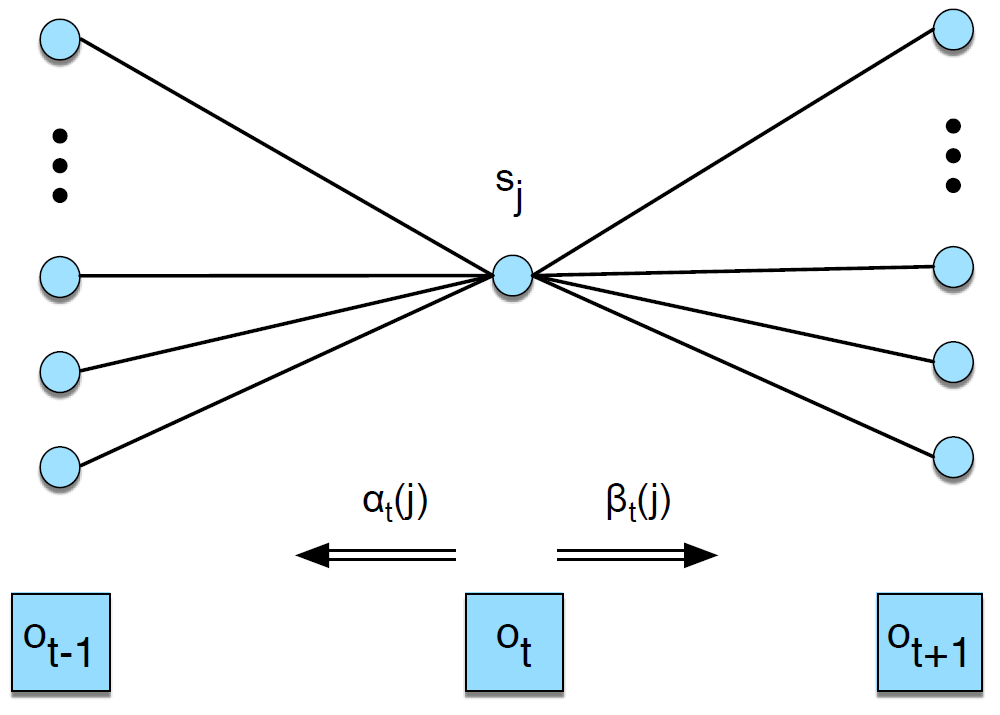
$\alpha, \beta$ 의 의미는 다음과 같다.

\[\begin{aligned} \alpha_t(j) &= P(o_1,o_2,…,o_t,q_t=j \vert \lambda) \\ \beta_t(j) &= P(o_{t+1},o_{t+2},…,o_T,q_t=j \vert \lambda) \end{aligned}\]

효율적 계산을 위해 dynamic programming을 다음과 같이 이용한다. \(\begin{aligned} {\alpha}_{t}(j) &=\sum_{i=1}^{n}{ {\alpha}_{t-1}(i)\times {a}_{ij} } \times {b}_{j}({o}_{t}) \\ {\beta }_{t}(i) &=\sum_{j=1}^{n} {a}_{ij} \times {b}_{j}({o}_{t+1}) \times {\beta}_{t+1}(j) \end{aligned}\)

forward 혹은 backward 알고리즘을 통해 $\alpha, \beta$ 값을 계산한다는것은 다음과 같이 likelihood를 계산한다는 의미이다.

\[\begin{aligned} P(O \vert \lambda ) =&P \left( {o}_{1}, {o}_{2}, ..., {o}_{T} \vert \lambda \right) \\ =&P \left( {o}_{1}, {o}_{2}, ..., {o}_{T}, {q}_{t}={q}_{F} \vert \lambda \right) ={\alpha}_{T} \left({q}_{F} \right) \end{aligned}\] \[\begin{aligned} P(O|\lambda )=&P\left( {o}_{1}, {o}_{2},...,{o}_{T} \vert \lambda \right) \\ =&P\left( {o}_{1}, {o}_{2}, ..., {o}_{T}, {q}_{t} = {q}_{0} \vert \lambda \right) = \beta_{0} \left( {q}_{0} \right) \\ =&\sum_{s=1}^{n}{\alpha_{t} \left( s \right) \times \beta_{t} \left( s \right)} \end{aligned}\]

이제 (주어진 관측 시퀀스와 현재 모델 파라미터에 대한 upper bound 값으로) likelihood를 구했으니, 이 값으로 모델 파라미터를 업데이트 하면 된다.

Question: 왜 likelihood는 upper bound 가 되는가? 잘 기억해보면 Dynamic programming 을 통해 최적의 likelihood를 forward/backword 알고리즘을 통해 구했다.

깔끔하게도 업데이트 하기 위해 필요한 중간 파라미터인 $\xi, \gamma$ 만 구해놓으면 나머지는 M-step 에서 사용되지 않아서 생각하지 않아도 된다.

$t$시점에 $i$번째 상태이고 $t+1$시점에 $j$번째 상태일 확률 $\xi_t(i, j)$ 는 다음과 같이 구한다.

Fig4. xi(크시) 업데이트

\[\begin{aligned} {\xi}_{t} \left( i,j \right) =&\frac { P \left( {q}_{t} = i, {q}_{t+1} = j, O \vert \lambda \right) }{ P\left( O \vert \lambda \right) } \\ =&\frac { {\alpha}_{t} \left( i \right) \times {a}_{ij} \times {b}_{j} \left( {o}_{t+1} \right) \times {\beta}_{t+1}\left( j \right) }{ \sum_{s=1}^{n}{ \alpha _{t}\left( s \right) \times \beta_{t} \left( s \right)} } \end{aligned}\]

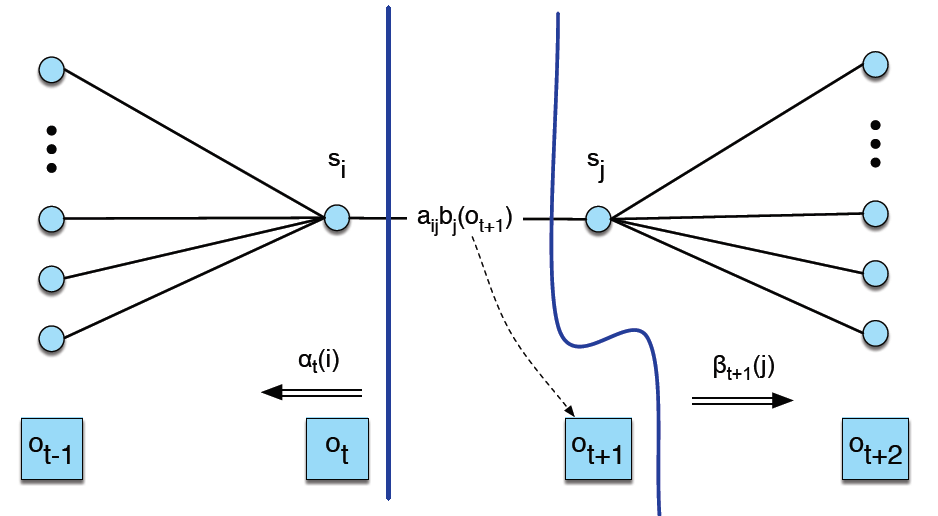
$t$시점에 $j$번째 상태일 확률 $\gamma_t(j)$ 는 다음과 같이 구한다. \(\begin{aligned} { \gamma }_{ t }\left( j \right) =&P \left( { q }_{ t }=j|O,\lambda \right) \\ =&\frac { P\left( { q }_{ t }=j,O|\lambda \right) }{ P\left( O|\lambda \right) } \\ =&\frac { { \alpha }_{ t }\left( j \right) \times { \beta }_{ t }\left( j \right) }{ \sum _{ s=1 }^{ n }{ \alpha _{ t }\left( s \right) \times \beta _{ t }\left( s \right) } } \end{aligned}\)

---

위에서 다음의 베이즈 정리가 자주 사용되니 기억해 놓자. \(\begin{aligned} P\left( X|Y,Z \right) &= \frac { P(X,Y,Z) }{ P(Y,Z) } \\ &= \frac { P(X,Y)/P(Z) }{ P(Y,Z)/P(Z) } \\ =&\frac { P(X,Y|Z) }{ P(Y|Z) } \end{aligned}\)

M-step

E-step에서 구한 likelihood가 반영된 중간 변수 $\xi, \gamma$ 를 이용하여 모델파라미터 값들을 업데이트(추정) 한다.

$i$번째 상태에서 $j$번째 상태로 전이할 확률 $\hat{a}_{ij}$. \(\hat { a } _{ ij }=\frac { \sum _{ t=1 }^{ T-1 }{ { \xi }_{ t }\left( i,j \right) } }{ \sum _{ t=1 }^{ T-1 }{ \sum _{ k=1 }^{ N }{ { \xi }_{ t }\left( i,k \right) } } }\)

$a_{ij}$은 $t$에 대한 $\xi_t(i,j)$의 기댓값을 의미하므로 위와 같이 계산된다. 어떤 시점이든 $i$번째 상태에서 다른 상태로 전이할 확률 $\xi_t$가 존재하므로 관측치 시퀀스 전체에 걸쳐 모든 시점에 대해 $\xi_t$를 더해주는 것이다. 다만 분모와 분자 모두에 $\sum_{t=1}^{T-1}$가 적용된 이유는 시퀀스 마지막 $T$번째 시점에선 종료상태로 전이될 확률이 $1$이 되므로 $t$에 대해 $1$에서 $T−1$까지 더해줌. 또 주목할점은 $\gamma_{t}(i) = \sum_{k=1}^{N} \xi_{t}(i, k)$ 이다.

$j$번째 상태에서 관측치 $v_k$가 방출될 확률 $\hat{b}_{j}(v_k)$. \({ \hat { b } }_{ j }\left( { v }_{ k } \right) =\frac { \sum _{ t=1,s.t.{ o }_{ t }={ v }_{ k } }^{ T }{ { \gamma }_{ t }\left( j \right) } }{ \sum _{ t=1 }^{ T }{ { \gamma }_{ t }\left( j \right) } }\)

주목할 점은 분자의 조건문은 $j$번째 상태이면서 그 때 관측치$o_t$가 $v_k$일 확률을 의미. $v_k$가 나타나지 않는 $\gamma$는 0으로 무시 함. 즉, 분자부를 계산 시 관측치 시퀀스에서 관측 값이 $v_k$인 group에 대한 sum을 구하면 된다 (코드 링크를 걸어 둠).

Decoding

\[{ v }_{ t }(j)=\max _{ i =1, 2, .., N }{ \left[ { v }_{ t-1 }(i)\times { a }_{ ij }\times { b }_{ j }({ o }_{ t }) \right] }\]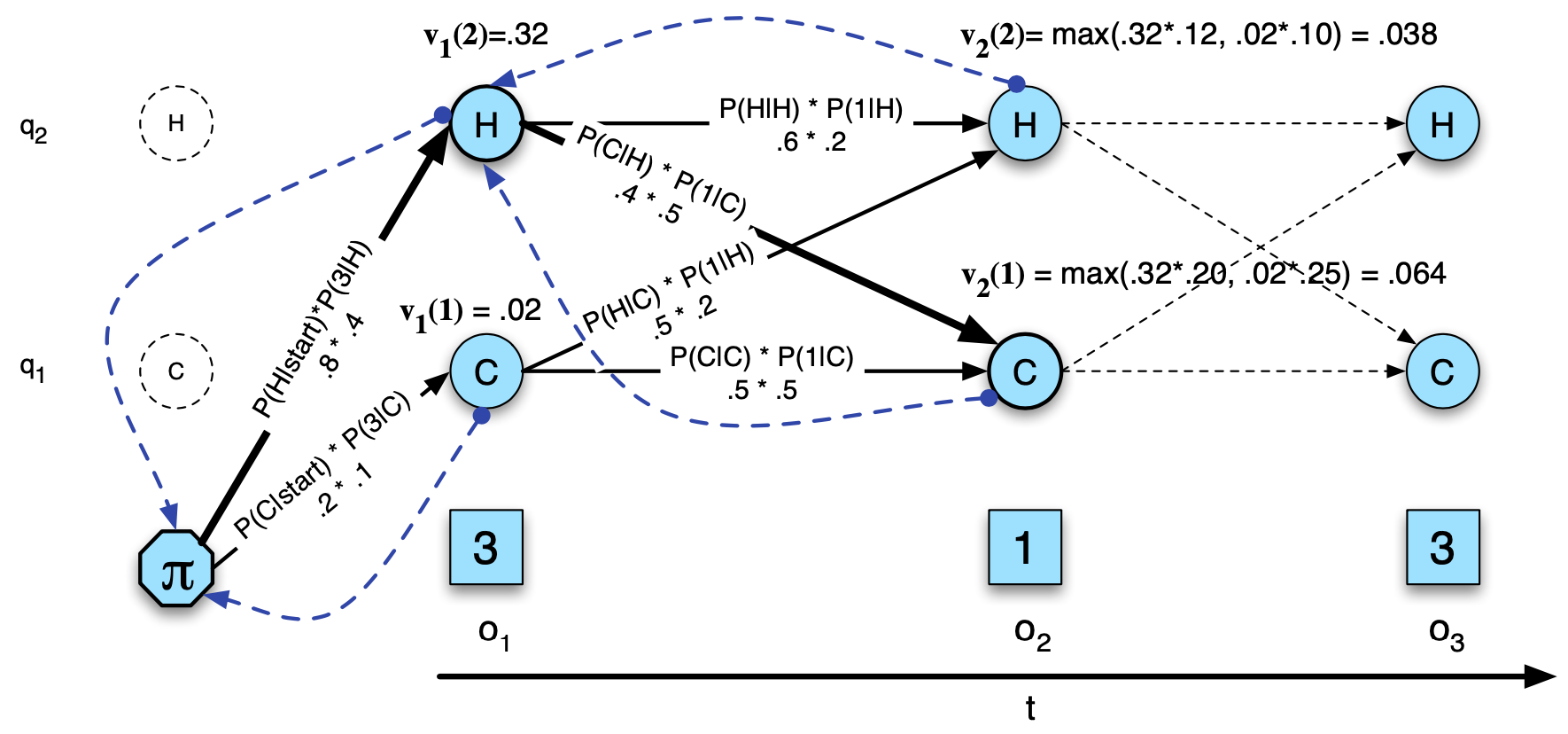

Remark

HMM은 다음과 같이 3가지 문제를 푸는것으로 설명된다.

1. Evaluation problem: dynamic programing 방식을 사용하여 효율적으로 forward 혹은 backword 방식으로 likelihood를 계산한다.
2. Decoding problem: dynamic programming 방식을 사용하여 observation 에 대한 optimal 한 hidden state 를 찾는다.
3. Learning problem: trainsition probability와 emission probability를 학습한다. 특히 observation 시퀀스만 주어지면 EM-algorithm으로 unsupervised 학습을 할수 있다.

Implementation and Unittest

├── hmm.py
├── image
├── README.md
└── toy_hmm.py

Github: PythonHMM 에서 hmm.py 에 구현이 되어있다. 좀더 잘 구현되어있는 Github: hmmlearn 도 있지만 이해하기 더 쉬운 PythonHMM을 분석해보고 unittest 코드도 추가해보았다. evaluation, decode, learning problem에 대해 각각 테스트하게 된다.

python -m unittest toy_hmm.py

Question 1: train할때 unsupervised learning이기 때문에 사실 observation 값들만 필요하고, 각 시점의 state 값들은 필요하지 않은데, 이 구현체의 경우에는 넣도록 되어있다. 실제로 사용하지도 않는다. (hmmlearn 의 경우 hmm.Multinomial.fit을 통해 학습하는데 state 값들은 필요없다.)

내 생각: accuracy 측정을 위해 집어 넣도록 한것일지도 모르겠다.

Question 2: 구현체에서 초기 모델 파라미터 셋팅시 train에 사용할 observation sequence들의 통계정보를 곧바로 적용한다. 이렇게 곧바로 적용해버리면 오버피팅될 경향이 있는것 같은데… 이렇게 구현되어있다.

내 생각: EM 알고리즘은 초기값에 따라 변동이 심하기로 유명하기 때문에 일부러 안정성을 위해 그렇게 한것 같다.

hmmlearn

간단 사용법 정리

hmm = MultinomialHMM(n_components=2, n_iter=0, params='', init_params='')                                                                                                    
hmm.startprob_ = [0.8, 0.2]
hmm.transmat_ = [[0.6, 0.4], [0.5, 0.5]]
hmm.emissionprob_ = [[0.2, 0.4, 0.4], [0.5, 0.4, 0.1]]
# TODO: sampling (model should be pretrained.)
size = 5000
numseq = 500                                                                                                                                                                 print(f"Sampling {size} obervations, split {numseq} sequences with size {size // numseq}.")
X, Z = hmm.sample(size)  # X: observations, Z: hidden states
samples, states  = hmm.sample(10)
lengths = [len(X) // numseq] * numseq

# TODO: Evaluation Problem
toy_ex = [[3], [1], [3]] # n_samples x n_dim
loglikelihood = hmm.score(toy_ex, lengths=[len(toy_ex)])
print(f"loglikelihood({toy_ex})={loglikelihood:.6f}")

# TODO: Decoding Problem
logprob, predstates = hmm.decode(toy_ex, lengths=[len(toy_ex)])
print(f"likelihood: {math.exp(logprob):.6f}, predstates: {convert_states(config, predstates, inverse=True)}")

# TODO: Learn problem
hmm = MultinomialHMM(n_components=2, n_iter=10, tol=1e-4, params='ste', init_params='ste', verbose=True)
hmm.fit(X, lengths)

Reference

[1] https://web.stanford.edu/~jurafsky/slp3/A.pdf

[2] https://ratsgo.github.io/machine%20learning/2017/03/18/HMMs/

[3] https://ratsgo.github.io/speechbook/docs/am/hmm

[4] https://youtu.be/HB9Nb0odPRs

[5] https://github.com/jason2506/PythonHMM/

Furthermore

[1] HMM 기반 한국어 형태소 분석기 Github