MPC
Introduction
MPC는 Model Predictive Control로 프로세스를 간략히 말하면 다음과 같다.
설계된 모델에 따라서 일정 기간동안의 로봇의 다음 상태를 예측한다.
예측된 상태, 제어변수 와 현재의 상태, 제어변수를 가지고
설계된 목적함수와 제약사항에 대한 값을 계산한다.
이후 최적화를 통해서 다음 상태에 대한 제어 sequence를 찾아내는 방법이다.
Design of Cost and Constraints
비용함수는 일반적으로 다음과 같은 3개의 항의 결합으로 구한다.
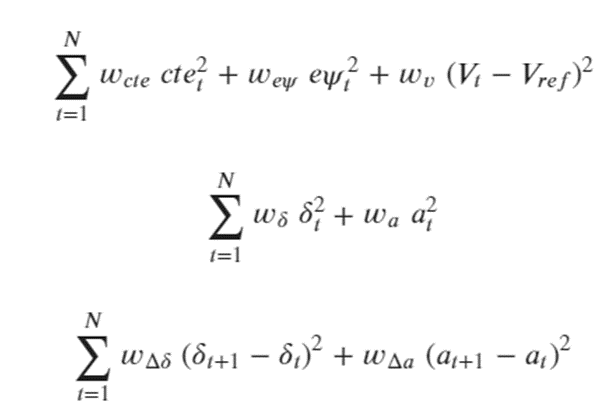
각 항의 의미는 다음과 같다.
• Desired state와 current state간 차이
• Control 변수의 사용
• Control 변수의 변화량
Desired state는 reference trajectory 를 통해서 찾는다.
next state와 next control은 매스텝 optimization을 통해 구한다.
next state는 차량이동체에서 가장 단순히 모델링하면 bicycle model을 주로 사용하고 다음과 같다.
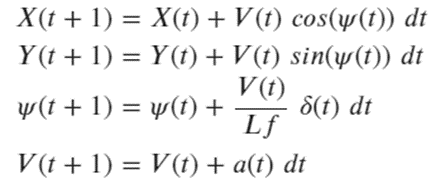
제약사항은 다음과 같은 조건을 주로사용한다.
•Vehicle kinematics 에 근거한 system dynamics 모델 •Control 변수의 혹은 속도의 한계 가동범위
Process
MPC의 전체 process를 요약하면 다음과 같은 과정을 통해서 진행된다.
• Trajectory paths 를 the vehicle-centric reference frame 으로 변환
• Polynomial function 으로 주어진 path를 fitting (QR분해를 이용한 최소제곱법을 통해서)
• cte 와 eψ 를 계산하여 현 스텝에 대한 state error를 구함
• Model variable을 초기화하고 각 변수에 constraint 에 맞는 limit 을 할당
• System 과 physics constraint 를 고려 trajectory cost를 최적화하는 N step의 control 구함
• Optimization 방법 사용하여 control sequence
• Optimize한 첫번째 command를 실행
코드
전처리
1
cx, cy, cyaw, ck = get_switch_back_course(dl)
get_switch_back_course 에서는 주어진 길이 간격으로
따라가야할 경로의 위치, 방향, 그리고 곡률 에 대한 리스트를 반환한다.
이후 참조할 target speed profile을 heuristic 한 rule에 따라서 먼저 계산한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
sp = calc_speed_profile(cx, cy, cyaw, TARGET_SPEED)
def calc_speed_profile(cx, cy, cyaw, target_speed):
speed_profile = [target_speed] * len(cx)
direction = 1.0 # forward
# Set stop point
for i in range(len(cx) - 1):
dx = cx[i + 1] - cx[i]
dy = cy[i + 1] - cy[i]
move_direction = math.atan2(dy, dx)
if dx != 0.0 and dy != 0.0:
dangle = abs(pi_2_pi(move_direction - cyaw[i]))
if dangle >= math.pi / 4.0:
direction = -1.0
else:
direction = 1.0
if direction != 1.0:
speed_profile[i] = - target_speed
else:
speed_profile[i] = target_speed
speed_profile[-1] = 0.0
return speed_profile
따라가야할 path에 대한 displacement vector와 path의 접선의 각도 차를 고려했을 때
$\pi/4$ 보다 크다면 상수의 target speed를 뒤집어서 후진을 하도록 바꾼다.
마지막으로 목적지에 도달한다면 target speed를 0으로 한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
t, x, y, yaw, v, d, a = do_simulation(
cx, cy, cyaw, ck, sp, dl, initial_state)
class State:
"""
vehicle state class
"""
def __init__(self, x=0.0, y=0.0, yaw=0.0, v=0.0):
self.x = x
self.y = y
self.yaw = yaw
self.v = v
self.predelta = None
차량의 상태는 현재 위치, 방향, 그리고 속도의 값을 갖는다.
차량의 상태를 초기화하고 이제 시뮬레이션으로 넘어간다.
시뮬레이션 루프
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
def do_simulation(cx, cy, cyaw, ck, sp, dl, initial_state):
"""
Simulation
cx: course x position list
cy: course y position list
cy: course yaw position list
ck: course curvature list
sp: speed profile
dl: course tick [m]
"""
goal = [cx[-1], cy[-1]]
state = initial_state
# initial yaw compensation
if state.yaw - cyaw[0] >= math.pi:
state.yaw -= math.pi * 2.0
elif state.yaw - cyaw[0] <= -math.pi:
state.yaw += math.pi * 2.0
time = 0.0
x = [state.x]
y = [state.y]
yaw = [state.yaw]
v = [state.v]
t = [0.0]
d = [0.0]
a = [0.0]
target_ind, _ = calc_nearest_index(state, cx, cy, cyaw, 0)
odelta, oa = None, None
cyaw = smooth_yaw(cyaw)
while MAX_TIME >= time:
xref, target_ind, dref = calc_ref_trajectory(
state, cx, cy, cyaw, ck, sp, dl, target_ind)
x0 = [state.x, state.y, state.v, state.yaw] # current state
oa, odelta, ox, oy, oyaw, ov = iterative_linear_mpc_control(
xref, x0, dref, oa, odelta)
if odelta is not None:
di, ai = odelta[0], oa[0]
state = update_state(state, ai, di)
time = time + DT
x.append(state.x)
y.append(state.y)
yaw.append(state.yaw)
v.append(state.v)
t.append(time)
d.append(di)
a.append(ai)
if check_goal(state, goal, target_ind, len(cx)):
print("Goal")
break
스텝별 전처리
각 함수가 어떤 의미를 지니는지 살펴보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def calc_nearest_index(state, cx, cy, cyaw, pind):
dx = [state.x - icx for icx in cx[pind:(pind + N_IND_SEARCH)]]
dy = [state.y - icy for icy in cy[pind:(pind + N_IND_SEARCH)]]
d = [idx ** 2 + idy ** 2 for (idx, idy) in zip(dx, dy)]
mind = min(d)
ind = d.index(mind) + pind
mind = math.sqrt(mind)
dxl = cx[ind] - state.x
dyl = cy[ind] - state.y
angle = pi_2_pi(cyaw[ind] - math.atan2(dyl, dxl))
if angle < 0:
mind *= -1
return ind, mind
calc_nearest_index에서 경로에서 N_IND_SEARCH 만큼의 윈도우 내에서
수직거리가 가장 가까운 index 를 찾아낸다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def smooth_yaw(yaw):
for i in range(len(yaw) - 1):
dyaw = yaw[i + 1] - yaw[i]
while dyaw >= math.pi / 2.0:
yaw[i + 1] -= math.pi * 2.0
dyaw = yaw[i + 1] - yaw[i]
while dyaw <= -math.pi / 2.0:
yaw[i + 1] += math.pi * 2.0
dyaw = yaw[i + 1] - yaw[i]
return yaw
smooth_yaw 에서는 주어진 yaw list에서
접선의 기울기 변화량이 $(-\pi/2, \pi / 2)$ 의 범위를 넘어가지 않도록 각도 표현을 바꾼다.
이후 MAX_TIME 까지 미리 control sequence 를 계산한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
def calc_ref_trajectory(state, cx, cy, cyaw, ck, sp, dl, pind):
xref = np.zeros((NX, T + 1))
dref = np.zeros((1, T + 1))
ncourse = len(cx)
ind, _ = calc_nearest_index(state, cx, cy, cyaw, pind)
if pind >= ind:
ind = pind
xref[0, 0] = cx[ind]
xref[1, 0] = cy[ind]
xref[2, 0] = sp[ind]
xref[3, 0] = cyaw[ind]
dref[0, 0] = 0.0 # steer operational point should be 0
travel = 0.0
for i in range(T + 1):
travel += abs(state.v) * DT
dind = int(round(travel / dl))
if (ind + dind) < ncourse:
xref[0, i] = cx[ind + dind]
xref[1, i] = cy[ind + dind]
xref[2, i] = sp[ind + dind]
xref[3, i] = cyaw[ind + dind]
dref[0, i] = 0.0
else:
xref[0, i] = cx[ncourse - 1]
xref[1, i] = cy[ncourse - 1]
xref[2, i] = sp[ncourse - 1]
xref[3, i] = cyaw[ncourse - 1]
dref[0, i] = 0.0
return xref, ind, dref
calc_ref_trajectory 에서는
현재의 index에서 주어진 horizon만큼 reference 상태, 그리고 steer sequence를 초기화 한다.
위의 과정은 현재의 상태에서 주어진 horizon 만큼 따라가야할 path를 fitting한 것을 의미한다.
여기까지 매스텝 mpc control에 대한 전처리가 끝났고 주요 부분으로 넘어가보자.
Iterative MPC Control
1
oa, odelta, ox, oy, oyaw, ov = iterative_linear_mpc_control(xref, x0, dref, oa, odelta)
initial state (x0), reference trajectory (xref, dref), current control (oa, odelta)가 주어졌을 때
iterative_linear_mpc_control 함수에서는 current control (oa, odelta) 과 state (ox, oy, oyaw, ov)를 반환한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def iterative_linear_mpc_control(xref, x0, dref, oa, od):
"""
MPC contorl with updating operational point iteraitvely
"""
if oa is None or od is None:
oa = [0.0] * T
od = [0.0] * T
for i in range(MAX_ITER):
xbar = predict_motion(x0, oa, od, xref)
poa, pod = oa[:], od[:]
oa, od, ox, oy, oyaw, ov = linear_mpc_control(xref, xbar, x0, dref)
du = sum(abs(oa - poa)) + sum(abs(od - pod)) # calc u change value
if du <= DU_TH:
break
else:
print("Iterative is max iter")
return oa, od, ox, oy, oyaw, ov
처음에는 계획된 control sequence가 없으므로 0으로 초기화한다.
Update State
계산된 control을 환경에 이행하고 얻은 다음 state로 다시 현재의 state를 업데이트한다.
마지막으로 현재의 상태가 목표지점인지를 체크하여 종료시킬지를 판별한다.
계산 한계값으로 매 스텝 MAX_ITER 만큼 지정하고 최적화를 반복하게 된다.
각 iteration 마다 최적화는 다음과 같다.
predict_motion 함수에서는 motion model에 따라서
current control (oa, odelta)을 이행한 뒤의 다음 상태 (xbar) 를 유추한다.
initial state (x0), reference trajectory (xref, dref), predicted next state(xbar) 를 가지고
설계된 목적함수를 최적화하는 상태와 control에 대한 sequence를 찾아낸다.
안전장치를 위해서 만약 최적화된 control 변화가 일정 한계값 DU_TH 를 넘어가면 최적화를 중지시킨다.
predict_motion 함수와 linear_mpc_control 가 어떻게 동작하는지 알아보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def predict_motion(x0, oa, od, xref):
xbar = xref * 0.0
for i, _ in enumerate(x0):
xbar[i, 0] = x0[i]
state = State(x=x0[0], y=x0[1], yaw=x0[3], v=x0[2])
for (ai, di, i) in zip(oa, od, range(1, T + 1)):
state = update_state(state, ai, di)
xbar[0, i] = state.x
xbar[1, i] = state.y
xbar[2, i] = state.v
xbar[3, i] = state.yaw
return xbar
def update_state(state, a, delta):
# input check
if delta >= MAX_STEER:
delta = MAX_STEER
elif delta <= -MAX_STEER:
delta = -MAX_STEER
state.x = state.x + state.v * math.cos(state.yaw) * DT
state.y = state.y + state.v * math.sin(state.yaw) * DT
state.yaw = state.yaw + state.v / WB * math.tan(delta) * DT
state.v = state.v + a * DT
if state.v > MAX_SPEED:
state.v = MAX_SPEED
elif state.v < MIN_SPEED:
state.v = MIN_SPEED
return state
predict_motion 에서는 주어진 horizon동안 설계한 모델에 의해서 상태를 천이하여 다음 상태를 예측한다.
update state는 kinematics를 bicycle model에 의해서 상태가 천이하는 것을 볼 수 있다.
안전성을 위해서 한계 steer 와 한계 속도를 넘어가지 않도록 clipping 하는 것을 볼 수 있다.
이제 linear_mpc_control 함수로가서 최적화를 어떻게 하는지 보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
def linear_mpc_control(xref, xbar, x0, dref):
"""
linear mpc control
xref: reference point
xbar: operational point
x0: initial state
dref: reference steer angle
"""
x = cvxpy.Variable((NX, T + 1))
u = cvxpy.Variable((NU, T))
cost = 0.0
constraints = []
for t in range(T):
cost += cvxpy.quad_form(u[:, t], R)
if t != 0:
cost += cvxpy.quad_form(xref[:, t] - x[:, t], Q)
A, B, C = get_linear_model_matrix(
xbar[2, t], xbar[3, t], dref[0, t])
constraints += [x[:, t + 1] == A @ x[:, t] + B @ u[:, t] + C]
if t < (T - 1):
cost += cvxpy.quad_form(u[:, t + 1] - u[:, t], Rd)
constraints += [cvxpy.abs(u[1, t + 1] - u[1, t]) <=
MAX_DSTEER * DT]
cost += cvxpy.quad_form(xref[:, T] - x[:, T], Qf)
constraints += [x[:, 0] == x0]
constraints += [x[2, :] <= MAX_SPEED]
constraints += [x[2, :] >= MIN_SPEED]
constraints += [cvxpy.abs(u[0, :]) <= MAX_ACCEL]
constraints += [cvxpy.abs(u[1, :]) <= MAX_STEER]
prob = cvxpy.Problem(cvxpy.Minimize(cost), constraints)
prob.solve(solver=cvxpy.ECOS, verbose=False)
if prob.status == cvxpy.OPTIMAL or prob.status == cvxpy.OPTIMAL_INACCURATE:
ox = get_nparray_from_matrix(x.value[0, :])
oy = get_nparray_from_matrix(x.value[1, :])
ov = get_nparray_from_matrix(x.value[2, :])
oyaw = get_nparray_from_matrix(x.value[3, :])
oa = get_nparray_from_matrix(u.value[0, :])
odelta = get_nparray_from_matrix(u.value[1, :])
else:
print("Error: Cannot solve mpc..")
oa, odelta, ox, oy, oyaw, ov = None, None, None, None, None, None
return oa, odelta, ox, oy, oyaw, ov
cvxpy 라이브러리를 사용하여 최적화를 한다.
목적함수, 제약사항에 대한 함수, 변수, 그리고 solver를 지정해주면 최적화된 값을 구해주는 편리한 툴이다.
먼저 최적화시 사용한 변수 (x,u) 를 정의한다.
상태의 경우 현재의 상태 + 미래의 상태가 담겨야하기 때문에 길이가 +1이 된다.
initial state (x0), reference trajectory (xref, dref), predicted next state(xbar),
그리고 최적화시 사용한 변수 (x,u) 를 사용하여 cost 와 constraints를 계산하고
solver를 지정해주면 최적화된 상태와 변수에 대한 sequence가 call by reference에 의해서 계산된다.
마지막으로 자료형을 바꾸어서 반환하면 된다.
만약 최적화된 해를 구하지 못하면 예외처리를 해서 마무리한다.
Cost와 Constraint를 어떻게 계산했는지 살펴보자.
1
2
3
4
5
# mpc parameters
R = np.diag([0.01, 0.01]) # input cost matrix
Rd = np.diag([0.01, 1.0]) # input difference cost matrix
Q = np.diag([1.0, 1.0, 0.5, 0.5]) # state cost matrix
Qf = Q # state final matrix
MPC에 사용되는 파라미터는 다음과 같다.
1
2
3
4
5
6
7
8
9
10
11
cost = 0.0
for t in range(T):
cost += cvxpy.quad_form(u[:, t], R)
if t != 0:
cost += cvxpy.quad_form(xref[:, t] - x[:, t], Q)
if t < (T - 1):
cost += cvxpy.quad_form(u[:, t + 1] - u[:, t], Rd)
cost += cvxpy.quad_form(xref[:, T] - x[:, T], Qf)
cost에 대한 계산은 다음과 같다.
control 변수 (u) 에 대해서 R을 계수로하여 제곱합을 구한다.
reference trajectory 의 상태 (xref) 와 현재의 상태 (x) 대한 차이에 대해서 Q를 계수로하여 제곱합을 구한다.
control 변수의 변화량 (u) 에 대해서 Rd을 계수로하여 제곱합을 구한다.
위 식으로 부터 control 변수가 커지지 않고 변화량도 커지지 않고
reference trajectory를 최대한 가깝게 따라가도록 설계됬다는 것을 알 수 있다.
이어서 constraint가 어떻게 계산되는가 보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
constraints = []
for t in range(T):
A, B, C = get_linear_model_matrix(
xbar[2, t], xbar[3, t], dref[0, t])
constraints += [x[:, t + 1] == A @ x[:, t] + B @ u[:, t] + C]
if t < (T - 1):
constraints += [cvxpy.abs(u[1, t + 1] - u[1, t]) <= MAX_DSTEER * DT]
constraints += [x[:, 0] == x0]
constraints += [x[2, :] <= MAX_SPEED]
constraints += [x[2, :] >= MIN_SPEED]
constraints += [cvxpy.abs(u[0, :]) <= MAX_ACCEL]
constraints += [cvxpy.abs(u[1, :]) <= MAX_STEER]
계획된 변수(x, u)가 설계된 모델을 만족하는 지 여부를 체크한다.
계획된 control의 변화가 특정값보다 작은 지를 체크한다.
상태가 초기조건을 만족하는지
계속된 속도, accel, steer가 한계값 이내인지를 체크한다.
모든 제약사항들은 논리식의 리스트 형태로 담기게 된다.
결과
![]()
고찰
역시 많은 한계가 존쟁한다.
실제로 적용하려면 tunning해야할 파라미터가 상당히 많다.
또한 실제로 적용하려면 단순히 bicycle 모델로는 안될 경우가 많을 것이다.
만약 speed profile이 상수가 아니고 시간에 따라 변하는 continuous한 값이라면
값의 overshooting때문에 시스템이 안정적이지 못할 것이다.
시뮬레이션에서도 curvature가 큰 구간은 오버슈팅이 상당히 있는 것을 볼 수 있다.
위와같은 이유로 고도가 존재하는 환경일 경우 시스템이 상당히 불안정할 것이다.


Leave a comment