LEARNING ROBUST REWARDS WITH ADVERSARIAL INVERSE REINFORCEMENT LEARNING
Abstract
현재 DRL은 reward engineering이 필요하다. IRL 방법으로 reward를 찾으려 했으나 unknown dynamics에서 high dimension 문제에서는 한계가 있었다. 즉 dynamics에 robust한 reward function을 복원할 수 있다는 것을 이 논문을 통해서 보인다. 실험에서는 dynamics가 바뀌는 transfer setting을 하고 제안 모델이 이를 잘 풀 수 있음을 보였다.
1. Introduction
기존 IRL 문제는 ambiguous policy와 ambiguous reward문제가 있었다. 전자는 MaxEnt IRL 을 통해 해결됬지 후자는 아직 어려움이 있다. 저자는 dynamics 변화에서 변하지 않는 reward를 disentangled reward라고 말한다. GAIL은 reward를 복원할 수 없고 GCL은 entire trajectory 수준에서 동작하지 않지만 저자가 제안하는 Adversarial IRL (AIRL) 방법은 dynamics를 모르는 continuous, high dimensional task에서 disentangled reward를 학습할 수 있고 복원가능하다.
2. Related Work
흐름은 IRL -> MMP -> MaxEnt IRL 순으로 발전이 이루어졌고 feature matching을 통한 MLE 문제를 풀어서 reward를 찾고자 했으며 generative modeling을 학습하는 것과 연결된다. 전체 GCL에서 학습는 policy와 reward에 대한 EBM의 odd ratio가 discriminator에 대응된다. GCL에서는 전체 trajectory에 대해서 discriminator의 값을 구했지만, 그것은 high variance 때문에 비효율적이므로 본 논문에서는 single state-action pair에 대한 식으로 바꾸었다. 저자는 그 식을 unrestricted form이라고 언급한다. 그런데 단순히 single state-action pair에 대한 식으로 바꾼 것은 환경변화에 reward가 robust하지 않다고 한다. 이러한 문제를 reward ambiguity problem이라고 하며 저자는 이를 해결하기 위한 방법을 제시한다.
3. Background
IRL의 흐름을 익히고자 MaxEnt IRL이란 무엇이며 왜 reward를 찾는게 MLE를 푸는 것이고 GAN으로 이어졌는 그리고 어떻게 reward를 복원할 수 있는지 알아보자.
Maximum causal entropy IRL framework는 entropy regularized MDP 에서 출발한다.
\[\require{color} \pi^{*} = \arg \max_{\pi}\mathbb{E}_{\tau \sim \pi}\bigg[ \sum^{T}_{t=0}\gamma^{t}\bigg(r(s_t,a_t) + H(\pi(\cdot | s_t))\bigg)\bigg]\]위의 식의 해는 아래와 같으며 $Q^{*}_{soft}$ 를 우리는 soft Q-function이라고 한다.
\[\pi^{*}(a|s) \propto e^{Q^{*}_{soft}} \\ Q^{*}_{soft} = r_{t}(s_t, a_t) + \mathbb{E}_{s_{t+1},... \sim \pi}\bigg[ \sum^{T}_{t=t'}\gamma^{t'}\bigg(r(s_{t'},a_{t'}) + H(\pi(\cdot | s_{t'}))\bigg)\bigg]\]IRL에서 우리는 demonstration $\mathcal{D} = {\tau_1, …, \tau_N}$ 으로부터 reward $r(s,a)$ 를 찾기를 원한다. 그래서 Demonstration의 분포를 dynamics가 변하지 않고 deterministic하다는 가정하에 운전자의 의도인 reward 를 파라미터화하여 Energy function으로 사용하여 EBM 에 의거하여 $p_{\theta}$ 를 아래와 같이 두고 MLE 문제를 풀어서 reward를 찾고자 했다. MaxEnt IRL
\[\begin{split} p_{\theta} &\propto p(s_0) \overset{T}{\underset{t=0}{\Pi}} p(s_{t+1}|s_t, a_t) e^{\gamma^{t} r_{\theta }(s_t,a_t)} \\ &\propto e^{ \overset{T}{\underset{t=0}{\sum}} \gamma^{t} r_{\theta }(s_t,a_t)} \\ \max_{\theta} & \mathbb{E}_{\tau \sim D}[\log p_{\theta}(\tau)] \end{split}\]위의 MLE식은 Generator $\pi(\tau)$ 와 이를 평가하는 Discriminator $e^{f_{\theta}(\tau)}$ 를 설정하여 GAN의 optimization식으로 바꿀 수 있다.
\[D_{\theta}(\tau) = \frac{e^{f_{\theta}(\tau)}}{e^{f_{\theta}(\tau)} + \pi(\tau)}\]학습이 완료되면 optimal discriminator로부터 optimal reward function $f^{*}(\tau) = R^{*}(\tau) + const$ 를 복원 할 수 있다. 여기서 상수는 optimal policy를 바꾸지 않으므로 더해줘도 괜찮다.
4. ADVERSARIAL INVERSE REINFORCEMENT LEARNING (AIRL)
full trajectroy를 사용하면 high variance 문제가 있다. 그래서 저자는 아래와 같은 Appendix A를 통해서 single state-action에 대한 식으로 바꾸었다.
\[D_{\theta}(s,a) = \frac{e^{f_{\theta}(s,a)}}{e^{f_{\theta}(s,a)} + \pi(a|s)}\]학습이 완료되면 trajectory-centric case 처럼 optimal reward function $f^{*}(s,a) = \log \pi^{*}(a|s) = A^{*}(s,a)$ 는 optimal policy에 대한 advantage function으로 구해진다. 하지만 위와 같이 바꾸면 imitation 학습측면에서 효과적으로 optimal reward를 찾을 수 있지만 environment dynamics 에 따라 변하는 entangled reward 를 학습하게 되는 문제에 직면한다. 즉, 학습된 reward function은 환경의 변화에 robust하지 않는다. 다음 section에서는 이 문제를 어떻게 해결할 수 있는지 제시한다.
5. THE REWARD AMBIGUITY PROBLEM
이번 section에서는 왜 IRL이 environment 변화에 robust 한 reward를 학습하는데 실패했으며 어떻게 이를 해결할 수 있는지를 제시한다.
왜 dynamics가 바뀌면 같은 reward함수가 다른 optimal policy를 만드는 것일지 생각해보자. 두개의 MDP $M, M’$가 같은 reward를 공유하며 서로 다른 dynamics $T, T’$ 을 갖는다고 하자. 아래와 같은 state-action reward에 대해서 $T(s,a) \rightarrow s’$ 이라고 할 때,
\[\begin{split} \hat{r}(s,a) &= r(s,a) + \gamma \Phi (T(s,a)) - \Phi(s) \\ &\neq r(s,a) + \gamma \Phi (T'(s,a)) - \Phi(s) \end{split}\]이므로 target policy가 서로 달라지게 되는 문제가 발생한다.
Ng et al. (1999) 에서 임의의 함수 $\Phi(s) : \mathcal{S} \rightarrow \mathbb{R}$ 에 대해서 dynamics를 알지 못할 때, optimal policy를 보전할 수 있는 일반화된 아래와 같은 reward의 형태를 제시했다.
\[\hat{r}(s,a,s') = r(s,a,s') + \gamma\Phi(s') - \Phi(s)\]5.1 DISENTANGLING REWARDS FROM DYNAMICS
disentangled reward란 모든 dynamics에 대해서 optimal policy가 invarient 한 reward function을 말하며 이를 어떻게 정의하고 표현할 수 있는지 왜 그 표현이 환경에 robust한지를 Appendix B를 통해서 증명한다.
우선 고정된 reward $r$ 과 dynamics $T$ 에 대한 optimal Q-function과 policy 를 $ Q^{*}_{r,T}(s,a) $ 와 $\pi^{*}_{r,T}(a|s)$ 라고 하자. 이때 우리는 disentangled reward를 Definition 5.1로 다음과 같이 정의 한다.
그리고 dynamics 는 state에 대한 함수 $f(s)$ 와 next state에 대한 함수 $g(s’)$ 에 대해서 두 함수의 합 $f(s) + g(s’)$ 으로부터 isolate가 가능하다는 decomposability condition을 만족한다고 가정한다.
첫번째 Theorem은 ground truth reward $r(s)$ 와 decomposability condition을 만족하는 dynamics $T$ 에 대해서 IRL 알고리즘을 통해서 아래의 식을 만족하는 오직 현재 state 만 dependent한 reward를 복원한다면 그 복원된 reward $r’(s)$ 는 disentangled reward이다.
두번째 Theorem은 복원된 reward $r’(s,a,s’)$ 이 disentangled reward 라면 오직 현재 state에만 dependent하다는 것이다.
다시말해 dynamics가 decomposability condition을 만족한다는 가정하에서 MaxEnt IRL 알고리즘을 통해서 아래의 조건을 만족하는 state 에만 종속적인 임의의 함수 $f(s)$ 중 최적값을 찾게 되면 그것이 disentangled reward임을 의미한다.
6. LEARNING DISENTANGLED REWARDS WITH AIRL
저자는 section 4의 discrimator를 다음과 같이 수정했다.
\[\require{color} D_{\theta, \textcolor{red}{\phi}}(s,a,\textcolor{red}{s'}) = \frac{e^{f_{\theta,\textcolor{red}{\phi}}(s,a, \textcolor{red}{s'})}}{e^{f_{\theta, \textcolor{red}{\phi}}(s,a, \textcolor{red}{s'})} + \pi(a|s)} \\ ,where \; f_{\theta, \phi} (s,a,s') = \underbrace{g_{\theta}(s,a)}_{reward \; approximator} + \underbrace{\gamma h_{\phi}(s') - h_{\phi}(s)}_{shaping \; term}\]위의식에서 shaping term을 더함으로써 환경 변화에 의해서 원하지 않는 reward의 변화를 완화해주는 역할을 하게 된다. 알고리즘은 아래와 같다.
GAIL과 discriminator의 formulation만 약간 다를 뿐 절차는 동일하다.
그런데 reward가 오직 state만 dependent할 때 disentangled reward라고 했으므로 다음과 같이 restricted reward approximator를 설정한다.
\[f_{\theta, \phi} (s,a,s') = \underbrace{g_{\theta}(\textcolor{red}{s})}_{reward \; approximator} + \underbrace{\gamma h_{\phi}(s') - h_{\phi}(s)}_{shaping \; term}\]IRL알고리즘을 통한 최적값은 다음과 같은 관계가 성립한다는 것을 Appendix C에서 보였다.
\[\require{cancel} \begin{split} f^{*}(s,a,s') &= \underbrace{g^{*}(s)}_{r^{*}(s) + \cancel{const}} +\underbrace{\gamma h^{*}(s') - h^{*}(s)}_{\gamma V^{*}(s') + \gamma \cancel{const} - V^{*}(s) - \cancel{const}} \\ &= \underbrace{r^{*}(s) + \gamma V^{*}(s')}_{Q^{*}(s,a)} - V^{*}(s) = A*(s,a) \end{split}\]따라서 우리는 $f_{\theta, \phi}(s,a,s’)$ 를 deterministic dynamics하에서 구한 optimal advantage $A^{*}(s,a)$의 single sample estimator라고 볼 수 있다.
Appendix A. JUSTIFICATION OF AIRL
이번절에서는 AIRL 이 MaxEnt IRL 문제에 대한 trajectory-centric formulation인 GAN-GCL방법과 유사함을 보인다. 수식의 간단함을 위해서 undiscounted case로 가정한다.
A.1 SETUP
section 3. 에서 IRL의 목표는 데이타 분포를 파라미터화하여 근사하고 그 근사 분포의 log likelihood를 최대화하는 것이라고 했다. AIRL 방법은 $p_{\theta}(\tau) = \frac{e^{ \overset{T}{\underset{t=0}{\sum}} r_{\theta }(s_t,a_t)}}{Z_{\theta}}, where \; z_{\theta} = \frac{e^{ \overset{T}{\underset{t=0}{\sum}} r_{\theta }(s_t,a_t)}}{p_{\theta}(\tau)}$ 으로 근사하고 위의 문제를 푼다. 대입하여 미분하면 아래와 같다.
\[\begin{split} \max_{\theta} \mathcal{J}(\theta) =& \max_{\theta} \mathbb{E}_{\tau \sim D}[\log p_{\theta}(\tau)] \\ \frac{\partial}{\partial \theta}\mathcal{J}(\theta) &= \mathbb{E}_{D}[\frac{\partial}{\partial \theta}\log p_{\theta}(\tau)] \\ &= \mathbb{E}_{D}[\overset{T}{\underset{t=0}{\sum}} \frac{\partial}{\partial \theta} r_{\theta }(s_t,a_t)] - \frac{\partial}{\partial \theta} \log Z_{\theta} \\ &= \mathbb{E}_{D}[\overset{T}{\underset{t=0}{\sum}} \frac{\partial}{\partial \theta} r_{\theta }(s_t,a_t)] - \mathbb{E}_{p_{\theta}}[\overset{T}{\underset{t=0}{\sum}}\frac{\partial}{\partial \theta} r_{\theta }(s_t,a_t)] \end{split}\]여기서 두번째 항은 아래와 같이 표현가능하다.
\[\mathbb{E}_{p_{\theta}}[\overset{T}{\underset{t=0}{\sum}}\frac{\partial}{\partial \theta} r_{\theta }(s_t,a_t)] = \int p_{\theta}\overset{T}{\underset{t=0}{\sum}}\frac{\partial}{\partial \theta} r_{\theta }(s_t,a_t) = \int \overset{T}{\underset{t=0}{\sum}}p_{\theta} \frac{\partial}{\partial \theta} r_{\theta }(s_t,a_t)\]이때, 아래와 같이 현재의 state-action에 대한 marginal 분포로 표현하여 다시쓰면 아래와 같다.
\[p_{\theta, t}(s_t, a_t) = \int_{s_{t'=t},a_{t'=t}} p_{\theta}(\tau) \\ \frac{\partial}{\partial \theta}\mathcal{J}(\theta) = \mathbb{E}_{D}[\overset{T}{\underset{t=0}{\sum}} \frac{\partial}{\partial \theta} r_{\theta }(s_t,a_t)] - \mathbb{E}_{p_{\theta, t}}[ \frac{\partial}{\partial \theta} r_{\theta }(s_t,a_t)]\]위의식에서 $p_{\theta,t}$는 rough한 분포 추정이므로 mixture policy $\mu(a|s) = \frac{1}{2}\pi(a|s) + \frac{1}{2} \hat{p}(a|s)$ 를 사용하여 importance sampling을 하면 variance를 줄일 수 있다고 한다. 식은 아래와 같다.
\[\frac{\partial}{\partial \theta}\mathcal{J}(\theta) = \mathbb{E}_{D}[\overset{T}{\underset{t=0}{\sum}} \frac{\partial}{\partial \theta} r_{\theta }(s_t,a_t)] - \mathbb{E}_{\mu_t}[ \frac{p_{\theta, t}(s_t,a_t)}{\mu_{t}(s_t,a_t)}\frac{\partial}{\partial \theta} r_{\theta }(s_t,a_t)]\]위의 결과는 AIRL 방법이 MaxEnt IRL의 cost objective와 동일하는 것을 의미한다.
그리고 policy = generator = sampler $\pi (\tau)$ 의 목적은 우리가 근사한 데이터 분포 $p_{\theta}(\tau)$ 와 같도록 하는 것이다. 따라서 objective는 아래와 같다.
\[\underset{\pi}{min}D_{KL}(\pi (\tau) || p_{\theta}(\tau))\]AIRL에서는 policy trajectory distribution을 다음과 같이 factorize한다.
\[\pi (\tau) = p(s_0) \overset{T-1}{\underset{t=0}{\Pi}} p(s_{t+1}|s_t, a_t) \pi(a_t|s_t) \\ p_{\theta} (\tau) = p(s_0) \overset{T-1}{\underset{t=0}{\Pi}} p(s_{t+1}|s_t, a_t)\frac{e^{r_{\theta }(s_t,a_t)}}{Z_{\theta}}\]그리고 다시 objective에 대입하면 아래와 같이 정리되고 Z는 $\pi$에 무관하므로 최적화 식에서 무시될 수 있다.
\[\require{cancel} \begin{split} - D_{KL}(\pi (\tau) || p_{\theta}(\tau)) &= \mathbb{E}_{\pi}[\log\frac{p_{\theta}(\tau)}{\pi (\tau)}] \\ &= \mathbb{E}_{\pi}[\log \frac{\frac{1}{Z_{\theta}} \cancel{p_(s_0)} \underset{t}{\Pi} \cancel{p(s_{t+1}|s_t, a_t)} e^{r(s_t,a_t)}} { \cancel{p_(s_0)} \underset{t}{\Pi} \cancel{p(s_{t+1}|s_t, a_t)} \pi(a_t| s_t)}] \\ &= \mathbb{E}_{\pi}[(\sum_{t} r(s_t, a_t) - \log \pi(a_t |s_t)) - \log Z] \\ \underset{\pi}{min} - D_{KL}(\pi (\tau) || p_{\theta}(\tau)) &= \underset{\pi}{min} \mathbb{E}_{\pi}[(\sum_{t} r(s_t, a_t) - \log \pi(a_t |s_t)) - \cancel{\log Z}] \\ &= \underset{\pi}{min} \mathbb{E}_{\pi}[\sum_{t} r(s_t, a_t) - \log \pi(a_t |s_t)] \end{split}\]마찬가지로 위의 결과는 AIRL 방법이 MaxEnt IRL의 sampler objective와 동일하는 것을 의미한다.
\[D_{\theta}(s,a) = \frac{e^{f_{\theta}(s,a)}}{e^{f_{\theta}(s,a)} + \pi(a|s)}\]AIRL에서는 GAN구조이기 때문에 위의 식과 같이 바꾼 discriminator를 사용하여 MaxEnt IRL의 cost objective를 discriminator의 objective로 대체하고 MaxEnt IRL의 policy의 objective를 generator의 objective로 대체한다. object식은 아래와 같다.
\[\mathcal{L}_{\theta} (s,a) = - \overset{T}{\underset{t=0}{\sum}}\mathbb{E}_{D}[\log \underbrace{D_{\theta,\phi}(s_t,a_t)}_{\rightarrow 1}] - \mathbb{E}_{\pi_t} [\log (1 - \underbrace{D_{\theta,\phi}(s_t,a_t)}_{\rightarrow 0})] \\ \hat{r}(s,a) = \log(\underbrace{D_{\theta}(s,a)}_{\rightarrow 1}) - \log(1- \underbrace{D_{\theta}(s,a)}_{\rightarrow 1})\\\]A.2 DISCRIMINATOR OBJECTIVE
이어서 이번절에서는 AIRL의 discriminator objective가 MaxEnt cost objective랑 같음을 보인다. 저자가 제시한 discriminator는 아래와 같다.
\[D_{\theta}(s_t,a_t) = \frac{e^{f_{\theta}(s_t,a_t)}}{e^{f_{\theta}(s_t,a_t)} + \pi(a_t |s_t)}\]Discriminator의 objective에서 min 문제를 -max문제로 바꾸고 미분한 것이MaxEnt IRL의 식과 동일함을 보였다. 과정은 아래와 같다.
\[\begin{split} -\mathcal{L}_{\theta} (s,a) &= \overset{T}{\underset{t=0}{\sum}}\mathbb{E}_{D}[ \log D_{\theta,\phi}(s_t,a_t) ] + \mathbb{E}_{\pi_t} [\log (1 - D_{\theta,\phi}(s_t,a_t))] \\ &= \overset{T}{\underset{t=0}{\sum}}\mathbb{E}_{D}[ \log \frac{e^{f_{\theta}(s_t,a_t)}}{e^{f_{\theta}(s_t,a_t)} + \pi(a_t|s_t)} ] + \mathbb{E}_{\pi_t} [\log \frac{\pi(a_t|s_t)}{e^{f_{\theta}(s_t,a_t)} + \pi(a_t|s_t)}] \\ &= \overset{T}{\underset{t=0}{\sum}}\mathbb{E}_{D}[f_{\theta}(s_t,a_t)] + \mathbb{E}_{\pi_t}[\log \pi(a_t|s_t)] -\mathbb{E}_{D}[ e^{f_{\theta}(s_t,a_t)} + \pi(a_t|s_t)] - \mathbb{E}_{\pi_t} [e^{f_{\theta}(s_t,a_t)} + \pi(a_t|s_t)] \\ &= \overset{T}{\underset{t=0}{\sum}}\mathbb{E}_{D}[f_{\theta}(s_t,a_t)] + \mathbb{E}_{\pi_t}[\log \pi(a_t|s_t)] -2\mathbb{E}_{\bar{\mu_t}} [ e^{f_{\theta}(s_t,a_t)} + \pi(a_t|s_t)] \end{split}\]$\theta$ 에 대해서 미분하면 아래와 같다.
\[-\frac{\partial}{\partial \theta} \mathcal{L}_{\theta} (s,a) = \overset{T}{\underset{t=0}{\sum}} \mathbb{E}_{D}[\frac{\partial}{\partial \theta}f_{\theta}(s_t,a_t)] - \mathbb{E}_{\bar{\mu_t}}[ \frac{e^{f_{\theta}(s_t,a_t)} }{\frac{1}{2}e^{f_{\theta}(s_t,a_t)} + \frac{1}{2}\pi(a_t|s_t) } \frac{\partial}{\partial \theta} f_{\theta}(s_t,a_t)]\]이후 두번째 항에서 state margin $\pi(s_t) = \int_a \pi(s_t,a_t)$ 을 분모분자에 곱하면 분모 분자는 아래와 같이 정리된다.
\[(\frac{1}{2}e^{f_{\theta}(s_t,a_t)} + \frac{1}{2}\pi(a_t|s_t))\pi(s_t) = \hat{\mu}(a_t|s_t) \pi(s_t) = \hat{\mu}(s_t,a_t) \\ e^{f_{\theta}(s_t,a_t)} \pi(s_t) = \hat{p}_{\theta,t}(a_t|s_t)\pi(s_t) = \hat{p}_{\theta, t}(s_t,a_t)\]따라서 아래와 같이 정리 된다. 이 식은 MaxEnt IRL의 cost식과 동일하다.
\[-\frac{\partial}{\partial \theta} \mathcal{L}_{\theta} (s,a) = \overset{T}{\underset{t=0}{\sum}} \mathbb{E}_{D}[\frac{\partial}{\partial \theta}f_{\theta}(s_t,a_t)] - \mathbb{E}_{\bar{\mu_t}}[ \frac{\hat{p}_{\theta, t}(s_t,a_t) }{\hat{\mu}(s_t,a_t) } \frac{\partial}{\partial \theta} f_{\theta}(s_t,a_t)]\]A.3 POLICY OBJECTIVE
이번 절에서는 AIRL의 policy objective가 MaxEnt IRL의 policy objective와 같음을 보인다. Generator의 objective에 AIRL의 discriminator의 식을 넣으면 기존의 식과 동일하다는 것을 보였다. 과정은 아래와 같다.
\[\begin{split} \hat{r}(s,a) &= \log(D_{\theta}(s,a)) - \log(1- D_{\theta}(s,a)) \\ &= \log\frac{e^{f_{\theta}(s,a)}}{ \cancel{e^{f_{\theta}(s,a)} + \pi(a|s)}} - \log \frac{ \pi(a|s)}{\cancel{e^{f_{\theta}(s,a)} + \pi(a|s)}} \\ &= f_{\theta}(s,a) - \log \pi(a|s) \\ \mathbb{E}_{\pi}\bigg[\overset{T}{\underset{t=0}{\sum}} \hat{r}(s_t,a_t) \bigg] &= \mathbb{E}_{\pi}\bigg[ \overset{T}{\underset{t=0}{\sum}} f_{\theta}(s_t,a_t) - \log \pi(a_t|s_t)\bigg] \end{split}\]A.4 $f_{\theta}(s, a)$ RECOVERS THE ADVANTAGE
dicriminator는 최종적으로 $\pi \rightarrow \pi_E $ 가 되도록 만든다. 최적해는 아래와 같이 정리 될 수 있다.
\[\pi^{*}(a|s) = e^{f^{*}(s,a)} = \pi_E = e^{A^{*}} \\ f^{*}(s,a) = \log \pi_E = A^{*}\]따라서 $f_{\theta}$ 는 advantage의 estimator가 된다.
Appendix B. STATE-ONLY INVERSE REINFORCEMENT LEARNING
이번절에서는 Decomposability Condition 이 무엇인지 정의하고 Theorems 5.1 and 5.2 을 증명한다.
Definition B.1 (Decomposability Condition)
내용은 아래와 같이 MDP의 모든 state가 linked 되어있을 때 Transition distribution T은 decomposability condition을 만족한다고 한다.
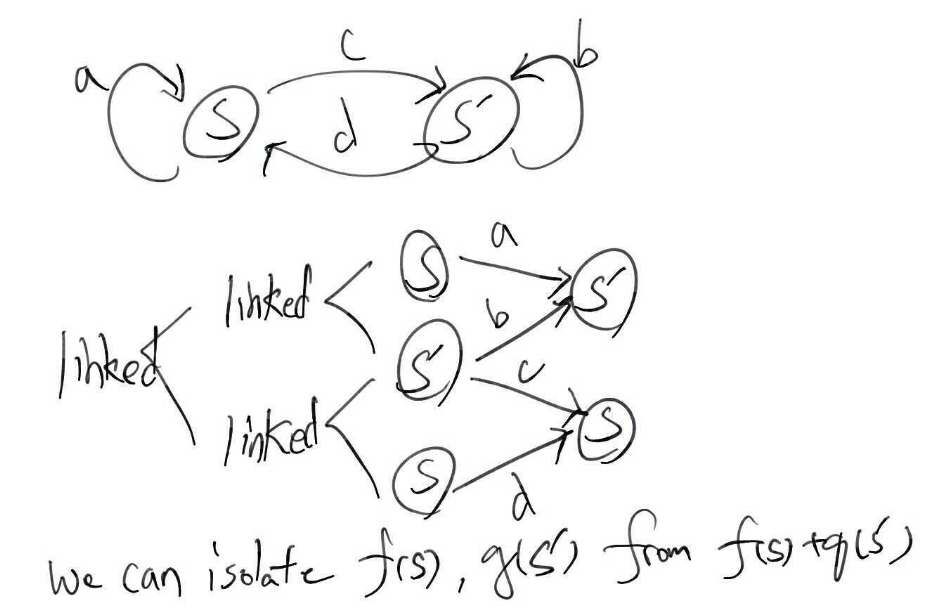
Lemma B.1
Lemma B.1의 내용은 위와같은 decomposability condition을 만족하는 MDP의 dynamics에서 isolation을 통해서 상수값의 bias만 갖고 reward 함수를 복원할 수 있음을 보인다. 이 말은 dynamics변화에도 상수값의 bias만 갖는 true reward를 복원할 수있으면 dynamics변화에 invariant optimal policy를 구할 수 있음을 암시한다. 증명과정은 다음과 같다.
\[a(s) + b(s') = c(s) + d(s') \\ a(s) - c(s) = d(s') - b(s') = const \\ \therefore a(s) = c(s) + const \\ \therefore b(s') = d(s') + const\]위의 MDP flow chart에서 맨 오른쪽 s와 s’의 reward를 isolate하면 decomposability condition에 의해서 아래와 같은 수식을 만족하고 이를 이항정리하고 상수값을 설정하면 증명이 완료된다.
Theorem 5.1
이어서 우리는 ground truth reward가 state에만 의존하며 MDP의 dynamics가 decomposability condition을 만족한다고 가정했을 때 아래의 식에 의해서 reward를 복원하면 disentagled reward임 을 보인다.
\(Q^{*}_{r', T}(s,a) = Q^{*}_{r,T}(s,a) - f(s)\) 증명과정은 이와같이 우리가 학습하는 reward $r’(s) = r(s) + \phi(s)$ 에 오직 state에만 dependent한 임의의 함수가 더해진다고 놓고 위의 식을 IRL로 풀면 과연 state dependent한 임의의 함수가 상수가 되는지 $\phi(s) = const$ 보이면 된다.
\[\begin{split} Let \; r'(s) &= r(s) + \phi(s) \\ Q^{*}_r (s,a) &= r(s) + \gamma \mathbb{E}_{s'} [\underset{a'}{softmax}Q^{*}_{r}(s',a')] \\ Q^{*}_r (s,a) \textcolor{red}{- f(s)} &= r(s)\textcolor{red}{-f(s)} + \gamma \mathbb{E}_{s'} [\underset{a'}{softmax}Q^{*}_{r}(s',a')] \\ Q^{*}_r (s,a) - f(s) &= r(s) \textcolor{red}{+\gamma\mathbb{E}_{s'}[f(s')]} -f(s) + \textcolor{red}{\gamma \mathbb{E}_{s'}} [\underset{a'}{softmax}Q^{*}_{r}(s',a') \textcolor{red}{-f(s')}] \\ Q^{*}_{r'} (s,a) &= r(s) +\gamma\mathbb{E}_{s'}[f(s')] -f(s) + \gamma \mathbb{E}_{s'} [\underset{a'}{softmax}Q^{*}_{r'}(s',a')] \\ Q^{*}_{r'} (s,a) &= r'(s) + \gamma \mathbb{E}_{s'} [\underset{a'}{softmax}Q^{*}_{r'}(s',a')] \\ &,where \;\;r'(s) = r(s) +\gamma\mathbb{E}_{s'}[f(s')] -f(s)= r(s) + \phi(s) \end{split}\]위의 결론에서 decomposability condition하에서 $\phi(s) = \gamma\mathbb{E}_{s’}[f(s’)] -f(s) = const$ 가 되므로 $f(s)=const$ 임을 의미한다.
Theorem 5.2
이번 절에서는 theorem 5.1에서 state only dependent ground truth로 가정하는 것의 타당함을 증명한다. 아래 공식에 의해 disentangled reward를 복원하면 오직 state 에만 의존하며 disentangled reward임을 보인다. 증명방식은 귀류법을 통해 증명한다. 복원된 state가 state 만 의존하는 것이 아닐 때 disentangle reward가 아님을 보이면 된다. 다시말해 r’(s,a,s’) 로 두고 구하면 optimal policy가 바뀌는 것을 보이면 된다.
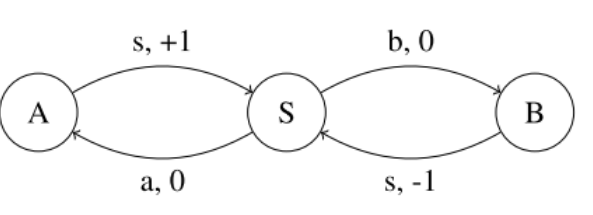
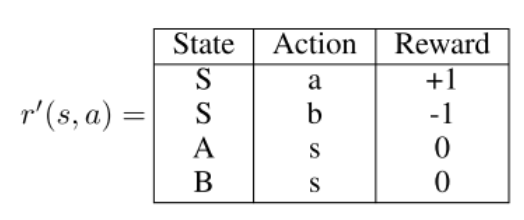
위의 상황에서 state와 action에 dependent한 reward를 복원하게 되면 아래와 같을 수 있다. 이때 s 상태에서 optimal action는 a가 된다.
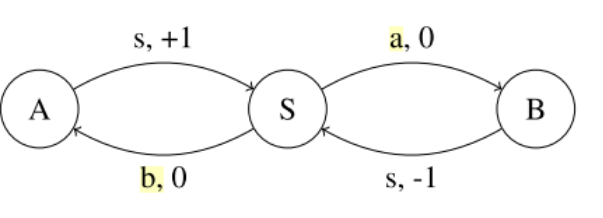
그런데 transition이 아래와 같이 바뀌었다면 state S에서의 action a와 b에 해당되는 reward가 바뀔 것이고 이때의 optimal한 action는 b가 된다.
optimal policy가 변했기 때문에 위에서 구한 reward는 disentangled reward가 아니다. reward가 오직 state에 만 dependent 하다면 shaping potential 은 $\phi(S)=0, \phi(A)=1, \phi(B)=-1$ 로 구해질 것이고 transition이 바뀌더라도 optimal한 policy를 바꾸지 않게 된다.
Appendix C. AIRL RECOVERS REWARDS UP TO CONSTANTS
이번절에서는 AIRL 알고리즘이 ground truth reward를 오직 state-dependent하게 두었을 때 상수 bias를 갖고 복원할 수 있음을 보인다.
Theorem C.1
decomposability condition을 만족하고 deterministic dynamics 하에서 $f(s,a,s’) = g_{\theta}(s) - \gamma h_{\phi} - h_{\phi} $ 로 두고 AIRL로 optimal f를 복원하면 optimal reward 와 optimal value function을 복원할 수 있음을 보인다.
\[\begin{split} f^{*}(s,a,s') &= A^{*}(s,a) & \mbox{,from Appendix A.4} \\ &= Q^{*}(s,a) - V^{*}(s) = r(s) + \gamma V^{*}(s') - V^{*}(s) \\ &= g^{*} + \gamma h^{*}(s') - h^{*}(s) \\ &= \underbrace{r(s) - V^{*}(s)}_{a(s)} + \underbrace{\gamma V^{*}(s')}_{b(s')} & \mbox{,from Lemma B.1} \\ &= \underbrace{g^{*}(s) - h^{*}(s)}_{c(s) = a(s)+ const} + \underbrace{\gamma h^{*}(s')}_{d(s') = b(s')+ const} \end{split}\]AIRL 코드 분석
train_gym.py
- argument 불러오기
- 랜덤씨드 설정
- output directory 설정
- environment 생성
- observation 값 normalization
- action space type에 따라서 policy 모델 instance 생성
- optimizer 생성
- optimizer의 wieght decay 여부 결정
- PPO algorithm의 경우
- ppo기반 agent 생성
- GAIL algorithm의 경우
- 데모 데이타 불러오기
- GAIL기반 Discriminator 생성
- GAIL기반 agent 생성
- AIRL algorithm의 경우
- 데모 데이타 불러오기
- AIRL 기반 Discriminator 생성
- AIRL 기반 agent 생성
- load 사용여부에 따라 agent load
- demo 가 True일 경우
- test를 위한 환경 생성
- test결과 출력 및 저장
- demo 가 False일 경우
- learning rate linear 하게 0으로 감소시키는 hook함수 생성
- clipping parameter를 linear하게 0 으로 감소시키는 hook 함수 생성
- agent training 과 evaluation번갈아하기
- 결과 저장
discriminator.py
Discriminator class
- init
- reward, value network생성
- reward, value network의 optimizer생성 및 초기화
- train
- 입력: expert state, expert next_state, expert_action_prob, fake_states, fake_next_states, fake_action_probs, gamma
- logit 구하는 함수 정의
-
\[\begin{split} D_{\theta, \textcolor{red}{\phi}}(s,a,\textcolor{red}{s'}) &= \frac{e^{f_{\theta,\textcolor{red}{\phi}}(s,a, \textcolor{red}{s'})}}{e^{f_{\theta, \textcolor{red}{\phi}}(s,a, \textcolor{red}{s'})} + \pi(a|s)} \\ &= \frac{1}{1+e^{-(f_{\theta, \phi} (s,a,s') - \log \pi(a|s))}}\\ ,where \;\; &f_{\theta, \phi} (s,a,s') - \log \pi(a|s) \\ &= \underbrace{g_{\theta}(\textcolor{red}{s})}_{reward \; approximator} + \underbrace{\gamma h_{\phi}(s') - h_{\phi}(s)}_{shaping \; term} - \log \pi(a|s) \end{split}\]
-
- discriminator의 loss 구하기
-
\[\mathcal{L}_{\theta} (s,a,s') = - \mathbb{E}_{D} [\log D_{\theta,\phi}(s,a,s')] - \mathbb{E}_{\pi} [\log (1 - D_{\theta,\phi}(s,a,s'))]\]
- 첫번째 항은 sigmoid 출력이 1 두번째 항은 sigmoid 출력이 0 이 나오도록
-
loss 입장에서는 최소화해야되니 -logit을 입력으로 넣어 0을 출력하도록 함
-
log(sigmoid(logits))를 softplus(logits)로 구하면 범위가 [-inf,0] 에서 [0, inf]로 바꾸어 0이 나오는 것을 목표로 하면 학습 안정에 도움이 됨.
-
-
- auto gradient 계산
- optimizer update (learning rate, cliping rate)
airl.py
AIRL agent
- ppo 상속
- init
- discriminator instance를 매서드 변수로
- demonstration loader 불러오기
- discriminator loss, reward 저장 container 선언
- update
- rollout dataloader 불러오기
- observation 의 normalize 여부 결정
- rollout dataloader 로부터 batch단위로 s,a,s’ 불러오기
- demo dataloader로부터 batch단위로 expert s,a,s’ 불러오기
- policy model로부터 s,a pair를 사용하여 action_log_probs 구하기
- policy model로부터 expert s,a pair를 사용하여 demo_action_log_probs 구하기
- discriminator loss구하기
- Update both the policy and the value function with rollout data
-
update_if_dataset_is_ready
-
state only reward를discriminator의 reward를 사용해서 memory에서 reward를 update
\[\hat{r}(s) = g_{\theta}(s)\]
-
-
get_probs
- policy model을 사용하여 state action을 입력받아 log probability를 계산
-
get_statistics
- 평균 discriminator loss, reward, 분산값을 반환

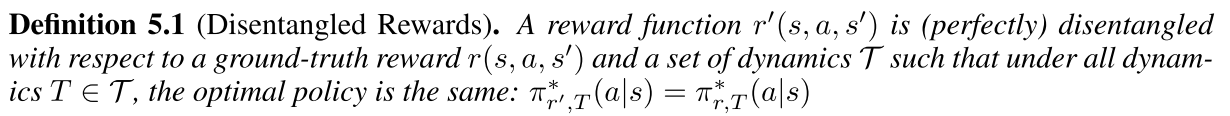



Leave a comment