sw Yoo

sw Yoo

No sweat, no sweet

Global 좌표와 Local좌표의 변환방법을 알아보자

In [1]: 
1
2
3

import matplotlib.pyplot as plt
import math
import numpy as np

Coordination

local coordination은 x축이 진행방향이고 right handed system이다.

In [2]: 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

def pltset():
    f, ax = plt.subplots()
    plt.grid()
    plt.xlim(-15,15)
    plt.ylim(-15,15)
    plt.axvline(x=0, color='y', linestyle='--', linewidth=3, alpha=0.5)
    plt.axhline(y=0, color='y', linestyle='--', linewidth=3, alpha=0.5)

def z_axis_transfrom_op(yaw, pos):
    
    cy = math.cos(yaw) 
    sy = math.sin(yaw)
    x = pos[0]
    y = pos[1]
    z = pos[2]

    return np.array([[cy, -sy, 0, x],
                      [sy, cy, 0, y],
                      [0, 0, 1, z],
                      [0, 0, 0, 1]])
In [3]: 
1
2
3
4
5
6
7
8
9
10
11
12

# plt setting    
pltset()

# plot
car_pos1 = np.array([0,0,0,1]).reshape(-1,1)
car_pos2 = np.array([1,0,0,1]).reshape(-1,1)
car = np.append(car_pos1, car_pos2, axis=1)
v = car[:,1] - car[:,0]

plt.scatter(car[0][0], car[1][0] ,s=150, marker='*', color='red')
# plt.scatter(car[0][1], car[1][1] ,s=50, marker='x', color='blue')
plt.quiver(car[0][0], car[1][0], v[0], v[1], color=['red'], scale=10)

1

<matplotlib.quiver.Quiver at 0x7f7b6dde2ac8>

png

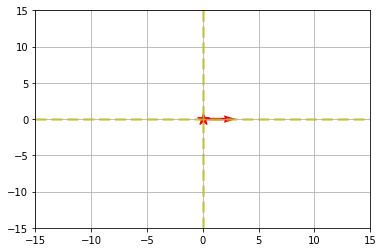
Robotic에서 많은 경우에 위의 경우와 같이 Local 좌표계에서
북쪽을 x축 기준으로 하며 yaw를 북측기준 시계방향으로 설정한다.
우선 변환 matrix를 나타내보자. 현재의 frame을 {A}라고 하고 변환 후의 frame을 {B}라고 하자.

frame 변환 matrix는 다음과 같이 나타낼 수 있다.

\[_{A}^{B}T = \begin{bmatrix} _{A}^{B}R & _{AORG}^{B}P \\ 0 & 1 \\ \end{bmatrix} = \begin{bmatrix} cos\phi & -sin\phi & 0 & x \\ sin\phi & cos\phi & 0 & y \\ 0 & 0 & 1 & z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\]

$_{A}^{B}T : ^{A}P \rightarrow ^{B}P$ 는 z축으로 90도 회전하는 변환이며 아래와 같이 표현된다.
\(_{A}^{B}T = \begin{bmatrix} 0 & -1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\)

In [4]: 
1
2
3
4
5
6
7
8
9
10
11
12
13

# plt setting 
pltset()

# plot
yaw = math.pi / 2
a_trans_b = z_axis_transfrom_op(yaw, car[:,0])
local_car = np.matmul(a_trans_b,car)

v = local_car[:,1] - local_car[:,0]

plt.scatter(local_car[0][0], local_car[1][0] ,s=150, marker='*', color='red')
# plt.scatter(car[0][1], car[1][1] ,s=50, marker='x', color='blue')
plt.quiver(local_car[0][0], local_car[1][0], v[0], v[1], color=['red'], scale=10)

1

<matplotlib.quiver.Quiver at 0x7f7b6d6aada0>

png

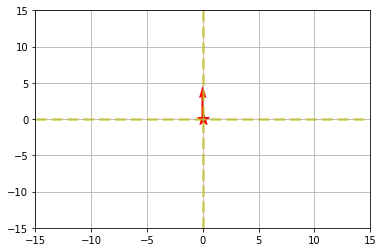
위 그림은 local 좌표계를 나타낸다.

Local 에서 Global 으로의 변환

local coordination을 B frame이라고 하고,
global coordination을 C frame이라고 하자.
이 때, B frame에서 C frame으로 변환해보자.

A frame에서 차가 갖고있는 위치정보는 다음과 같다고 하자. \(yaw(\phi) = \frac{\pi}{6} \\ \mbox{global position} = \begin{bmatrix} 8 \\ 5 \\ 0 \\ 0 \\ \end{bmatrix}\)

위에 나타나 있는 A frame 정보를 사용하면 \(\\_{A}^{C}T = \begin{bmatrix} cos\frac{\pi}{6} & - sin\frac{\pi}{6} & 0 & 8 \\ sin\frac{\pi}{6} & cos\frac{\pi}{6} & 0 & 5 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\)

local 좌표에서 global 좌표로 변환하려면 $-\frac{\pi}{2}$ 만큼 회전하고 다시 $\frac{\pi}{6} $ 만큼 회전하고 $(8,5,0)$ 만큼 이동을 하면 된다.

이것을 수식으로 나타내면 다음과 같다.

B에서 C frame으로 변환시 B에서 A 로 변환을 하고 A에서 C 로 변환을 해야한다. 아는 변환식을 사용해 표현하면,
\({}_{B}^{C}T = {}_{A}^{C}T_{B}^{A}T = {}_{A}^{C}T({}_{A}^{B}T)^{-1}\) 임의의 yaw = $\phi$ 와 global position = $(x,y,z)$ 에대해서 위의 변환식을 풀면 아래와 같다. \({}_{B}^{C}T = \begin{bmatrix} cos\phi & - sin\phi & 0 & x \\ sin\phi & cos\phi & 0 & y \\ 0 & 0 & 1 & z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} 0 & 1 & 0 & 0 \\ -1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} = \begin{bmatrix} sin\phi & cos\phi & 0 & x \\ -cos\phi & sin\phi & 0 & y \\ 0 & 0 & 1 & z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\)

In [5]: 
1
2
3
4
5
6
7
8
9
10
11
12

pltset()

yaw = math.pi/6
car_pos = np.array([8,5,0]).reshape(-1,1)
a_trans_c = z_axis_transfrom_op(yaw, car_pos[:,0])
b_trans_c = np.matmul(a_trans_c, np.linalg.inv(a_trans_b))
global_car = np.matmul(b_trans_c, local_car)
v = global_car[:,1] - global_car[:,0]

plt.scatter(global_car[0][0], global_car[1][0] ,s=150, marker='*', color='red')
# plt.scatter(global_car[0][1], global_car[1][1] ,s=50, marker='x', color='blue')
plt.quiver(global_car[0][0], global_car[1][0], v[0], v[1], color=['red'], scale=10)

1

<matplotlib.quiver.Quiver at 0x7f7b6d6289b0>

png

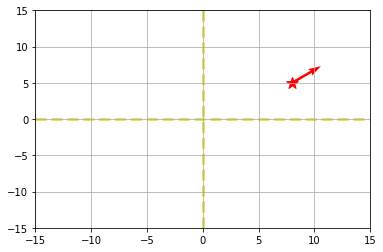
Robotic에서 많은 경우에 Global 좌표계에서
북쪽을 x축 기준으로 하며 yaw를 북측기준 시계방향으로 설정한다.
따라서 현재의 frame을 {C}라고 하고 변환 후의 frame을 {D}라고 하자.

$_{C}^{D}T : ^{C}P \rightarrow ^{D}P$ 의 변환은
z축으로 90도 회전하는 변환이며 아래와 같이 표현된다.

\[_{C}^{D}T = \begin{bmatrix} 0 & -1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\]

역변환을 구하는 방법은 아래와 같다. \(_{B}^{A}T = (_A^BT)^{-1} = \begin{bmatrix} (_{A}^{B}R)^{T} & -(_{A}^{B}R)^{T}{}_{AORG}^{B}P \\ 0 & 1 \\ \end{bmatrix}\)

local frame 인 {B} 에서 global frame인 {D}로의 변환은 \(_{B}^{D}T = _C^DT _A^CT (_A^BT)^{-1} = _{C}^{D}T _{B}^{C}T = \begin{bmatrix} 0 & -1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} sin\phi & cos\phi & 0 & x \\ -cos\phi & sin\phi & 0 & y \\ 0 & 0 & 1 & z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} = \begin{bmatrix} cos\phi & -sin\phi & 0 & -y \\ sin\phi & cos\phi & 0 & x \\ 0 & 0 & 1 & z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\)

In [6]: 
1
2
3
4
5
6
7
8
9
10
11

pltset()

car_pos = np.array([0,0,0]).reshape(-1,1)
yaw = math.pi / 2
c_trans_d = z_axis_transfrom_op(yaw, car_pos[:,0])
global_car = np.matmul(c_trans_d, global_car)
v = global_car[:,1] - global_car[:,0]

plt.scatter(global_car[0][0], global_car[1][0] ,s=150, marker='*', color='red')
# plt.scatter(global_car[0][1], global_car[1][1] ,s=50, marker='x', color='blue')
plt.quiver(global_car[0][0], global_car[1][0], v[0], v[1], color=['red'], scale=10)

1

<matplotlib.quiver.Quiver at 0x7f7b6d65bac8>

png

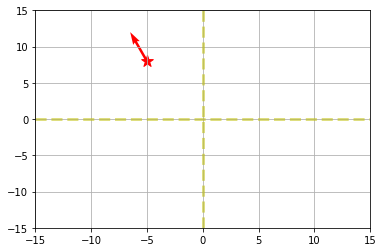
Global 에서 Local로 변환

$_{D}^{B}T : ^{D}P \rightarrow ^{B}P$ 의 변환은

$_{B}^{D}T : ^{B}P \rightarrow ^{D}P$ 의 변환의 역변환이므로

\[_{D}^{B}T = _{B}^{D}T^{-1} = (_{C}^{D} T _{B}^{C}T)^{-1} = \begin{bmatrix} \begin{bmatrix} cos\phi & sin\phi & 0 \\ -sin\phi & cos\phi & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} & -\begin{bmatrix} cos\phi & sin\phi & 0 \\ -sin\phi & cos\phi & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} -y \\ x \\ z \\ \end{bmatrix} \\ \begin{bmatrix} 0 & 0 & 0 \end{bmatrix} & 1 \end{bmatrix} \\ =\begin{bmatrix} cos\phi & sin\phi & 0 & ycos\phi-xsin\phi \\ -sin\phi & cos\phi & 0 & -ysin\phi-xcos\phi \\ 0 & 0 & 1 & -z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\]
In [7]: 
1
2
3
4
5
6
7
8
9
10
11

pltset()
car_pos = np.array([0,0,0]).reshape(-1,1)
yaw = math.pi / 2
b_trans_d = np.matmul(c_trans_d, b_trans_c)
d_trans_b =  np.linalg.inv(b_trans_d)
local_car = np.matmul(d_trans_b,global_car)
v = local_car[:,1] - local_car[:,0]

plt.scatter(local_car[0][0], local_car[1][0] ,s=150, marker='*', color='red')
# plt.scatter(local_car[0][1], local_car[1][1] ,s=50, marker='x', color='blue')
plt.quiver(local_car[0][0], local_car[1][0], v[0], v[1], color=['red'], scale=10)

1

<matplotlib.quiver.Quiver at 0x7f7b6d584a90>

png

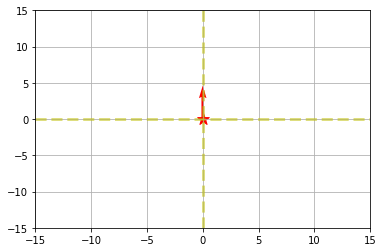
다시 원래의 좌표로 돌아오는 것을 알수 있다.
위와 같은 변환 행렬을 통하면 point cloud를 한번에 변환할 수 있다.

point cloud의 변환

다수의 point를 한번에 transformation matrix를 통해서 효과적으로 옮겨보자.

point cloud의 local 에서 global로 변환

In [8]: 
1

import math
In [9]: 
1
2
3
4
5
6
7
8
9
10
11
12

def local_to_global_matrix(location, yaw):
    x,y,z = location[0], location[1], location[2]    
    cy = math.cos(yaw) 
    sy = math.sin(yaw)
    x = location[0]
    y = location[1]
    z = location[2]

    return np.array([[cy, -sy, 0, -y],
                      [sy, cy, 0, x],
                      [0, 0, 1, z],
                      [0, 0, 0, 1]])
In [10]: 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

plt.cla()
plt.grid(linestyle='--')  
plt.axvline(x=0, color='y', linestyle='--', linewidth=3, alpha=0.5)
plt.axhline(y=0, color='y', linestyle='--', linewidth=3, alpha=0.5)
plt.axis("equal")

location = [15,17,0]
yaw = math.pi*1/3

f = lambda x: np.sqrt(np.cos(x)) * np.cos(80 * x) + 0.5 * np.sqrt(abs(x))
x = np.linspace(-math.pi/2, math.pi/2, 1000)
y = f(x)
plt.plot(x,y, color='red')

l2g_matrix = local_to_global_matrix(location, yaw)
x = x.reshape(1,-1)
y = y.reshape(1,-1)
local_location = np.concatenate([x,y,np.zeros_like(x),np.ones_like(x)],axis=0)
global_location = np.matmul(l2g_matrix,local_location)
plt.plot(global_location[0,:],global_location[1,:], color='red')

1

[<matplotlib.lines.Line2D at 0x7f7b6d4fa9b0>]

png

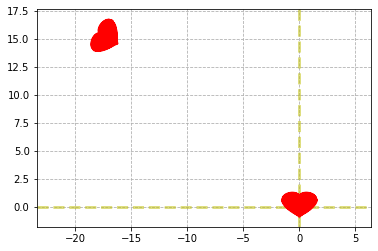
point cloud의 global 에서 local로 변환

In [11]: 
1
2
3
4
5
6
7
8
9
10
11
12

def global_to_local_matrix(location, yaw):
    x,y,z = location[0], location[1], location[2]    
    cy = math.cos(yaw) 
    sy = math.sin(yaw)
    x = location[0]
    y = location[1]
    z = location[2]

    return np.array([[cy, sy, 0, y * cy - x * sy],
                      [-sy, cy, 0, -y * sy - x * cy],
                      [0, 0, 1, z],
                      [0, 0, 0, 1]])
In [12]: 
1
2
3
4
5
6
7
8
9
10
11
12

plt.cla()
plt.grid(linestyle='--')  
plt.axvline(x=0, color='y', linestyle='--', linewidth=3, alpha=0.5)
plt.axhline(y=0, color='y', linestyle='--', linewidth=3, alpha=0.5)
plt.axis("equal")
plt.plot(global_location[0,:],global_location[1,:], color='red')

g2l_matrix = global_to_local_matrix(location, yaw)
x = x.reshape(1,-1)
y = y.reshape(1,-1)
restored_local_location = np.matmul(g2l_matrix, global_location)
plt.plot(restored_local_location[0,:],restored_local_location[1,:], color='red')

1

[<matplotlib.lines.Line2D at 0x7f7b6cfdc4e0>]

png

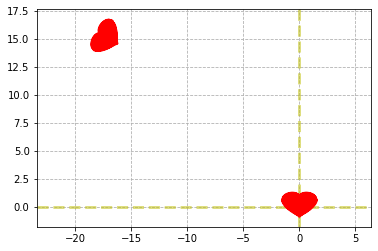
Leave a comment

You may also enjoy

Reeds-Shepp (RS) Path

18 minute read

이동체의 운동 구속조건을 반영하면 전진과 후진 경로에 대한 48가지 경로의 조합을 체크하는 RS path를 배워보자.

Model Predictive Control (MPC)

17 minute read

motion model로 다음 상태를 예측하여 비용함수를 만들고 모델을 제약사항으로 최적화를 하여 제어값을 찾아내는 MPC에 대해서 배워보자

RRT star

15 minute read

RRT star 알고리즘에 대해서 알아보자.