APM part2

Contents

NP Complete

Approximation

Approximation Technique

DM, ML Algorithm

NP Complete

Definition

Definition of P

질문자체에 대해서 예 혹은 아니오로 다항식 시간안에 답할 수 있는 문제

The class of problems that can be decided in polynomial time

Definition of NP

예라는 근거가 주어졌을 때 그것이 Yes임을 다항식 시간안에 확인 할 수 있는 문제

1. Set of decision problems so that for any yes instance, it has a verifiable proof so that with the proof, one can be verify that the instance is yes in a polynomial time by a Turing machine.
2. Set of decision problems that can be solved by a Non-deterministic TM (NTM) in a polynomial time of the input bit size.

Definition of NP-hard

Np-hard는 이 집합에 속한 문제들 대해서 서로 다항식 시간 변환¹이 가능한 문제 집합이다.

If we could solve this problem in polynomial time, we could solve all NP problems in polynomial time

Definition of NP-Complete

Np 이고 Np hard 를 만족하는 문제. 따라서, 이중 하나의 문제라도 polynomial time안에 풀린다는 것을 증명하면 Np-hard에 속한 모든 문제가 polynomial time안에 풀린다.

풀어서 말하면, 지금까지의 기술로는 다항시간에 풀기 어렵다고 판단되면서, 서로 밀접한 논리적 연결관계를 가진 문제들의 집합이다.

왜 중요한가? 어떤 문제의 최적해와 유사한 decision version(Yes or No question)에 대한 문제를 푸는 알고리듬을구하면 그 문제와 reduction 할 수 있는 문제도 풀수 있게 되므로, 최대한 많은 NP complete 연결고리를 찾는 것이 좋다.

The set of NP-complete problems are all problems in the complexity class NP for which it is known that if any one is solvable in polynomial time, then they all are.

conversely, if any one is not solvable in polynomial time, then none are.

SAT

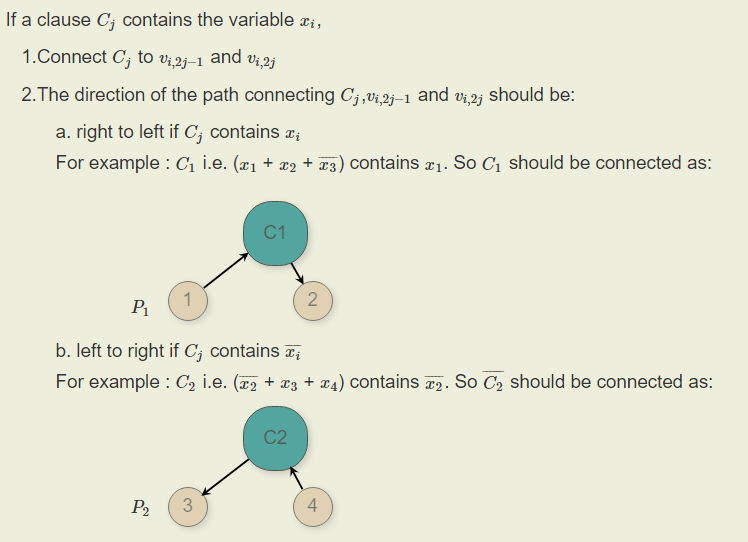
Problem: 논리곱 정규형(CNF(Nonjunctive Normal Form))의 부울 식이 주어졌을 때 그 식을 만족하는 변수를 찾는 문제

Cook-Levin Therom

SAT 문제는 NP complete이다.

3-SAT is NP: Since for any yes instance (satisfiable CNF formula), there is a proof (satisfying assignment) so that with this proof a polynomial time algorithm (that checks whether the given assignment makes the CNF formula to be true) can confirm that the instance is a yes case.

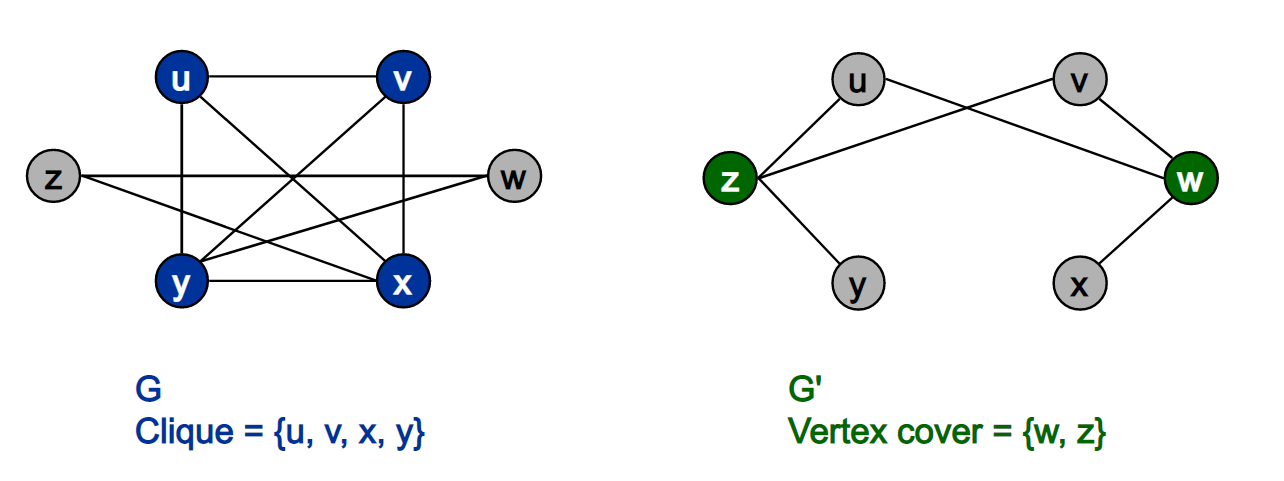
Clique

Problem: undirected 그래프 $G = (V,E)$ 에서 size $k$짜리 Clique² 가 존재하는가

**Clique is NP: ** clique인 subgraph에서 모든 pair의 vertices가 연결이 되어있는가 $O(N^2)$ 안에 확인 가능 (vertice 수를 $N$ 이라 하면) **Clique is Np-hard 증명 그림 및 detail **

일단, NP-hard 집합의 개념 이해 필요! NP-hard 어떤 문제를 polynomal 안에 풀수 있다면(진짜 풀 수있는지는 모름), (NP-hard 안의 모든 문제들 사이에서 polynomial time 안에 변환이 가능해서)NP-hard안에 있는 모든 집합의 문제들이 전부 polynomial 안에 풀릴 수 있는 문제들의 모임.

if 3-SAT $\le_p$ Clique (3-SAT is reducible to Clique), Clique is NP-hard (3-SAT 는 어려운 문제고, reduction algorithm 에 의해 3-SAT를 Clique로 변환가능한데, 이게 만약 polynomial 안에 풀리면, 3-SAT, Clique 모두 polynomial time안에 풀 수 있는 것임). 따라서, polynomial reduction 알고리즘과 $\Leftrightarrow$ 관계를 설명해야 함

Reduction algorithm: 어떤 한 3-SAT인 boolean equation $\Phi$ 가 주어졌을때, 각각의 literal 에 대해서 vertex를 만들고, 자기가 속한 clause의 literal과 다른 clause에서의 negation을 제외한 나머지 에 대해서 edge를 만든다. ($\Phi$ 안에 총 m 개의 clause가 있다면 m개의 cluster가 생김). 이 과정은 $O(N^p)$ 걸림.

(여기서 알수있는 intuition은 각 생성된 graph의 vertex가 연결되 있다면, 그에 대응하는 literal 쌍은 동시에 True)

3-SAT $\Rightarrow $ k-Clique: 3-SAT가 satisfiable하면(각 clause 마다 적어도 하나의 literal이 True, 게다가 negation은 연결하지 않았음), (각기 다른 clause 에서 파생된 vertex는 반드시 연결되어 있기 때문에) clause의 수(m=k) 사이즈의 clique가있을 수 밖에 없다.

k-Clique $\Rightarrow$ 3-SAT: k-Clique가 그래프에 있다면, (k개의 cluster에서 하나씩의 vertex가 연결이 되어 있어서 그에 대응되는 clause의 literal이 모두 True가 되므로)모든 clause는 True가 되어 $\Phi$는 satisfiable하다.

Independent Set

Problem: undirected graph $G$ 에서 size $k$ 짜리 IS³ 가 존재하는가

**IS is NP: ** IS set에서 모든 pair의 vertices가 연결이 되어있는가 $O(V^2)$ 안에 확인 가능

IS is Np-hard 증명

Reduction algorithm: graph $G = (V, E)$ 가 주어졌을때, graph의 edge에 대해 complement 연산을 수행하면

$\bar{G} = (V, \bar{E})$ 가 되는데 이 연산은 모든 vertex pair에 대해 edge가 존재하는지 확인하고 있다면 삭제하고, 없으면 새로 edge를 만드는 작업이므로 $O(V^2)$ 이 걸림

Clique $\Rightarrow $ IS: clique set 이 size $k$ 짜리 $A$ 라고 하고, graph를 complement를 했을때, $A$ 의 원소인 vertex들 사이의 edge가 존재하지 않으므로 $A$ 는 size $k$ 짜리 IS가 됨

IS $\Rightarrow $ Clique: IS set 이 size $k$ 짜리 $A$ 라고 하고, graph를 complement를 했을때, $A$ 의 원소인 vertex들 사이의 edge가 항상 존재하므로 $A$ 는 size $k$ 짜리 clique가 됨

Vertex Cover

Problem: undirected graph $G$ 에서 size $k$ 인 Vertex Cover⁴가 존재하는가에 대한 문제

**Vertex Cover is NP: ** size $k$ 의 VC $V’$가 주어지면, graph $G$ 의 모든 edge $(u,v)$ 마다 $V’$안에 $u,v $ 둘중 하나가 포함되어있나 확인, 따라서, polynomial time 이 걸린다. naive한 알고리즘의 예로, $O(EV’) = O(EV)$

#given G.E, V' in VC set,
for (u,v) in G,E 
	for k in V' 
		if k == u or k == v 
			pass
        else 
        	return False
return True 

Vertex Cover is Np-hard 증명

Reduction algorithm: graph $G = (V, E)$ 가 주어졌을때, graph의 edge에 대해 complement 연산을 수행하면

$\bar{G} = (V, \bar{E})$ 가 되는데 이 연산은 모든 vertex pair에 대해 edge가 존재하는지 확인하고 있다면 삭제하고, 없으면 새로 edge를 만드는 작업이므로 $O(V^2)$ 이 걸림

Clique $\Rightarrow $ VC: 주목할점: $k-clique \Rightarrow

V

-k$ size 의 $VC$

만약 주어진 graph $G$ 에 $k-clique$ set $A \sub V$와 graph의 complement 연산을 한 $\bar{G}$ 가 있다고 하자.

만약 $(u,v) \in \bar{E}$ 이면, $u,v$ 둘중 하나는 반드시 $V-A = V’$ 에 속한다.

(왜냐하면 $(u,v) \notin E $이면 $u,v$ 둘중 하나는 반드시 $V-A$에 속하기 때문이다.)

따라서, $V’$ set 이 Vertex Cover set이 되고, size는 $

V

-k$ 짜리 가 된다.

VC $\Rightarrow $ Clique: 주목할점: $

V

-k$ size 의 $VC$ $\Rightarrow k-clique$

만약 $u,v \notin V’$ 이면, complement를 하면 $(u,v)\in E$ 가 반드시 존재하므로 $V-V’= A$는 Clique set 이다.

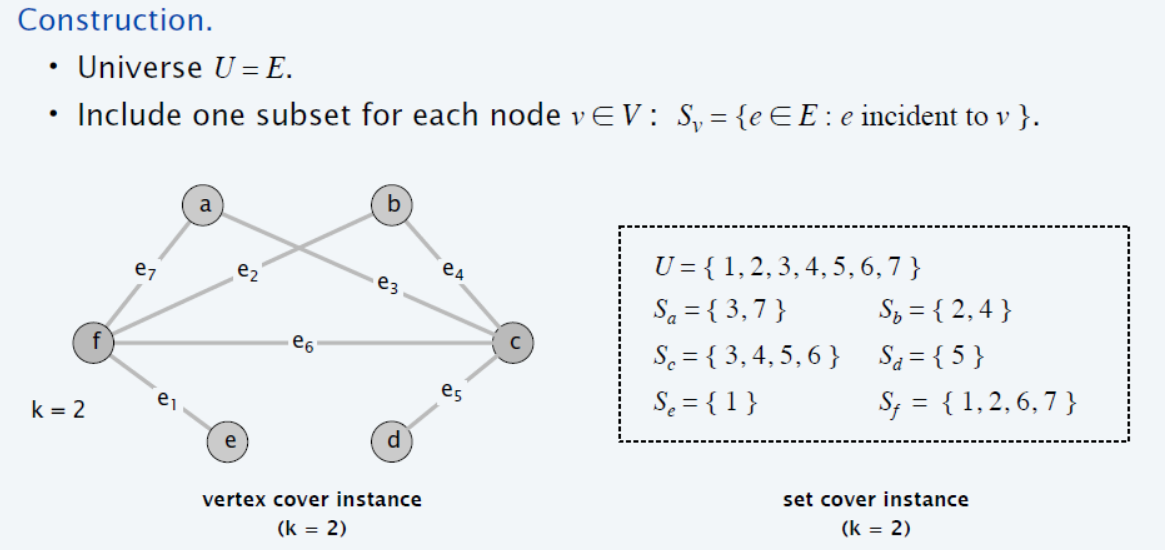
Set Cover

Problem: 말 보다 수식으로 표현하는게 더 쉽다.
\(U \supset C \supset C'\text{with size k } \\ \text{FIND } C'\text{s.t } \underset{S_i \in C'}{\cup}S_i = U\) SC is NP: naive 하게 생각해보면 주어진 $C’$를 가지고 $\underset{S_i \in C’}{\cup}S_i = U$ 이 되는지 확인하면 된다. $U$에 있는 모든 원소수가 $n$ 개라고 가정하고, 집합 $C’$의 원소 집합 $S_*$수를 m개 라고하면 $O(nm)$이므로 polynomial time이 걸림

SC is NP-hard

Reduction algorithm:

size $k$ 짜리 Vertex Cover instance가 undirected graph $G =(V, E)$에 있을때, 이를 어떻게 Set Cover 문제로 바꾸고, 어떤 instance를 만드는지에 대해 설명하겠다.

Set Cover에서 커버할 모든 원소는 graph $G$의 모든 edge $E$로 한다. 따라서, 커버할 set $U = E$가 됨.

또, $C’$ 의 각 원소집합 $ S_i $는 graph $G$에서 $v_i$ 에 incident한 edge들로 구성된다.

($G$에서 전체 edge $G.E = U$로 만들고, 각각의 vertex마다 incident한 edge를 check하여 set $F={S_v}

_{v \in G.V}$를 만드는것은 모든 vertex 마다 incident edge를 체크해야하는데, edge하나당 vertex 는 2개 연결되어있으므로 naive 하게 생각하면 $O(2

E

)$ 시간 필요. 따라서, polynomial time이 걸림 )

이렇게 변환된 Set Cover 문제의 size $k$는 Vertex Cover size $k$ 와 동일하다. (왜 그런지는 증명을 보면 됨)

VC$\Rightarrow $ SC: VC set의 정의는 모든 edge 에서 한쪽 정점은 반드시 VC set에 걸쳐 있다. 따라서 Vertex Set에 속한 k 개의 정점들 $v_i

_{i=1,..,,k}$에 대해 대응된 k개의 $S_i

_{i=1,..,k} = C’$ 들만 골라서 union하면 모든 edge 원소들 A를 커버하게 된다.

SC $\Rightarrow $ VC: Set Cover의 instance에서 A를 cover하는 k개의 $S_i

_{i=1,..,k} = C’$에 대응된 vertex들 $v_i

_{i=1,..,,k}$ 집합이 VC set 을 이룬다. 왜냐하면 $S_i

_{i=1,..,k} = C’$ 가 A를 커버한다는것은 모든 edge E를 커버한다는 것이고, $S_i$ 는 $v_i$에 incident 한 vertex set으로 이루어졌으므로, $v_i

_{i=1,..,,k}$ 역시 모든 edge를 커버하기 때문에, edge에서 정점 2개중 하나는 반드시 $v_i

_{i=1,..,,k}$에 포함된다.

Set Sum

Hamiltonian Path

Problem: directed graph.에서 모든 vertices 를 한번씩만 방문하는 path(Hamiltonian path)가 있는가 (cycle도 비슷하다.)

**HAMPATH is NP: **어떤 graph에서 HAMPATH 가 주어지면, 그것은 서로 다른 vertex sequence인데, 각각의 연속된 정점 간의 edge 가 graph에 있는지 확인하는데 polynomial time이 걸린다.

Check if every vertex (except the first) appears exactly once, and that consecutive vertices are connected by a directed edge

Ham-Path is NP-hard

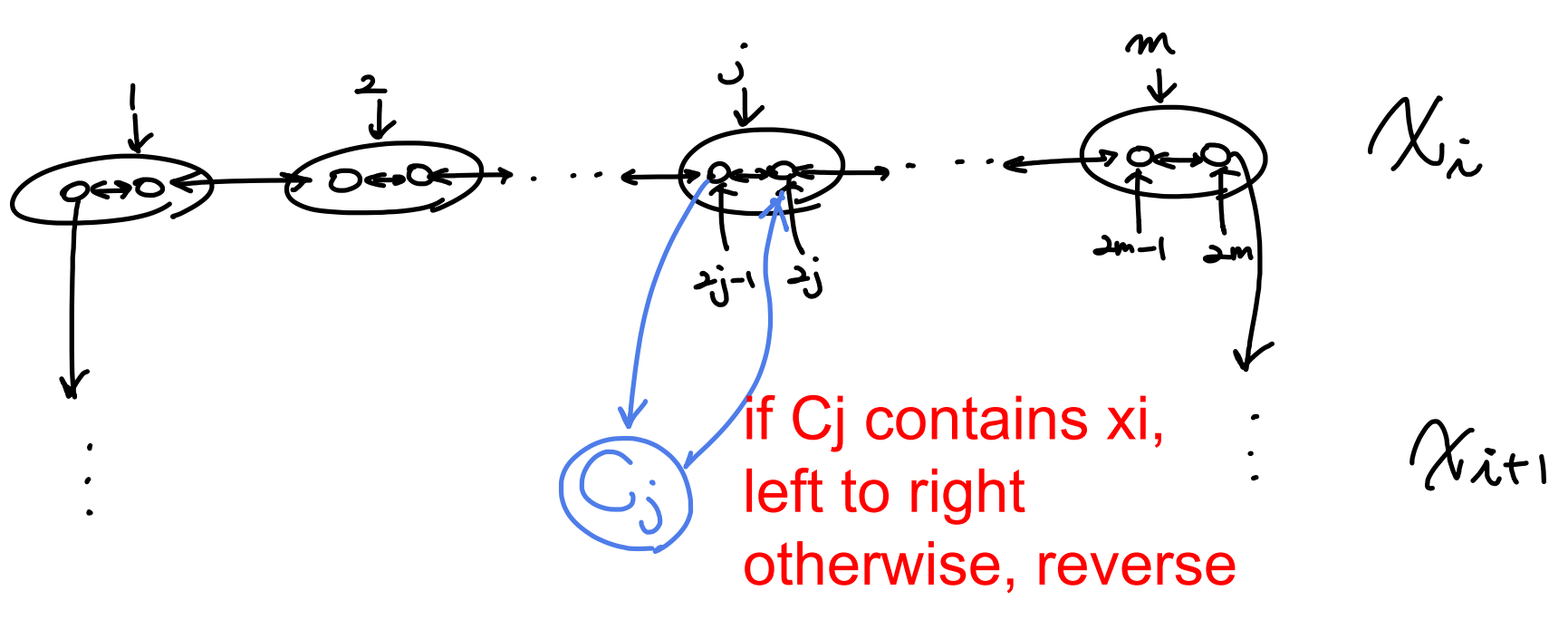
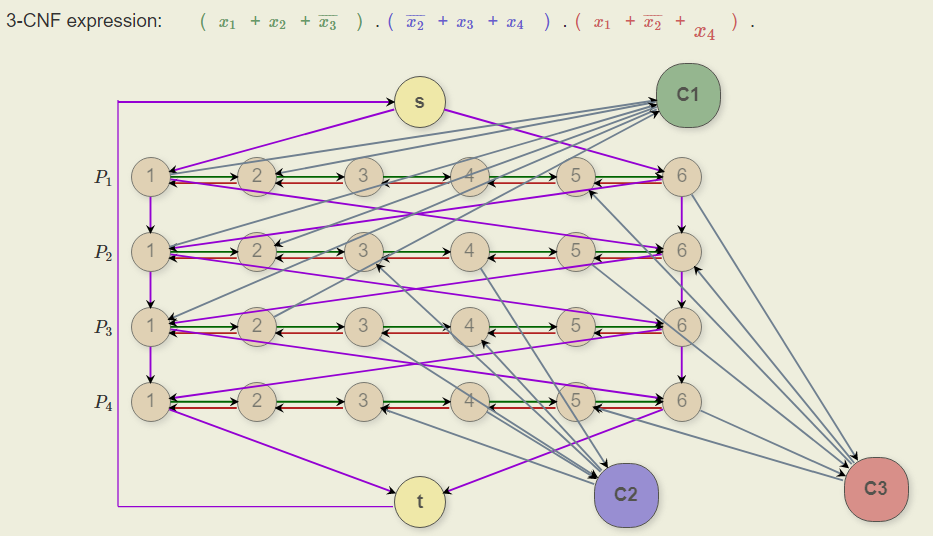
Reduction algorithm: 3-SAT의 literal $x_1, .., x_n$에 대해서m 개의 clause가 있었다면, 각 literal마다 $2m$ 개의 정점들로 구성된 양 방향 horizontal path를 만들고, literal 순서대로 양끝을 이어 나간다.

그 후에, 각 clause 마다 정점을 하나씩 만들고, 3-SAT에서 $x_i$ 가 True였다면 왼쪽에서 오른쪽으로, 아니였다면 반대로 path를 만든다.

따라서, 다음과 같이 완성

Ham-Path $\Rightarrow $ 3-SAT: 만약, hamiltonian cycle에서 $x_i$ 에대한 horizontal path가 왼쪽으로 오른쪽이었다면, $x_i$ 를 True로, 아니면 False로 assign한다면 Boolean 수식은 satisfiable하게 된다. 왜냐하면 hamiltonian cycle에서 각 clause에 대한 node를 한번씩 지나게 되는데 그 한번만 지날때의 horizontal path에서 literal이 clause를 True로 만들게 된다. 따라서, 모든 clause가 True가 되어 satisfiable하다.

3-SAT$\Rightarrow $ Ham-Path: 각 horizontal path에 대응하는 literal이 True였다면 왼쪽에서 오른쪽으로 path를 결정하고, 그게 아니면 오른쪽에서 왼쪽으로 결정한다면 결국에는 hamiltonian cycle이 된다.

영문 설명1 설명2

TSP

Problem: undirected complete graph $G$에서 가중치의 합이 $k$ 인 TSP⁵ 가 존재하는가의 유무

TSP is NP: $V$ 개의 정점 sequence(cycle에서 마지막 정점 제외)가 주어지면, 각 정점이 1번 등장하는지 우선 체크하고, edge weight의 합이 $k$ 가 되는지도 체크 한다.(Hamiltonian Path 때와 비슷하게 consecutive하게 체크)

TSP is NP-hard

Reduction algorithm: Hamiltonian Cycle 을 가진 directed graph $G = (V,E)$를

TSP instance 를 가진 undirected complete weight graph $G’ = (V,E’)$ 로 바꿔야한다.

따라서, 모든 노드들간의 edge를 만들어주되, 원래 edge가 없는데 새로 만든것은 weight를 $1$ 아니면 $0$을 부여

그렇게 만들면, TSP instance의 $k$ 값을 $0$으로 하는 instance가 있는 graph $G’$을 만들 수 있다.

Q : (무향 완전 가중 그래프를 주며) 이 그래프에서 모든 노드들을 한번씩만 방문하고, 그 가중치의 합이 0인게 있어? (Decision version) \(E' = \{ (i,j): i,j \in V \and i \neq j \} \\ c(i,j) = \begin{cases} 0 &\text{if }(i,j) \in E \\ 1 &\text{if }(i,j) \notin E \end{cases}\)

Ham-Cycle $\Rightarrow $ TSP: Ham-Cycle이 있는 그래프 G에서 변형된그래프 G’에도 $k=0$인 TSP가 존재하기위한 intuition은 G에 없었는데 추가된 edge를 TSP에서 절대 지나면 안된다. 즉, 원래의 Hamiltonian cycle instance자체가 $k$가 $0$인 TSP가 된다.

TSP $\Rightarrow $ Ham-Cycle: $k=0$ 인 TSP 는 $E$ 상의 edge만 지나는 cycle이다. 따라서, 그 TSP가 곧 hamiltonian cycle instance가 된다.

한글 blog 설명

Approximation

NP complete 을 다루는 위해 문제 범위를 좁히기 위해 problem종류는

Optimization version, Decision version, Gap version problem이 있다.

또한, Algorithm은 Exact Algorithm 과 Approximation Algorithm 범주로 나뉜다.

Approximation 알고리즘에 사용되는 여러 technique들이 있다.

Approximate Ratio: $\rho \ge max(\frac{C^}{C}, \frac{C}{C^}) \ge 1$

approximation algorithm이 exact algorithm에 비해 최대 얼마정도의 비율로 garantee 하는가를 알 수 있다.

일반적으로 $\rho$-* algorithm 으로 사용

PTAS, FPTAS

PTAS: Ploynomial-time approximation scheme. Input size $n$ 에 ploynomial 하다.

하지만, 어떤 요소 $\epsilon$ 에따라 exponential 해지는 요소가 있다.

FPTAS: Fully polynomial-time approximation scheme. Input size $n$ 에 ploynomial 하다.

하지만, 어떤 요소 $\epsilon$ 에따라 반비례하여 증가하는 요소가 있다.

Vertex Cover

임의의 edge (u,v)를 선택하여 VC set에 추가하고, graph 에서 $(u,v)$ 와 incident 한 edge들을 제거한다.

VC(G)
	# Vertex Cover 
	create set C
    # helper set for Vertex Cover 
    create set E`
    E` ← G.E
    
    while E != {}
    	(u,v) ← pick one edge(E`)
    	C = C union {u,v} # vertex 2개씩 추가된다.
        remove from E` every edges incident on either u or v 
    return C 

adjacent list 를 사용했을때 모든 graph의 node와 edge를 봐야하므로 $O(V+E)$

python

2-approx algorithm proof

set $A$를 매iteration에서 $C$로 들어갈 vertex $u,v$로 이루어진 edge $(u,v)$들의 set 이라고하면

set $A$의 size는 $C$ size의 절반이다. (매 vertex가 2개씩 추가되는데 $A$는 edge set 이고, $C$는 vertex set 이니까) \(|C| = 2|A|\)

이때, $A$의 어떤 엣지라도 endpoint를 공유하지 않는다는 사실을 주목하자. 그러면 $A$의 어떤 2개의 edge 를 골라도 optimal vertex set $C^$ 에 있는 vertex 원소 하나에 의해 cover 되지는 않는다. (즉, A의 어떤 edge든지 적어도 그중 하나의 vertex는 $C^$ 의 원소에 있어야한다.) \(|C^*| \ge |A|\)

따라서, \(|C^*| \ge |A| \ge |C|/2 \\ \Leftrightarrow \rho=2 \ge |C|/|C^*|\)

Set Cover

PTAS approximation algorithm 의 범주에 속한다.

greedy choice를 통해 approximated solution을 구한다.

$U$의 원소들중 greedy choice는 커버되지 않고, 남은 원소들에 대해서 $F$ 의 원소 집합중 가장 많은 cover를 할수 있는 set 을 선택 하여 $C’$를 만들어 나간다.

notation \(\begin{aligned} U &= \{ e_1, e_2, ... e_m\} \\ F &= \{ S_1, S_2, ... S_n\} \\ S_i &= \{ \mbox{some elements}\} ~\forall i \end{aligned}\)

SC(U, F)
	# uncovered residual elements 
	R = U.copy() 
    # approximated set cover 
    C` = {}
    while R != {}
    	# greedy choice: select an S in F that maximizes |S union R|
        # 남은 element들을 최대로 cover할수있는 S 선택
        S = F[argmax([len(Si ∩ R) for Si in F])]
        R ← R - S 
        C` ← C` union {S}
    return C`

while 문이 반복되는 경우의 수는 $min(

U

,

F

)$

왜냐하면 $

U

$가 되는 경우는 cover 되는 원소가 매 iteration 마다 1개씩만 되는 최악의 경우고,

일반적으로 모든 element가 Set ${S_{i} }

_{i=1,..,

F

}$ 에 의해 cover가 되는 경우의 시간이 걸린다.

greedy choice를 하는데 걸리는 시간은 $O(

U

F

)$이므로

$\because$ $F$의 원소 $S_i$ 마다 $X$와union 해봐야하는데 $S_i$에 있는 원소의 최대수는 $

U

$

총 걸리는 시간은 $O(

U

F

min(

U

,

F

))$

python

**(ln

U

+1) - approx algorithm proof**

이 알고리즘이 끝났을때, 각 원소 $ x \in U $에 대한 cost는 다음과 같이 정의된다.

원소 $x$ 에 대해 $S_1,…, S_{i-1}$들이 Set Cover의 원소들로 선택된 이후, $S_i$ 에의해 처음 선택이 되었을 때의 cost $c_x$ \(c_x = 1/|S_i - (\underset{k=1,...,i-1}{\cup}{S_k})|\)

Notice that $|S_i − ( S_1 ∪ S_2 ∪ … ∪ S_{i−1})|$ is the number of elements covered for the first time by $S_i$ at $i$ th iteration

Let $c_x$ be the price allocated to element $x ∈ X$, that is covered for the first time at $ i $ th iteration.

전체 iteration 동안 cost $

C

= \sum_{x\in U}{c_x}$ 가 된다.

optimal case일 떄의 cost 를 $\sum_{S \in C^*} \sum_{x\in S}{c_x}$ 가 되고 $S_i$ 에도 포함되고, $S_j$ 에도 포함되는 element가 존재 할수 있으므로 (1)이 된다. 그런데 이때, $\sum_{x\in S}{c_x} \le \sum_{i=1,..|S|}{1/i}$ 즉, harmonic summation에 bounded 되어있으므로 (증명은 생략)
\(\begin{aligned} |C| &\le \sum_{S \in C^*} \sum_{x\in S}{c_x} & (1)\\ &\le \sum_{S \in C^*}\sum_{i=1,..|S|}{1/i} \\ &\le |C^*|\sum_{i=1,..|S|}{1/i} &\mbox{for } \underset{S \in F}{max}{(|S|)} \\ &\le |C^*|(ln(|S|) + 1 )\\ &\le |C^*|(ln(|U|) + 1 )\\ &\Leftrightarrow \rho= (ln(|U|) +1)\ge |C|/|C^*| \end{aligned}\)

$U$ 의 size가 커질수록 log scale로 approximation ratio가 좋지 않아지므로

PTAS 범주에 속하는 근사 알고리즘이다.

Set Sum

TSP

TSP problem 의 optimization problem에 대해서 special case 에 대해서 polynomial time 2 - approximation algorithm 을 구할 수 있다.

special 조건 : complete graph G의 edge들의 weight가 triangle inequality 를 만족하는 경우.

Intutition: MST를 이용하여 TSP의 solution을 approximation 한다.

MST의 모든 edge weight의 sum은 TSP의 path 에서 edge들의 weight sum 에 의해 lower bound 되어있다.

그런데, G가 triangle inequality 를 만족한다면, TSP의 cost는 MST 의 weight sum의 2배에 upper bound 된다. 이 성질을 이용하자

DFS를 이용하여 MST를 traversal 하여 한바퀴 도는 정점 sequence $P$를 찾은뒤에 $P$에서 preorder순으로 Euler tour⁶ list $T$가 곧 TSP의 approximation solution이 된다.

# G is undirected weighted complete graph
# G.E should satisfy trangular inequlity 
TSP(G) 
	M ← MST(G)
    P ← Euler tour traversal of M using DFS(G,s)  
	
    T = []
    for v in P
    	if v is first appearance in P 
        	T ← v
    
    # make a cycle
    T ← s 
    return T 

알고리즘은 2개의 subroutine으로 구성된다. 먼저 MST를 만드는 작업은 $O(ElogV)$로 polynomial 하고, DFS를 통한 Euler tour를 찾고, preorder를 찾아내어 $T$를 얻는 작업 역시 polynomial 하다.

naive code

2 - approximation proof \(\begin{aligned} |M| &\le |OPT| \\ |P| &= 2|M| \le 2|OPT| &\because \mbox{visit each edge twice}\\ |T| &\le |P| &\because \mbox{triangle inequality} \\ \therefore |T| &\le 2|OPT| \\ \Leftrightarrow \rho &= 2 \ge |T|/|OPT| \end{aligned}\)

Baker’s Algo for MIS

Approximation Algorithm for MIS(Maximum Independent Set) on Planar Graphs

Appox Technique

approximation algorithm을 design 하는데 유용한 2가지 technique

Randomization

Karger’s Algo for ST-Min Cut

non-negative undirected edge weight graph 에서 min cut을 random한 방식으로 찾는 알고리즘

Karger(G) 
	# O(EV^2(logV)^2) 
    for k = 1 to V^2logV
        # one iteration takes O(ElogV)
        while != two vertex remain
            pick random edge (x,y) in G.E with probability ∝ its edge weight
            # merge process 
            while(!∃shared vertex v such that x and y are connected to a vertex v)  
                sum weight of (x,v) and (y,v)
            merge x and y 

polynomial time이 걸리지만, 엄청 느린 알고리즘으로 min cut을 구했을때 제대로 구할 확률은 $1-o(1)$ 이다!

proof

$

C

$ 를 ST min cut에서의 crossing edge weight의 합이라고하자.

그리고 어떤 한 vertex $u$ 와 연결된 edge들의 합($

C

$)이

$u$에 연결된 모든 light edge들의 합(optimal mincut $

C^*

$)보다 같거나 크다 점을 주목하자.

즉, $

C^*

\le

C

= \sum_{e \in E, ~ u \in e}{

e

} $ 이다.

확장해서, u를 모든 vertex에 대해서 생각하면 $|V||C^|$ 는 모든 edge의 합의 2배 $2|E|$에 upper bound된다. \(|V||C^*| \le 2(\frac{1}{2}\sum_{u\in V} \sum_{e\in E, u \in e}{|e|}) =2|E| \\ |C^*|/|E| \le 2/|V|\) 그런데, $|C^|/|E|$ 가 의미하는 바는 어떤 edge가 mincut $C^*$에 포함될 확률을 의미한다.

따라서, $\mathbb{P}(e_1 \notin C^*) \ge 1 - 2/

V

$ 이 되고,

merge가 반복되며 마지막 2개 남은 vertex edge들의 weight가 crossing edge의 합임을 주목

위의 식을 이용하여 edge를 선택하여 2개의 vertex만 남을때까지 merge를 반복하는 동안 mincut에 포함될 edge들을 한번도 선택하지 않아 제대로된 mincut을 찾을 확률의 bound를 찾도록 하겠다. 이 말은 즉슨, $

C^*

$를 찾는데 실패할 확률에 대한 bound를 구하겠다는 뜻.

($|V| = n$으로 두자) $$ \begin{aligned} &\mathbb{P}(e_1 \notin C^) \ge 1 - 2/n
&\mathbb{P}(e_2 \notin C^ |e_1 \notin C^) \ge 1 - 2/(n-1)
&\mathbb{P}(e_{n-2} \notin C^ | \and_{j=1,2,..,n-3} e_{j} \notin C^) \ge 1 - 2/3
\times&——————-
&\mathbb{P}( \and_{j=1,2,..,n-2} e_{j} \notin C^) \ge \Pi_{j=1,..,n-2}(1-2/(n-j+1)) \ge 2/(n(n-1)) \ge 2/n^2 \

\therefore \mathbb{P}&(\mbox{이 알고리즘이 iteration 한번동안 mincut에 실패할 확률}) \le 1 - 2/n^2 \
\mathbb{P}&(.. k번 시행) \le (1-2/n^2)^k \

&\mbox{ when }k = n^2logn,
\mathbb{P}&(.. n^2logn 번 시행) \le (1-2/n^2)^{n^2logn} = (1-2/n^2)^{(n^2/2)2logn} = o(1)

\end{aligned} $$

따라서, mincut이 성공할 확률이 $1$에 가까워지는것을 증명함

wiki

Linear Programming

Goemans Willianson Algo for Max Cut

MAX CUT problem with SDP relaxation

DM, ML Algorithm

PageRank

M 은 column stochastic matrix⁷ 이어야함

google pagerank 의 sparse matrix formulation version 을 power iteration을 통해 구한다.

풀고자하는 수식

($\delta:$ teleport probability[^8]) $$ \begin{aligned} r &= Ar
A &= \delta M + (1-\delta)[1/N]_{N} \

\because r &= \delta Mr + (1-\delta)[1/N]{N \times N}~ r
& = \delta M + (1-\delta)[1/N]{N} &\because \sum_i r_i = 1

\end{aligned} $$

PageRank(M, delta=0.8, elipslon=1e-8)
    N = M.shape[0]
    R = np.ones((N,1))*(1/N)
    K = np.ones((N,1))*((1- delta)/N)
    iteration = 0
    distance = INF

    while distance > elipslion:
        prevR = R
        R = delta * np.matmul(M,R) + K
        iteration = iteration + 1
        # L1 norm(euclidean distance)
        distance = np.linalg.norm(R-prevR)

    return R 

python

spider trap를 없애고, dead end 효과를 완화시키기 위해 사용됨

Power Iteration, PCA, SVD, CUR decomposition

Power iteration 을 통한 PCA(Principal Component Analysis)

$v_t = (M/

Mv_{t-1}

)v_{t-1}$ 을 수렴할때까지 power iteration을 통해 계산하면

highest eigen value를 가진 eign vector (즉, principal component)를 얻을 수 있다.

또한 $M = M - \lambda v v^T$ 와 같은 Gram schmidt process를 통해 PC 성분을 제거 후,

두번째로 높은 eigen value를 가진 eigen vector를 구할 수도 있다.

Power iteration python

PCA, SVD python

1. 다항식 시간 변환은 변환이 다항식 시간안에 이루어지고 두 사례의 답의 존재성(Yes or No)이 일치하는 문제이다 ↩

2. 그래프에서 어떤 pair의 vertices 라도 connected 되어 있는 sub graph의 vertex set ↩

3. IS(Indpendent Set)의 정의는 graph $G$ 가 주어졌을때, 서로간의 edge가 전혀 없는 vertex set (Clique의 반대) ↩

4. undirected 그래프에서 모든 간선의 양 끝점을 포함하는 정점들의 집합들 중 최소의 집합(optimal vertex cover)을 찾는 것. 즉, 어떤 edge를 선택하더라도, edge pair중 적어도 하나의 vertex가 포함되도록 하는 집합 ↩

5. Traveling salesman Problem 으로 complete graph 에서 edge를 weight sum를 최소로하는 hamiltonian cycle을 찾는 것이 optimization problem이고, decision version problem은 edge의 가중치의 합이 k hamiltonian cycle이 존재하는가의 문제 ↩

6. Eulerian trail (or Eulerian path) is a trail in a finite graph that visits every edge exactly once ↩

7. 각 열의 합이 1 인 행렬. 가장 큰 eigen value는 항상 1이다. 따라서, 매 iteration마다 normalize할 필요 없다. ↩