Adversarial Imitation via Variational Inverse Reinforcement Learning
지난포스트 AIRL의 후속논문인 EAIRL 논문을 가져왔다. 2019 ICML에 등재된 논문이다. 두 논문 모두 expert demonstration으로 부터 dynamics의 변화에 robust한 reward 함수를 복원하는데 초점이 맞추어져 있다. 실제 로봇의 보행 (ambulation) 과제에서 AIRL을 적용했을 때 발생하는 문제점에 대해서 다루고 있다. 아래의 글을 읽기전에 다음과 같은 두 포스트를 먼저 읽어보고 이글을 읽는 것을 추천한다.
Abstract
기존의 maximum entropy inverse reinforcement learning 의 formulation에 empowerment regularization 기법을 도입하여 문제를 풀었다. 그결과 expert demo로 overfitting되는 것을 막고 testing과 training상황이 조금 바뀌더라도 general하게 적용할수 있는 robust reward를 복원할 수 있다고 한다. 여기서 그 robust 함은 empowerment 를 정의하여 학습했기 때문이라 했고, empowerment는 reward와 policy사이의 variation information이라고 한다. 그것을 maximize하도록하여 학습을 했다고 한다.
\[\require{cancel}\]Contents
1. Introduction
IL은 BC를 통해 풀수있는데 이때 training 과 testing사이의 차이에서 발생하는 covariance shift로 compounding error가 누적되어서 한계점을 보였다. 그래서 GAIL에서는 Maximum causal entropy IRL framework 하에서 IL을 유도한 결과 GAN과 같은 구조로 Adversarial하게 효과적으로 reward와 policy를 동시에 학습할 수 있는 연결점을 찾았다. 이전포스트를 보면 previous work들과의 연결점을 알 수 있다. expert demo와 rollout data를 mix하여 학습하는 GAIL이 나왔는데 reward function이 단순히 discriminator의 형태로 구해지기 때문에 transferable, portable하지 않아서 transfer learning 측면에서는 좋지않은 성능을 보인다고 한다. 개인적으로 이 문제는 GAN구조의 mode collapsing 문제하고도 연관이 깊다고 생각이 든다. AIRL에서는 이 문제를 reward ambiguity problem이라고 하며 이 문제를 풀기 위해서는 dynamics가 변하더라도 optimal policy가 invariant 하도록하는 disentangle reward function을 찾아야 된다고 말한다. 기존의 reward함수에 next state를 추가적인 입력변수로 넣어서 dynamics의 변화를 reward함수에게 인지하도록 shaping term을 더하자는 것이 AIRL의 Intuition이었다. 그런데 단순히 state-only dependent한 reward만 구하는데 그치었다. action의 조그마한 변화에도 실패할 확률이 높아지게 되는 보행과제에 대해서는 state와 action모두 dependent한 reward함수를 찾아야 한다는 것이 EAIRL의 Motivation이다. 그것을 해결법으로 제시한 아이디어는 다음과 같다. 현재의 상태에서 agent가 어떠한 행동을 했을 때 다음 상태로 이동을 할 텐데 이때 학습에 미치는 영향력을 theoretical measure로 Empowerment라고 불리우는 mutual information으로 정량화하여 variational bound를 optimize하도록 하자는 것이다. 이로써 다음과 같은 두가지 효과를 보았다고 한다.
-
Empowerment 가 policy update에 대한 regularizer로 작용하여 expert demo에 overfitting하는 것을 막는다.
-
state-action에 dependent한 robust reward를 구한다.
- 기존의 maximum entropy inverse reinforcement learning 의 formulation에 empowerment regularization 기법을 도입하여 문제를 풀었다.
- expert demo로 overfitting되는 것을 막고 testing과 training상황이 조금 바뀌더라도 general하게 적용할수 있는 robust reward를 복원한다.
- robust 함은 empowerment 를 정의하여 학습했기 때문이라 했고, empowerment는 reward와 policy사이의 variation information이라고 한다. 그것을 internal reward로 하여 maximize하도록하여 학습한다.
2. Background
기존 MDP에서 추가되는 몇가지 Notation을 먼저 소개한다.
\[\begin{align} q(a\vert s, s') &: \mathcal{S} \times \mathcal{S} \times \mathcal{A} \rightarrow [0,1] \\ \Phi(s) &: \mathcal{S} \rightarrow \mathbb{R} \end{align}\]$q(a\vert s, s’)$ 는 inverse model로 현재 state에서 next state로 가기 위한 action의 분포를 의미한다.
$\Phi(s)$ 는 현재 state의 utility를 의미하며 empowerment based potential function으로 MaxEnt-IRL framework에서 policy를 업데이트를 regularize하기 위해 정의되었다.
두 함수는 mutual information을 maximize하기 위해서 variational lowerbound를 찾고 그것을 optimize해야하는데 그 과정의 일환으로 생겨난 function이라고 할 수 있다. 추 후 유도과정에서 두 함수가 생겨난 부분과 어떠한 의미를 지니는지 추가적으로 설명하겠다.
2.1 MaxEnt-IRL
이 부분에 대한 자세한 설명은 이전포스트를 참조하면 되겠지만 여기서는 간단히 설명하고 넘어가도록 하겠다.
MaxEnt-IRL은 Expert demonstration의 분포를 다음과 같이 energy function으로 근사된 reward함수로 표현된 boltzman distribution으로 모델링 하는 것으로 부터 출발한다.
\[p_{\xi}(\tau) = \frac{1}{Z} e^{r_{\xi}(\tau)}\]demonstration trajectory $\tau$ 는 optimal policy $\pi^{*}$ 로 부터 sampling 된 것이라고 가정한다. 위의 trajectory분포에 대한 likelihood를 최대화하는 것이 MaxEnt IRL의 목적함수가 된다. 하지만 continuous space에서 partition function $Z$을 구하는 것은 intractable하다. GCL에서는 $Z$ 를 구하기 위해서 proposal distribution 혹은 sampling policy 라고 불리우는 $q(a\vert s)$를 도입하여 importance sampling으로 근사해서 문제를 풀었다.
2.2 Adversarial Inverse Reinforcement Learning
GAIL에서는 reward 학습을 위한 IRL 과정과 policy 학습을 위한 RL과정 2단계로 이루어지던 학습과정을 1 step으로 reformulation해서 high dimensional problem 을 풀었다. IRL과정에서는 reward function을 neural net으로 근사하고 Apprenticeship Learning via IRL formulation에 opjective에 특수한 형태의 reward regularizer function을 추가한다. RL과정에서는 entropy term을 추가한. 두 과정을 composition하여 1step으로 유도한 결과 Jensen–Shannon divergence 를 최소화 한다는 것으로 relaxation 다음과 같이 할 수 있었다. 그 말은 곧 GAN 구조를 통해 효율적으로 학습할 수 있다는 것을 의미한다.
\[\underset{\pi}{\min} \underset{D \in (0,1)^{\mathcal{S} \times \mathcal{A}}}{\max} \mathbb{E}_{\pi} [\log D(s,a)] + \mathbb{E}_{\pi_{E}}[\log(1-D(s,a))] - \lambda H(\pi)\]위의 식에서 reward를 내포하고 있는 Discriminator는 단순히 Expert Policy와 학습하는 policy가 같은지 아닌지 binary classification하는 정도로 밖에 사용할 수 없어서 reward function을 복원할 수 없다. AIRL에서는 다음과 같이 reward함수를 복원할 수 있는 구조를 제안했다.
\[D_{\xi, \varphi}(s,a,s') = \frac{e^{f_{\xi, \varphi} (s,a,s')}}{e^{f_{\xi, \varphi} (s,a,s')} + \pi(a \vert s)} \;\; ,where \;\; f_{\xi, \varphi} (s,a,s') = r_{\xi}(s) + \gamma h_{\varphi}(s') - h_{\varphi} (s)\]policy는 다음과 같은 discriminative reward를 최대화하도록 학습된다.
\[\hat{r} = \log D(s,a,s') + \log(1-D(s,a,s'))\]reward shaping term $F = \gamma h_{\varphi}(s’) - h_{\varphi} (s)$ 에서 $h_{\varphi}(\cdot)$ 에는 어떠한 structure도 부과되지 않았기에 그 효과는 아직 모른다.
2.3 Empowerment as Maximal Mutual Information
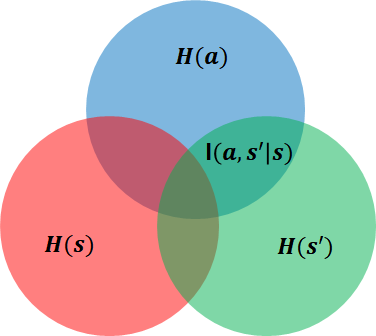
위의 information diagram에서 주어진 state에서 action과 next state에 대한 dependency관계를 Mutual Information으로 두고 measure하고 그것의 maximum 을 empowerment라고 부르고 internal reward로써 활용한다. empowerment는 직관적으로 현 상태에서 미래에 에이전트가 영향을 줄 수 있는 정도를 정량화 한 것이다. empowerment를 최대화 한다는 것은 에이전트가 영향을 줄 수 있는 정도를 강화하는 방향으로 학습해나가자는 말이다. agent가 도달가능한 상태의 수가 가장 많아지도록 강화하여 탐험을 강화한다는 것을 의미한다.
\[\begin{align} \Phi(s) &= \max I(a,s' \vert s) &\mbox{where } p(a,s' \vert s) = p(s' \vert a,s) w(a \vert s) \\ &= \max \mathbb{E}_{p(s' \vert a,s) w(a \vert s)} [\log (\frac{p(a,s' \vert s)}{w(a \vert s) p(s' \vert s)})] &\mbox{by mutual information definition} \\ \end{align}\]문제를 high dimensional space에서 tractable하게 풀기 위해서 Mutual information의 variational lowerbound를 찾아서 optimize해야한다. 이를 유도해보자. distribution over action $w(a\vert s)$ 와 Inverse model $q(a \vert s, s’)$ 로 VI를 표현하도록 유도해야한다.
\[\begin{align} I^{w,q}(s) &= H(a \vert s) - H(a \vert s', s) \\ &= H(a \vert s) + \mathbb{E}_{p(s' \vert a,s) w(a \vert s)} [\log p(a \vert s', s)]\\ &= H(a \vert s) + \mathbb{E}_{p(s' \vert a,s) w(a \vert s)} [\log \frac{p(a \vert s', s) q(a \vert s', s)}{q(a \vert s', s)}] \\ &= H(a \vert s) + \mathbb{E}_{p(s' \vert a,s) w(a \vert s)}[\log q(a \vert s', s)] + D_{KL}[p(a \vert s', s) \vert \vert q(a \vert s', s)]\\ &\geq H(a \vert s) + \mathbb{E}_{p(s' \vert a,s) w(a \vert s)}[\log q(a \vert s', s)] \\ &= - \mathbb{E}_{w(a \vert s)}[\log w(a \vert s)] + \mathbb{E}_{p(s' \vert a,s) w(a \vert s)}[\log q(a \vert s', s)] \end{align}\]위에서 구한 variational lowerbound 를 neural network로 parameterize 한 distribution over action $w_{\theta}(a \vert s)$ 와 Inverse model $q_{\phi}(a \vert s, s’)$ d에 대해서 maximize하는게 우리의 목적이다. 여기서 $w(a \vert s)$의 발산을 막기 위해서 $H(a \vert s)$ < $\eta$ 의 제약을 두어야 하는데 $\beta$ 는 $\eta$ dependent temperature term을 두어서 조절한다고 하는데 간결함을 위해 $\beta = 1$ 이라고 가정한다.
\[\begin{align} \Phi(s) &= \max I^{w,q}(a,s' \vert s) \\ &= - \mathbb{E}_{w(a \vert s)}[ \log w_{\theta}(a \vert s)] + \mathbb{E}_{p(s' \vert a,s) w(a \vert s)}[\log q_{\phi}(a \vert s', s)] \end{align}\]Empowerment를 $w_{\theta}(a\vert s)$ 와 $q_{\phi}(a \vert s, s’)$에 대해서 Expectation-Maximization(EM) 원리를 적용하여 학습한다. 간결함을 위해서 discrete state space와 discrete action space로 가정한다.
$q_{\phi}(a \vert s, s’)$ 는 supervised maximum log-likelihood problem을 풀고 $w_{\theta}(a\vert s)$ 는 $\frac{\partial I^{w,q}}{\partial w} = 0 \;\; s.t. \sum_{a} w(a\vert s)= 1$ 을 풀어서 구한다.
w에 대한 closed-form solution을 구하기 위해서 unconstrained form인 Lagrangian formulation으로 다시 쓰면 아래와 같다.
\[\begin{align} \hat{I^{w}}(s) &= \mathbb{E}_{p(s' \vert a,s) w(a \vert s)} [- \log w(a \vert s) + \log q(a \vert s', s)] + \lambda (\sum_{a}w(a \vert s) - 1) \\ &=\sum_{a}\sum_{s'} p(s' \vert a,s) w(a \vert s)[-\log w(a \vert s) + \log q(a \vert s', s)] + \lambda (\sum_{a}w(a \vert s) - 1) \\ &=-\sum_{a}\sum_{s'} p(s' \vert a,s)w(a \vert s)\log w(a \vert s) + \sum_{a} \sum_{s'} p(s' \vert a,s) w(a \vert s)\log q(a \vert s', s) + \lambda (\sum_{a}w(a \vert s) - 1) \end{align}\]$x \log x$ 를 $x$ 에 대해서 미분하면 $\log x +1$ 이고 $\sum_{s’}p(s’ \vert a, s) = 1$ 이기 때문에 다음과 같다.
\[\begin{align} \frac{\partial \hat{I}^{w,q}(s)}{\partial w} &= \sum_{a}\{(\lambda - 1) - \log w(a \vert s) + \mathbb{E}_{p(s'\vert a,s)} [\log q(a \vert s', s)] \} = 0 \\ w(a \vert s) &= e^{\lambda - 1} e^{\mathbb{E}_{p(s'\vert a,s)} [\log q(a \vert s', s)]} \end{align}\]$\sum_{a} w(a\vert s)= 1$ 라는 constraint를 사용하면, optimal solution은 다음과 같다.
\[\begin{align} w^{*}(a \vert s) &= \frac{1}{Z(s)} e^{u(s,a)} \\ &where \;\; u(s,a) = \mathbb{E}_{p(s'\vert a,s)} [\log q(a \vert s', s)] ,\;\; Z(s) = \sum_{a} u(s,a) \end{align}\]$\frac{\partial^{2} I^{w}(s)}{\partial^{2} w^{2}} = -\sum_{a} \frac{1}{w(a \vert s)} < 0$ 이기 때문에 solution은 maximum 이 된다.
위의 solution을 다시 간략화하면 다음과 같다.
\[u(s,a) = \log w^{*}(a \vert s) + \log Z(s)\]$w(a \vert s)$ 가 policy $\pi(a \vert s)$의 의미를 지니도록 하려면 $Z(s)$를 구하여 normalization 을 해야한다. $Z(s)$를 구하는것은 high dimensional space에서 Intractable하기 때문에 $\log Z(s)$ 를 empowerment based potential function $ \Phi(s)$ 로 두고 $w^{*}(a \vert s) \approx \log \pi(a \vert s) + \Phi(s)$ 로 근사를 하면
\[u(s,a) \approx \log \pi(a \vert s) + \Phi(s)\]라는 결론에 도달할 수 있다. 따라서 two approximation에 대한 Information loss 을 최소화하면 된다.
\[l_{I}(s,a,s') = \vert \log q_{\phi}(a \vert s', s) - (\log \pi_{\theta}(a \vert s) + \Phi_{\varphi})(s)\vert^{p}\]3. Empowered Adversarial Inverse Reinforcement Learning
이제 남은 일은 $l_q$ 와 $l_{I}$를 AIRL framework에 녹여내는 일이다. model은 다음과 같은 4가지로 구성된다.
-
Inverse Model : $q_{\phi}(a \vert s’, s)$
-
Empowerment based Potential Function : $\Phi_{\varphi}(s)$
reward-shaping function을 결정한다. $F = \gamma \Phi_{\varphi}(s’) - \Phi_{\varphi}(s)$
-
Reward Function : $r_{\xi}(s,a)$
-
Policy : $\pi_{\theta}(a \vert s)$
3.1 Inverse Model
maximum log-likelihood supervised learning problem을 푼다. inverse model의 predicted action과 policy generated trajectory $\tau = {s_{0}, a_{0} , \cdots, s_{T}, a_{T}} \sim \pi$ 사이의 mse를 최소화 한다.
\[l_{q} (s,a,s') = (q_{\phi}(\cdot \vert s, s') - a)^{2}\]3.2 Empowerment
$w^{*}(a \vert s)$ 에 대한 normalization term을 설명하며 아래와 같은 Information loss 를 최소화한다. 이는 곧 mutual information 을 최대화 하는 것을 의미한다.
\[l_{I}(s,a,s') = \vert \log q_{\phi}(a \vert s', s) - (\log \pi_{\theta}(a \vert s) + \Phi_{\varphi}(s))\vert^{p}\]3.3 Reward
Discriminator를 AIRL에서 했던 것과 유사하게 다음과 같이 구성한다.1
\[\begin{equation} D_{\xi, \varphi} (s,a, s') = \frac{e^{r_{\xi}(s,a) + \gamma \Phi_{\varphi'}(s') - \Phi_{\varphi}(s)}}{e^{r_{\xi}(s,a) + \gamma \Phi_{\varphi'}(s') - \Phi_{\varphi}(s)} + \pi_{\theta}(a \vert s)} \end{equation}\]학습을 안정화하기 위해서 n step마다 potential target을 업데이트 하는 stationary target을 적용한다.
Discriminator의 loss functions은 GAIL과 동일하게 expert trajectory $\tau_{E}$ 와 generated trajectory $\tau$ 사이의 binary logistic regression을 통해서 학습한다. 2
\[\mathbb{E}_{\tau} [\log D_{\xi, \varphi}(s,a,s')] + \mathbb{E}_{\tau_{E}} [1 - \log D_{\xi, \varphi}(s,a,s')]\]3.4 Policy
discriminative reward를 최대화 하면서 동시에 Information loss를 최소화하도록 설계되어야 한다.
discriminative reward는 다음과 같다.
\[\hat{r} (s,a,s') = \log D(s,a,s') - \log(1 - D(s,a,s'))\]이것을 policy gradient 식에 넣고 information loss term을 추가하면 된다.
\[\mathbb{E}_{\tau} [\log \pi_{\theta}(a \vert s) \hat{r}(s,a,s')] + \lambda_{I}\mathbb{E}[l_{I}(s,a,s')]\]$\tau_{E}$ 를 사용해서는 discriminator만 학습하는데 사용되지만 $\tau$ 는 모든 모델을 동시에 학습하는데 사용된다. Policy gradient의 predicted reward에 Information loss 를 포함시키도록 alternative reward $r_{\pi}(s,a,s’)$로 표현하면 효과적인 학습이 가능하다.
\[\mathbb{E}_{\tau} [\log \pi_{\theta}(a \vert s) r_{\pi}(s,a,s')]\]MaxEnt-RL의 목적함수는 학습하는 trajectory 분포와 energy based model로 근사화된 expert trajectory사이의 거리를 최소화하는 것으로 부터 출발한다.
\[\begin{align} - D_{KL}(\pi (\tau) || p_{\xi}(\tau)) &= \mathbb{E}_{\pi}[\log\frac{p_{\xi}(\tau)}{\pi (\tau)}] \\ &= \mathbb{E}_{\pi}[\log \frac{\frac{1}{Z} \cancel{p_(s_0)\overset{T-1}{\underset{t=0}{\Pi}} p(s_{t+1}|s_t, a_t)} e^{r_{\xi}(s_t,a_t)}} { \cancel{p_(s_0) \overset{T-1}{\underset{t=0}{\Pi}} p(s_{t+1}|s_t, a_t)} \pi(a_t| s_t)}] \\ &= \mathbb{E}_{\pi}[(\sum_{t=0}^{T-1} r_{\xi}(s_t, a_t) - \log \pi(a_t |s_t)) - \log Z(s_{t})] \end{align}\]위의 식에서 마지막 term은 $\pi$에 무관하므로 제외시키고 empowerment를 intrinsic reward로써 더하면 아래와 같은 식으로 policy의 목적함수가 구해진다. 3
\[\mathbb{E}_{\pi}[(\sum_{t=0}^{T-1} r_{\xi}(s_t, a_t) + \Phi(s_{t+1})- \log \pi(a_t |s_t))]\]이제 위의 식이 EAIRL에서 유도된 식과 equivalent함을 보이자.
$f(s,a,s’) = r(s,a) + \gamma \Phi(s’) - \Phi(s)$ 로 두고 1을 2 에 대입하면 다음과 같은 식이 나온다.
\[\begin{align} \hat{r} (s,a,s') &= \log D(s,a,s') - \log(1 - D(s,a,s')) \\ &= \log\frac{e^{f(s,a,s')}}{ \cancel{e^{f(s,a,s')} + \pi(a|s)}} - \log \frac{ \pi(a|s)}{\cancel{e^{f(s,a,s')} + \pi(a|s)}} \\ &= f(s,a,s') - \log \pi(a|s) \\ \end{align}\]위의 식에서 entropy regularization term 을 $\lambda_{h}$ 로 scale하고 Information loss term을 추가하여 $r_{\pi}(s,a,s’)$ 를 유도하면 다음과 같다.
간결함을 위해 $ \log q_{\phi}(a \vert s’, s) - (\log \pi_{\theta}(a \vert s) + \Phi_{\varphi})(s) > 0$ 라고 가정하고 유도를 진행한다.
\[\begin{align} r_{\pi}(s,a,s') &= f(s,a,s') - \lambda_{h}\log \pi(a|s) - l_{I}(s,a,s') \\ &= r(s,a) + \gamma \Phi(s') - \cancel{\Phi(s)} - \lambda_{h}\log \pi(a|s) - \log q(a \vert s', s) + \log \pi(a \vert s) + \cancel{\Phi(s)} \\ &= r(s,a) + \gamma \Phi(s') - \lambda_{h}\log \pi(a|s) - \log q(a \vert s', s) + \log \pi(a \vert s) \end{align}\]마지막 두 term을 $\lambda_{I}$ 로 scale하면 아래와 같은 결론이 나온다.
\[\begin{align} r_{\pi}(s,a,s') &= r(s,a) + \gamma \Phi(s') - \lambda_{h}\log \pi(a|s) - \lambda_{I}(\log q(a \vert s', s) -\log \pi(a \vert s)) \\ &= r(s,a) + \gamma \Phi(s') + \underbrace{(\lambda_{I} - \lambda_{h})\log \pi(a|s) - \lambda_{I}\log q(a \vert s', s)}_{\lambda\hat{H(\cdot)}} \end{align}\]아래와 같은 식으로 다시 표현할 수 있는데 이식은 $D_{KL}(\pi(\tau) \vert \vert p_{\xi}(\tau))$를 최소화하는 것으로 부터 유도된 entropy regularized policy update를 위한 reward 식에 empowerment term이 추가된 3과 일치한다는 것을 보인다.
\[r_{\pi}(s,a,s') = r(s,a) + \lambda_{I} \Phi(s') + \lambda\hat{H(\cdot)}\]Pseudo code

4. Result
Customize한 환경에서 Transfer learning 문제에 대한 reward learning 성능 비교가 있고 Benchmark에 대해서 비교한 policy learning 성능 비교 가 있다.
4.1 Reward Learning Performance
 |
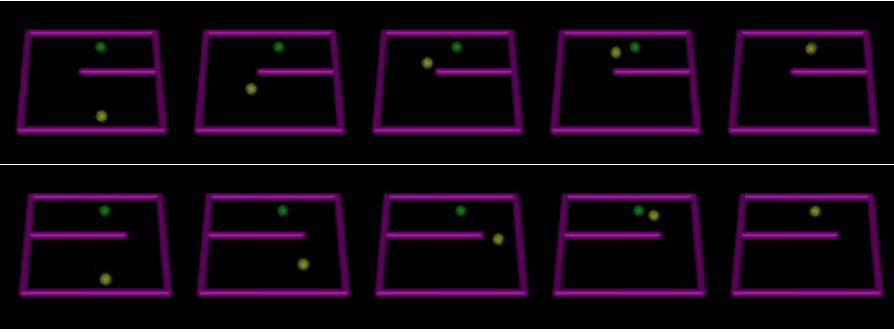 |
expert demo는 첫째 row에서 취득하고 두번째 row환경에서 성공적으로 학습을 성공했다고 한다.
성공적으로 state action에 둘다 dependent한 reward function을 복원할 수 있었고 성능면에서도 state of the art를 보여줬다.

Learning curve에서 보이듯이 expert에 가까운 성능을 보였고 sampling efficiency도 많은 향상을 보여준다.

4.2 Policy Learning Performance
bench mark task에 대해서도 최고 성능을 보였고 여기서 주목할 점은 오직 state에만 dependent한 reward 함수의 경우 보행 task같이 bad end가 자주일어나는 경우 성능이 크게 하락하는 것을 실험적으로 보였다.

5. Discussion
단순히 Expert demo와 Policy generated sample들 사이의 KL divergence를 최소화하는 것은 general reward function을 학습할 수 없었다.그래서 제안하는 논문에서는 empowerment를 통해 policy를 regularize함으로써 reward function에 robust함을 이끌어냈다.
AIRL도 state-only dependent disentangled reward function을 추구함으로써 robust함을 만들어 냈지만 action 에 대해서 independent한 것이 aggressive한 behavior를 만들어냈다.
real world application task인 autonomous driving, robot locomotion, manipulation task에서는 이러한 특성이 특히 중요했고 본 논문에서는 유의미한 결과를 만들어 냈다.
6. Conclusion and Future Work
variational information maximization을 통해서 empowerment를 학습하고 동시에 reward와 policy를 학습할수 있는 구조를 제안했다.
이러한 regularization 기법이 policy가 local behavior에 수렴하는 것을 막고 동시에 optimal한 reward를 복원할 수 있었다.
따라서 imitation learning과 transfer learning 문제 둘다 좋은 성능을 이끌어냈다.
future work로 single expert 가아닌 diverse expert에 의해서 생성된 demo로 부터 학습하는 쪽으로 진행을 할수도 있고, expert demo가 항상 optimal 이 아니고 optimal가 non-optimal behavior가 둘다 포함되어 있을 때 학습하는 방법을 연구하는 것도 흥미로울 것 같다.


Leave a comment