Reeds-Shepp (RS) Path

Reeds-Shepp Path

Introduction

지난 포스트에서 collision-free space에서 non-holonomic system을 가지고 있는 자동차의

운동 역학을 고려한 전진 경로를 생성하기 위해서 Dubin’s path 방법에 대해서 다루어 보았다.

단점을 후진을 모델링 하지 않아서 장애물을 고려하여 경로를 계획할 때

목적지까지 도달하지 못하는 경우가 발생하게 된다.

Reeds-Shepp Path 에서는 Dubin’s Path를 확장하여 reverse gear를 고려한다.

우선 Dubin’s Path를 리뷰해보면 모든 Optimal Forward Path를 다음과 같은 6가지의 class로 나눈다.

CSC (RSR, LSR, RSL, LSL) / CCC (LRL,RLR)

C는 circle 형태의 segment를 이고,

S는 Straight line segment를 의미한다.

R과 L 은 시계방향과 반시계방향을 의미한다.

여기서는 생성되는 Optimal Path의 group을 reverse gear를 고려했을 때 다음과 같은 9가지로 나눈다.

새로운 Symbol인 “$

$” 는 gear의 토글 여부를 의미한다.

각 Base word에 대해서 가능한 motion primitive sequence를 나열하면 다음과 같다.

총 48가지 조합이 존재하고 어떻게 저런 조합이 나왔는지는 이곳에서 자세히 나와있고 복잡하여 생략하겠다.

1년후에 HJ Sussman 및 G Tang 에서 사실 46가지면 ($L^{-}R^{+}L^{-}, R^{-}L^{+}R^{-}$ 제외) 충분하다고 증명되었고,

추후 8~9가지 함수를 중복으로 사용하여 구현되었다.

실제로 어떻게 적용하는지는 다음과 같다.

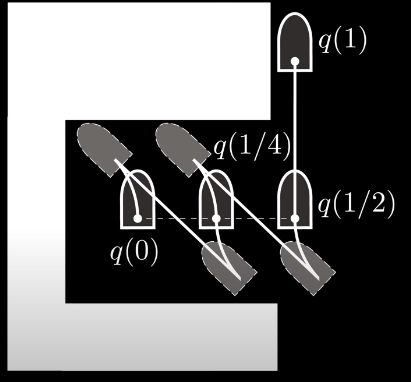
driving area 가 주어지고 $q_{0}$ 부터 $q_{1}$ 까지 경로를 만든다고 했을 때

feasible한 경로가 나오지 않을 수 있다.

이 경우 path의 segment를 $(q_{0}, q_{\frac{1}{2}}, q_{0})$ 로 분할하여 경로를 만든다.

만약 $(q_{0}, q_{\frac{1}{2}})$ 사이의 경로가 infeasible하다면

다시 $(q_{0}, q_{\frac{1}{4}}, q_{\frac{1}{2}})$ 로 분할하여 경로를 계획한다.

최종적으로 형성된 경로는 다음과 같을 것이다.

코드

PythonRobotics 에는 planning에 필요한 많은 모듈들이 구현되어 있어서

이곳에서 구현된 reeds_shepp_path_planning 코드를 분석해보려 했다.

그런데 이곳에는 논문에 존재하는 48가지의 모든 경우를 구현해놓지 않고 존재하지 않는 경우

SCS 경우가 들어있었다.

다행히도 모두 구현된 오픈소스를 발견했고 이 코드는 46가지 경우로 줄이고 함수도 12개를 중복을 사용하여

최적화 되어있지는 않지만 어찌됬든 잘 동작하기 때문에 이것을 분석해 보도록 하겠다.

def get_all_paths(start, end):
    """
    Return a list of all the paths from start to end generated by the
    12 functions and their variants
    """
    path_fns = [path1, path2, path3, path4, path5, path6, \
                path7, path8, path9, path10, path11, path12]
    paths = []

    # get coordinates of end in the set of axis where start is (0,0,0)
    x, y, theta = change_of_basis(start, end)

    for get_path in path_fns:
        # get the four variants for each path type, cf article
        paths.append(get_path(x, y, theta))
        paths.append(timeflip(get_path(-x, y, -theta)))
        paths.append(reflect(get_path(x, -y, -theta)))
        paths.append(reflect(timeflip(get_path(-x, -y, theta))))

    # remove path elements that have parameter 0
    for i in range(len(paths)):
        paths[i] = list(filter(lambda e: e.param != 0, paths[i]))

    # remove empty paths
    paths = list(filter(None, paths))

    return paths

우선 start와 end point 가 주어지면 change_of_basis 함수에서 local 좌표계로 바꾼다.

기어나 핸들의 반대로 하여 즉 timeflip과 reflect 총 $2^{2} = 4$ 가지 조합에 대해 경로들의 조합을 만들 수 있다.

$CSC $, $C\vert C_{\pi/2}SC $, 그리고 $ CSC_{\pi/2} \vert C $ 와 같이

두개의 C가 같은 경우와 다른 경우에 대해서 나뉘기 때문에

$9+3 = 12$가지 함수에 대해서 $12 \times 4 = 48$가지 후보 경로를 모두 생성할 수 있다.

최종적으로 각 sequence에 대해서 param 와 fesiblity를 체크하고 잔여 경로를 반환하면 된다.

모든 후보 경로 중 shortest path를 고르면 그것이 바로 최종적인 optimal path가 된다.

def timeflip(path):
    """
    timeflip transform described around the end of the article
    """
    new_path = [e.reverse_gear() for e in path]
    return new_path


def reflect(path):
    """
    reflect transform described around the end of the article
    """
    new_path = [e.reverse_steering() for e in path]
    return new_path

위와 같이 timefilp의 경우는 기어의 방향을 반대로 한것이다, 즉 +나 - 부호를 바꾼것이다.

이 경우 최종 목적지에 대해서 y측 대칭이동하고 방향의 부호를 바꾼다면

같은 함수로 동일한 목적지로 도달하는 경로의 shape을 얻을 수있다.

그리고 reflect경우는 핸들방향은 반대로 뒤집은 것이다, 즉 R이나 L의 기호를 바꾼 것이다.

이 경우 최종 목적지에 대해서 x축 대칭이동하고 방향의 부호를 바꾸면

마찬가지로 같은 함수로를 사용해서 동일 목적지로 달하는 경로의 shape을 얻을 수 있다.

약간 복잡할 수 있지만 조금만 생각해보면 알 수 있을 것이다.

CSC with same turns

def path1(x, y, phi):
    """
    Formula 8.1: CSC (same turns)
    """
    phi = deg2rad(phi)
    path = []

    u, t = R(x - math.sin(phi), y - 1 + math.cos(phi))
    v = M(phi - t)

    path.append(PathElement.create(t, Steering.LEFT, Gear.FORWARD))
    path.append(PathElement.create(u, Steering.STRAIGHT, Gear.FORWARD))
    path.append(PathElement.create(v, Steering.LEFT, Gear.FORWARD))

    return path

path 1은 csc base word에 대한 LSL 경로를 나타낸다.

목적지를 바꾸고 같은 함수를 호출하면 같은 row에 존재하는 조합을 얻을 수 있다.

R은 극좌표계로 바꾸는 함수이다.

u와 t는 극좌표계의 반지름과 각도를 나타낸다.

M은 각도를 $(-\pi/2, \pi/2)$ 범위로 바꾸는 함수이다.

최족 목적지에서 반지름이 1인 원(곡률)에 대해서 phi만큼 좌측으로 핸들을 돌리고 후진한 좌표를 극좌표계로 바꾼다.

그리고 최종목적지에 방향에 극좌표계의 각도를 빼면 최종적으로 얼만큼 회전할 것인지 각도가 나오게 된다.

t 만큼 회전하고 u만큼 직진하면 극좌표계의 위치로 간다.

이후 다시 v만큼 회전하면 최종적으로 $(x,y)$위치에서 $t+v=\pi$ 각도를 갖는 곳으로 이동하게 된다.

	@classmethod
    def create(cls, param: float, steering: Steering, gear: Gear):
        if param >= 0:
            return cls(param, steering, gear)
        else:
            return cls(-param, steering, gear).reverse_gear()

create함수로 가면 직진이든 회전이든

parameter=distance가 음수인 경우는 기어가 후진이니까 그렇게 처리를 했다는 것을 알 수 있다.

CSC with opposite turns

def path2(x, y, phi):
    """
    Formula 8.2: CSC (opposite turns)
    """
    phi = M(deg2rad(phi))
    path = []

    rho, t1 = R(x + math.sin(phi), y - 1 - math.cos(phi))

    if rho * rho >= 4:
        u = math.sqrt(rho * rho - 4)
        t = M(t1 + math.atan2(2, u))
        v = M(t - phi)

        path.append(PathElement.create(t, Steering.LEFT, Gear.FORWARD))
        path.append(PathElement.create(u, Steering.STRAIGHT, Gear.FORWARD))
        path.append(PathElement.create(v, Steering.RIGHT, Gear.FORWARD))

    return path

다음은 CSC중에서 반대방향 회전인 경우다.

이렇게 극좌표계와 회전 모델을 이용하여 각 segment의 타입별 이동거리를 구한다.

주어진 feasible 후보 경로들중 거리의 합이 최소입 optimal path를 선택하고

그리고 segement 별 interpolation을 통해서 좌표값들을 구하면 최종적으로 좌표값들을 구할 수 있다.

결과

Reference

Steven LaValle의 웹 페이지에서 수학적 증명

설명 영상

실행 영상

PythonRobotics