Linear and Non-Linear Least Squares Regression on Python

In [1]:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from copy import deepcopy

Least Squares

SSE(Sum of the Squared Error)을 최소화 하는 방법으로 해를 구한다.
Machine Learning 분야에서 주어진 데이터에 대해 목표하는 데이터를 예측 하기 위한 모델을 디자인할때 그 모델의 파라미터를 학습하는데 쓰인다.

In [2]:

# toy example
times = [0.10, 0.23, 0.36, 0.49, 0.61, 0.74, 0.87, 1]
quantities = [0.84, 0.30, 0.69, 0.45, 0.31, 0.09, -0.17, 0.12]
df = pd.DataFrame(data=[times, quantities])
df = df.T
df.columns = ['times', 'quantities']
data = df.to_numpy()
df

	times	quantities
0	0.10	0.84
1	0.23	0.30
2	0.36	0.69
3	0.49	0.45
4	0.61	0.31
5	0.74	0.09
6	0.87	-0.17
7	1.00	0.12

In [3]:

fig, ax = plt.subplots()
ax.scatter(data[:, 0], data[:, 1])
ax.set_xlabel('times')
ax.set_ylabel('qantities')
plt.show()

Linear Least Squares

모델을 선형함수로 디자인 한 경우를 말한다.
선형식으로 구성된 모델이므로 $Ax = b$의 관계를 가진다.

이를 이용하여 SSE를 최소화하는 모델의 파라미터를 직접적으로 바로 구할 수 있다.

Proof

주어진 값들을 이용하여 만든 matrix $\mathbf{X} \in \mathbb{R}^{m \times n}$,
찾고자하는 모델 파라미터 변수들을 $\mathbf{\boldsymbol{\beta}} \in \mathbb{R}^{n}$,
타겟 변수들을 $\mathbf{y} \in \mathbb{R}^{m}$
이라 두고, SSE 값 $S(\mathbf{\boldsymbol{\beta}})$ 는 다음과 같이 계산된다. \(\begin{align} S(\mathbf{\boldsymbol{\beta}}) &= \lVert \mathbf{y} - \mathbf{X} \mathbf{\boldsymbol{\beta}} \rVert^2 \\ &= (\mathbf{y} - \mathbf{X} \mathbf{\boldsymbol{\beta}})^\mathbf{T}(\mathbf{y} - \mathbf{X} \mathbf{\boldsymbol{\beta}}) \\ &= \mathbf{y}^{\mathbf{T}}\mathbf{y} - \mathbf{\boldsymbol{\beta}}^{\mathbf{T}} \mathbf{X}^{\mathbf{T}} \mathbf{y} - \mathbf{y}^{\mathbf{T}} \mathbf{X} \mathbf{\boldsymbol{\beta}} + \mathbf{\boldsymbol{\beta}}^{\mathbf{T}} \mathbf{X}^{\mathbf{T}} \mathbf{X} \mathbf{\boldsymbol{\beta}} \\ & (\mathbf{\boldsymbol{\beta}}^{\mathbf{T}} \mathbf{X}^{\mathbf{T}} \mathbf{y} = \mathbf{y}^{\mathbf{T}} \mathbf{X} \mathbf{\boldsymbol{\beta}} \because \text{it is scalar}) \\ &= \mathbf{y}^{\mathbf{T}} \mathbf{y} - 2 \mathbf{\boldsymbol{\beta}}^{\mathbf{T}} \mathbf{X}^{\mathbf{T}} \mathbf{y} + \mathbf{\boldsymbol{\beta}}^{\mathbf{T}} \mathbf{X}^{\mathbf{T}} \mathbf{X} \mathbf{\boldsymbol{\beta}} \\ \end{align}\)

$S(\boldsymbol{\beta})$ 를 최소화하는 $\boldsymbol{\beta}$를 찾으면 된다.
이 방식을 쓸때, $S(\boldsymbol{\beta})$ 가 최솟값을 가지기 위해서 $\mathbf{X}^{\mathbf{T}} \mathbf{X}$ 는 positive definite이어야 한다.
positive definite일때 다음과 같은 특징을 가진다.

• $\mathbf{X}^{\mathbf{T}} \mathbf{X}$의 모든 eigen value 값들이 양의 실수
• $\mathbf{X}$의 rank는 $n$(full column rank)

why?

[5]를 참고하면 자세히 알수 있다.
한마디로 말하면 우리의 목표 함수인 SSE가 극소값을 가질 조건을 의미.

추가적인 성질로 symmetrix matrix 관련하여 다음과 같은 특성들이 있다.
($\mathbf{X}^{\mathbf{T}} \mathbf{X}$ 는 symmetric matrix임.)

• 모든 element가 실수인 symmetic 인 matrix $\Rightarrow$ positive definite
• eigen decomposition했을때 diagonalizable 함.($n$ 개의 서로 orthogonal한 eigen vector를 갖는다.)

따라서, 정리하면 다음과 같이 전개된다. \(\begin{align} \frac{\partial S(\boldsymbol{\beta})}{\partial \boldsymbol{\beta}} &= 0 \\ -2 \mathbf{X}^{\mathbf{T}} \mathbf{y} + 2 \mathbf{X}^{\mathbf{T}} \mathbf{X} \boldsymbol{\beta} &= 0 \\ \mathbf{X}^{\mathbf{T}} \mathbf{X} \boldsymbol{\beta} & = \mathbf{X}^{\mathbf{T}} \mathbf{y} \\ \boldsymbol{\beta} & = (\mathbf{X}^{\mathbf{T}} \mathbf{X})^{-1}\mathbf{X}^{\mathbf{T}} \mathbf{y} \\ \end{align}\)

다시 문제로 되돌아가자.
아래 식과 같이 linear 모델을 가정하고, $\beta_1, \beta_2$ 를 찾으면 된다.

\[\begin{align} q(t) &= \beta_1 t + \beta_2 \\ &= \begin{bmatrix} t & 1 \end{bmatrix} \begin{bmatrix} \beta_1 \\ \beta_2 \\ \end{bmatrix} \\ \mathbf{y} &= \mathbf{X} \boldsymbol{\beta} \end{align}\]

In [4]:

t = data[:, 0]
X = np.concatenate((t[:, np.newaxis], 
                    np.ones(len(data))[:, np.newaxis]), axis=1)
print(X)
np.matmul(X.T, X) # symmetric 

[[0.1  1.  ]
 [0.23 1.  ]
 [0.36 1.  ]
 [0.49 1.  ]
 [0.61 1.  ]
 [0.74 1.  ]
 [0.87 1.  ]
 [1.   1.  ]]

array([[3.1092, 4.4   ],
       [4.4   , 8.    ]])

In [5]:

y = data[:, 1] # quantities
pseudo_inv = np.matmul(np.linalg.inv(np.matmul(X.T, X)), X.T)
ans = np.matmul(pseudo_inv, y)
print("estimated beta={}".format(ans))
SSE = sum((y - (ans[0] * t + ans[1])) ** 2)
print("minimized SSE={}".format(SSE))

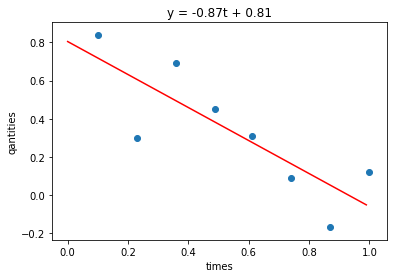
estimated beta=[-0.86593151  0.80501233]
minimized SSE=0.24029957196749854

Visualization

In [6]:

t = np.arange(0, 1, 0.01)
pred = ans[0] * t + ans[1]

fig, ax = plt.subplots()
ax.scatter(data[:, 0], data[:, 1])
ax.set_xlabel('times')
ax.set_ylabel('qantities')
ax.set_title(label='y = {:.2f}t + {:.2f}'.format(ans[0], ans[1]))
ax.plot(t, pred, color='red')
plt.show()

Non-Linear Least Squares

모델을 비선형 함수로 디자인 한 경우
$f(x) = b$ 관계를 갖는다.
Newton-Gauss method를 사용하면 모델 파라미터에 대한 선형화된 Recurrence를 찾을 수 있다.
이 Recurrence에 linear least square방식을 이용하여 모델의 파라미터를 업데이트 함으로써 수치해석적으로 오차를 최소화하는 모델 파라미터 값들을 찾는다.

비선형 함수 $f(\boldsymbol{\beta} \vert \mathbf{x})$는 주어진 데이터 $\mathbf{x}$를 이용하여 타겟 변수 $y$를 예측하는 함수이다.
이 예측에 대한 SSE $S(\mathbf{\boldsymbol{\beta}})$는 다음과 같으며 이를 최소화하는 모델 파라미터를 찾을 것이다.

\[\begin{align} S(\boldsymbol{\beta}) &= \lVert f(\boldsymbol{\beta} \vert \mathbf{x}) - \mathbf{y}\rVert^2 \\ &= \sum_{i=1}^{m}{(f(\boldsymbol{\beta} \vert x_i) - y_i)^2} \end{align}\]

이 objective 함수를 최소화하는 $\boldsymbol{\beta}$ 를 찾을 것이다. 따라서, 아래의 연립 방정식을 풀면 된다.

\[\begin{cases} f(\boldsymbol{\beta} \vert x_1) - y_1 = 0 \\ f(\boldsymbol{\beta} \vert x_2) - y_2 = 0 \\ ... \\ f(\boldsymbol{\beta} \vert x_m) - y_m = 0 \\ \end{cases}\]

위와같이 $n$개의 $\boldsymbol{\beta} = [\beta_1, \beta_2, …, \beta_n]$ 에 대해 $m$개의 비선형 연립 방정식에 대한 해를 구하는 문제가 있을때, 이를 수치해석적으로 구하는 Gauss-Newton 방법이 있다. 관련 블로그 글

$f(\boldsymbol{\beta} \vert \mathbf{x}) - \mathbf{y} = 0$의 근사 해 $\boldsymbol{\beta}$를 구하자.
( Newton-Rapshon method으로 생각하면 현재 위치에서 접선과 \beta 축이 만나는 지점으로 업데이트 해나가는 방식이다.Tayler급수로도 생각가능, 편의상 $f(\boldsymbol{\beta} \vert \mathbf{x})$ 를 $f(\boldsymbol{\beta}$) 로 표기)

\[\begin{align} \mathbf{y} = J_{f(\boldsymbol{\beta_k})} (\boldsymbol{\beta_{k + 1}} - \boldsymbol{\beta_{k}}) + f(\boldsymbol{\beta_k})\\ J_{f(\boldsymbol{\beta_k})} (\boldsymbol{\beta_{k + 1}} - \boldsymbol{\beta_{k}}) = \mathbf{y} - f(\boldsymbol{\beta_k}) \end{align}\]

위의 결과를 보면 $Ax=b$ 꼴의 선형적인 관계로 생각할 수 있다.
($J_{f(\boldsymbol{\beta_k})} \in \mathbb{R}^{m \times n}, f(\boldsymbol{\beta_k}) \in \mathbb{R}^{m}, \boldsymbol{\beta_k} \in \mathbb{R}^{n}$, $k$는 iteration index)

따라서, linear least square 방법을 이용하여 $\boldsymbol{\beta}$ 에 대한 Recurrence는 다음과 같이 유도된다.

\[\begin{align} J_{f(\boldsymbol{\beta_k})}^{\mathbf{T}} J_{f(\boldsymbol{\beta_k})} (\boldsymbol{\beta_{k + 1}} - \boldsymbol{\beta_{k}}) &= J_{f(\boldsymbol{\beta_k})}^{\mathbf{T}}(\mathbf{y} - f(\boldsymbol{\beta_k})) \\ \boldsymbol{\beta_{k + 1}} - \boldsymbol{\beta_{k}} &= (J_{f(\boldsymbol{\beta_k})}^{\mathbf{T}} J_{f(\boldsymbol{\beta_k})})^{-1} J_{f(\boldsymbol{\beta_k})}^{\mathbf{T}}(\mathbf{y} - f(\boldsymbol{\beta_k})) \\ \end{align}\]

여기서 $J_{f(\boldsymbol{\beta_k})}$ 는 다음과 같은 matrix 이다. \(\begin{bmatrix} \frac{\partial f(\boldsymbol{\beta} \vert x_1)}{\partial{\beta_1}} & \frac{\partial f(\boldsymbol{\beta} \vert x_1)}{\partial{\beta_2}} & ... & \frac{\partial f(\boldsymbol{\beta} \vert x_1)}{\partial{\beta_n}} \\ \frac{\partial f(\boldsymbol{\beta} \vert x_2)}{\partial{\beta_1}} & \frac{\partial f(\boldsymbol{\beta} \vert x_2)}{\partial{\beta_2}} & ... & \frac{\partial f(\boldsymbol{\beta} \vert x_2)}{\partial{\beta_n}} \\ ... & ... & ... & ... \\ \frac{\partial f(\boldsymbol{\beta} \vert x_m)}{\partial{\beta_1}} & \frac{\partial f(\boldsymbol{\beta} \vert x_m)}{\partial{\beta_2}} & ... & \frac{\partial f(\boldsymbol{\beta} \vert x_m)}{\partial{\beta_n}} \\ \end{bmatrix}\)

$(J_{f(\boldsymbol{\beta_k})}^{\mathbf{T}} J_{f(\boldsymbol{\beta_k})})^{-1}J_{f(\boldsymbol{\beta_k})}^{\mathbf{T}}(\mathbf{y} - f(\boldsymbol{\beta_k}))$ 가 수렴할 때까지 Recurrence 수행한다.

문제로 되돌아가서, 다음과 같은 비선형 모델을 정의하자.

\[\begin{align} q(t) &= \beta_2 e^{\beta_1 t} \\ \mathbf{y} &= f(\boldsymbol{\beta} \vert \mathbf{x}) \end{align}\]

In [7]:

t = data[:, 0]
q = data[:, 1]

In [8]:

def f(beta, t):
    """ return target value(shape=[m]) given beta and t.
    Args: 
        beta: shape=[n=2]
        t: shape=[m]"""
    return beta[1] * np.exp(beta[0] * t)

init = np.array([1.5, 2])  # initial states of beta
beta = deepcopy(init)
fbeta = f(beta, t)
print(fbeta.shape)
fbeta

(8,)

array([2.32366849, 2.82397984, 3.43201372, 4.17096399, 4.9935505 ,
       6.06871679, 7.37537819, 8.96337814])

Implementation of Gradient and Jacobian Numerically

In [9]:

def gradient(f, beta, epsilon=1e-7):
    """ numerically find gradients for beta. 
    beta: shape=[n] """
    grad = np.zeros_like(beta, dtype=float)
    for i in range(len(beta)):
        h = np.zeros_like(beta, dtype=float)
        h[i] = epsilon
        grad[i] = (f(beta + h) - f(beta - h)) / (2 * h[i])
    return grad

def jacobian(f, beta, t, epsilon=1e-7, verbose=False):
    """ numerically find jacobian matrix, of shape=[m, n]
    f: function, kinds of m
    beta: shape=[n] """
    m, n = len(t), len(beta)
    jaco = np.zeros(shape=(m, n), dtype=float)
    for i in range(m):
        jaco[i, :] = gradient(lambda e: f(e, t=t[i]), beta)
    return jaco

In [10]:

J = jacobian(f, beta, t)
print(J.shape)
J

(8, 2)

array([[0.23236685, 1.16183424],
       [0.64951536, 1.41198992],
       [1.23552494, 1.71600686],
       [2.04377235, 2.08548199],
       [3.0460658 , 2.49677525],
       [4.49085042, 3.0343584 ],
       [6.41657903, 3.68768909],
       [8.96337815, 4.48168906]])

First Iteration Line by Line

In [11]:

np.matmul(J.T, J)

array([[157.14028051,  92.63511433],
       [ 92.63511433,  59.76329427]])

In [12]:

pseudo_inv = np.matmul(np.linalg.inv(np.matmul(J.T, J)), J.T)
print(pseudo_inv.shape)
pseudo_inv

(2, 8)

array([[-0.11573418, -0.11356496, -0.10509634, -0.08771619, -0.06080097,
        -0.01568001,  0.05168969,  0.14879718],
       [ 0.19883246,  0.19965588,  0.19161624,  0.17085875,  0.13602128,
         0.07507748, -0.01841585, -0.15564996]])

In [13]:

diff = q - fbeta
print(diff.shape)
diff

(8,)

array([-1.48366849, -2.52397984, -2.74201372, -3.72096399, -4.6835505 ,
       -5.97871679, -7.54537819, -8.84337814])

In [14]:

update = np.matmul(pseudo_inv, diff)
print(update.shape)
update

(2,)

array([-0.25446605, -1.53060605])

In [15]:

beta = beta + update
beta

array([1.24553395, 0.46939395])

Overall Iteration

In [16]:

def newton(f, init, x, y, epsilon=1e-7, verbose=False, history=False):
    """ Newton Raphson Method.
    f: functions, functions can be different m functions by x(depends on given dataset) 
    init: np.array, of shape=[n], initial state of beta(model parameters) 
    x: np.array, of shape=[m, p=1], given dataset 
    y: target dataset, of shape=[m] """
    m, n = len(x), len(init)
    beta = deepcopy(init)
    bound = 1e-7
    memo = [beta]
    while True:
        J = jacobian(f, beta, x)  # [m, n]
        pseudo_inv = np.matmul(np.linalg.inv(np.matmul(J.T, J)), J.T)  # [n, m]
        fbeta = f(beta, x) # [m]
        diff = y - fbeta  # [m]
        update = np.matmul(pseudo_inv, diff)
        beta = beta + update
        if bound > sum(np.abs(update)):
            break
        if verbose: print("beta={} update={}".format(beta, sum(np.abs(update))))            
        if history: memo.append(beta)
    if not history: return beta
    return beta, np.array(list(zip(*memo)))

In [17]:

print(t) # given dataset
print(q) # target

[0.1  0.23 0.36 0.49 0.61 0.74 0.87 1.  ]
[ 0.84  0.3   0.69  0.45  0.31  0.09 -0.17  0.12]

In [18]:

init = np.array([1.5, 2])
ans, history = newton(f, init, x=t, y=q, verbose=True, history=True)
print("estimated beta={}".format(ans))
SSE = sum((q - f(beta, t)) ** 2)
print("minimized SSE={}".format(SSE))

beta=[1.24553395 0.46939395] update=1.7850720976449588
beta=[0.02047755 0.52811626] update=1.283778713511213
beta=[-1.61271204  0.80096624] update=1.9060395771269723
beta=[-2.46726249  1.01216871] update=1.0657529124230951
beta=[-2.4021815   1.00898294] update=0.0682667564238679
beta=[-2.41576988  1.01216461] update=0.016770051170741707
beta=[-2.41322039  1.01153913] update=0.003174974435458694
beta=[-2.41370391  1.01165805] update=0.0006024458740083727
beta=[-2.41361238  1.01163555] update=0.00011402799420298648
beta=[-2.41362971  1.01163981] update=2.1587509853843168e-05
beta=[-2.41362644  1.011639  ] update=4.079957196284623e-06
beta=[-2.41362705  1.01163916] update=7.649656799668669e-07
beta=[-2.41362694  1.01163913] update=1.3763927009247112e-07
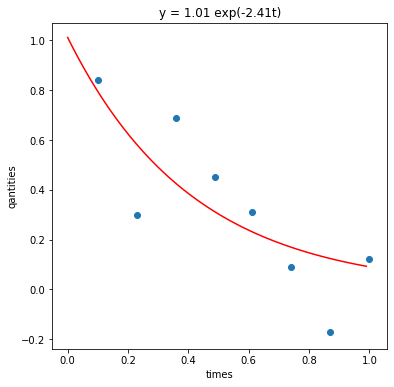
estimated beta=[-2.41362696  1.01163913]
minimized SSE=6.7511665453525165

Visualization

In [19]:

fig, ax = plt.subplots(figsize=(6, 6))
t = np.arange(0, 1, 0.01)
pred = f(ans, t)
ax.scatter(data[:, 0], data[:, 1])
ax.set_xlabel('times')
ax.set_ylabel('qantities')
ax.plot(t, pred, color='red')
ax.set_title(label='y = {:.2f} exp({:.2f}t)'.format(ans[1], ans[0]))
plt.show()

Reference

[1] Least Squares - wiki
[2] Proofs involving ordinary least squares - wiki
[3] Linear Algebra Korean tutorial
[4] Linear/Non-Linear Least Squares Slide English tutorial
[5] Positive Definite Meaning Korean
[6] Non-Linear Least Squares - wiki